Множество – первичное неопределяемое понятие. Обозначают множества большими латинскими буквами A, B, C, X, …. Под множеством понимают совокупность (группу, набор и т.д.) элементов, которые характеризуются одинаковыми свойствами.
Множества изображают диаграммами (кругами) Эйлера-Венна (рис.1).

Рис. 1
Если элемент а принадлежит множеству А, то пишут a Î A; если элемент а не принадлежит множеству А, то пишут a Ï A.
Множество может задаваться с указанием его характеристического свойства. Например, если A состоит из элементов x, для которых выполняется свойство P(x), то пишут  .
.
Если каждый элемент множества A есть элемент множества B, то множество A называется подмножеством множества B (или говорят, что A включено в B), пишут A Ì B (или B É A) (рис. 2). Два множества A, B называются равными (A = B), если они состоят из одних и тех же элементов: A = B тогда и только тогда, когда A Ì B и B Ì A. Множество, которое не имеет элементов, называется пустым и обозначается Æ.
К основным операциям над множествами относят пересечение, объединение, разность, дополнение.
Пересечением множеств A, B называется множество A Ç B, состоящее из всех тех элементов, которые принадлежат и множеству A и множеству B (рис. 3).
Объединением множеств A, B называется множество A È B, состоящее из всех тех элементов, которые принадлежат или множеству A, или множеству B (хотя бы одному из множеств A, B) (рис. 4).
Разностью множеств A \ B называется множество, состоящее из всех тех элементов, которые принадлежат множеству A и не принадлежат множеству B (рис. 5).
Дополнением множества A до конкретного (универсального) множества U называется множество  , которое определяется равенством
, которое определяется равенством 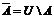 (рис. 6).
(рис. 6).



A Ì B A Ç B A È B
Рис. 2 Рис.3 Рис.4



Рис. 5 Рис. 6
Для произвольных множеств A, B, C справедливы свойства:
1)  коммутативность объединения;
коммутативность объединения;
2)  коммутативность пересечения;
коммутативность пересечения;
3)  ассоциативность объединения;
ассоциативность объединения;
4)  ассоциативность пересечения;
ассоциативность пересечения;
5)  ,
, 
дистрибутивность;
6)  ;
;
7)  ;
;
8) 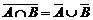 ;
;
9)  .
.
Пусть  – количество элементов множеств А и В соответственно, тогда справедлива формула
– количество элементов множеств А и В соответственно, тогда справедлива формула
 (8)
(8)
Рассматривают следующие числовые множества.
 множество натуральных чисел.
множество натуральных чисел.
 множество целых чисел.
множество целых чисел.
Q – множество рациональных чисел: это множество всех обыкновенных дробей, т.е. чисел вида 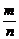 , где
, где  .
.
Множество Q определяется также, как множество всех бесконечных десятичных периодических дробей.
I – множество иррациональных чисел: это множество всех бесконечных десятичных непериодических дробей.
R – множество действительных чисел:  .
.
Верны соотношения:
 ,
,  ,
, 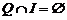 .
.
Произведение первых n натуральных чисел называется факториалом, для него введен специальный символ:
 .
.
По определению принимают 0! = 1.
Для всякого 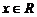 определены следующие понятия:
определены следующие понятия:
 целая часть (антье) числа x, определяется как целое число такое, что
целая часть (антье) числа x, определяется как целое число такое, что
 ;
;
 дробная часть (мантисса), определяется равенством
дробная часть (мантисса), определяется равенством
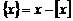 ;
;
 знак числа (сигнум), определяется следующим образом:
знак числа (сигнум), определяется следующим образом:

Если  некоторые действительные числа, то сумму этих величин обозначают с использованием знака суммы:
некоторые действительные числа, то сумму этих величин обозначают с использованием знака суммы:
 ,
,
где k – индекс суммирования.
Свойства суммы:
1) 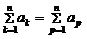 – сумма не зависит от того, какой буквой обозначен индекс суммирования;
– сумма не зависит от того, какой буквой обозначен индекс суммирования;
2)  ;
;
3) 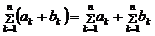 ;
;
4)  – свойство сдвига индекса суммирования.
– свойство сдвига индекса суммирования.
Пример 1. Доказать равенство
 (9)
(9)
Доказательство. Пусть  . Согласно определению разности, получаем
. Согласно определению разности, получаем  и
и  . Поскольку выполняются оба эти условия, то это возможно только в случае
. Поскольку выполняются оба эти условия, то это возможно только в случае  . Получаем, что
. Получаем, что  и
и  , т.е.
, т.е.  . Этим мы доказали, что
. Этим мы доказали, что
 . (10)
. (10)
Допустим, что  . Тогда
. Тогда  и
и  , но это означает, что
, но это означает, что  .
.
Два условия  и
и  , которые имеют место, означают, что
, которые имеют место, означают, что  , т.е.
, т.е.
 . (11)
. (11)
Равенство (9) доказано, поскольку установлена справедливость включений (10) и (11).
Пример 2. На первом курсе учатся 200 студентов. Из них своевременно сдали зачет по математике 175 человек, а по физике – 185 человек. Не сдали зачет ни по математике, ни по физике 10 человек. Сколько студентов сдали оба зачета?
Решение. Пусть A – множество всех студентов курса; B – множество студентов, которые сдали зачет по математике, C – по физике (рис.7).

Рис. 7
Согласно условию задачи,  ,
,  ,
,  ,
,  и надо найти
и надо найти  .
.
Находим, сколько человек сдали хотя бы один зачет:
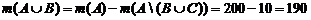 .
.
Используем далее формулу (8), из которой выражаем
 .
.
Получаем
 .
.
Ответ: 170 человек.
Пример 3. Сократить дробь
 .
.
Решение. Выделим общий множитель в числителе и в знаменателе. Очевидно, что
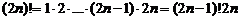 ;
;
 .
.
Поэтому
 .
.
Пример 4. Вычислить сумму
 .
.
Решение. Получим последовательно слагаемые, придавая  :
:

Вычисляя, приходим к ответу
 .
.
Задания
I уровень
1.1. Пусть  ,
,  ,
,  . Найдите множество:
. Найдите множество:
1) A È B; 2) A Ç B; 3) B È C; 4) B Ç C;
5) (A È B) Ç C; 6) A È (B Ç C); 7) A / (B Ç C).
1.2.Пусть А – множество натуральных делителей числа 15; В – множество простых чисел, меньших 10; С – множество четных чисел, меньших 9. Найдите множество:
1) A È B; 2) A Ç B; 3) B Ç C;
4) (A È C) Ç B; 5) A È (C Ç B); 6) A Ç B Ç C.
1.3. В группе учатся 28 студентов, каждый из которых умеет кататься на лыжах или коньках. При этом 20 человек умеют кататься на лыжах, 15 человек – на коньках. Определите, сколько студентов умеют кататься и на коньках, и на лыжах?
Ответ: 7.
1.4. Задано некоторое количество натуральных чисел, которые кратны или числу 2 или числу 3. Известно, что числу 2 кратны 10 чисел; числу 3 кратны 7 чисел; и числу 2 и числу 3 кратны 4 числа. Определите общее количество заданных чисел.
Ответ: 13.
1.5. Все 25 человек класса сходили в театр или кино. Известно, что 20 человек были в кино, 10 человек – и в театре, и в кино. Сколько человек было в театре?
Ответ: 15.
1.6. Вычислите:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 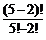 .
.
1.7. Сократите дробь:
1)  ; 2)
; 2)  .
.
1.8. Определите целую и дробную части числа:
1) 1,02; 2) –1,2; 3)  ;
;
4)  ; 5) –5,2; 6) 3,25.
; 5) –5,2; 6) 3,25.
1.9. Вычислите:
1)  ; 2)
; 2)  .
.
1.10. Запишите сумму, указав каждое слагаемое, и вычислите ее:
1) 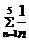 ; 2)
; 2)  ; 3)
; 3)  .
.
II уровень
2.1. Запишите, с помощью каких операций над множествами A, B, C получено заштрихованное множество на рис.8:
1) 2) 3)



4) 5) 6)



Рис. 8
2.2. Пусть  – подмножества универсального множества U = R. Найдите множество:
– подмножества универсального множества U = R. Найдите множество:
1) 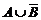 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
2.3. Заданы множества 
 ,
,  . Найдите множество:
. Найдите множество:
1) A È B; 2) A Ç B; 3) B / C;
4) A / B; 5) A Ç B Ç C; 6) A È B È C.
2.4. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на лыжах, и на коньках?
Ответ: 862.
2.5. В группе из 100 туристов 70 человек знают английский, 45 французский и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?
2.6. В штучном отделе магазина посетители обычно покупают любо один торт, либо одну коробку конфет, либо один торт и коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
Ответ: 81.
2.7. В первом туре олимпиады участвовали 100 студентов, из них 70 человек получили право участвовать во втором туре олимпиады по физике, 45 – по математике. Известно, что 23 человека могут участвовать во втором туре и по физике и по математике. Сколько студентов не допущено ко второму туру ни по физике ни по математике?
2.8. Сравните дроби:
1)  и
и  ;
;
2)  и
и  .
.
2.9. Сократите дробь и упростите полученное выражение:
1)  ; 2)
; 2)  ;
;
3) 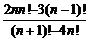 ; 4)
; 4)  .
.
III уровень
3.1. Для универсального множества R рассматриваются подмножества 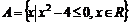 ,
,  . Найдите множество:
. Найдите множество:
1)  ; 2)
; 2)  ; 3)
; 3) 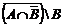 .
.
3.2. Докажите включение:
1)  ;
;
2)  .
.
3.3. Докажите равенство:
1)  ;
;
2)  .
.
3.4. Среди абитуриентов, которые успешно выдержали вступительные экзамены в университет, отметку «отлично» получили: по математике – 48 человек; по физике – 37; по белорусскому языку – 42; по математике или физике – 75; по математике или белорусскому языку – 76; по физике или белорусскому языку – 66; по всем трем дисциплинам – 4. Выясните: 1) сколько абитуриентов получили хотя бы одну пятерку; 2) сколько человек получили только одну пятерку.
3.5. В школьной олимпиаде по математике участвовали 100 человек, по физике – 50, по информатике – 48. Когда учеников опросили, в скольких олимпиадах они участвовали, ответ «в двух» дали вдвое меньше человек, чем «в одной», а «в трех» - втрое меньше, чем «в одной». Сколько всего учеников участвовало в этих олимпиадах?
Ответ: 121.
3.6. В олимпиаде по математике принимало участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну – по геометрии и одну – по тригонометрии. Результаты проверки работ представлены в таблице:
.
| Решены задачи | Количество решивших |
| по алгебре | |
| по геометрии | |
| по тригонометрии | |
| по алгебре и геометрии | |
| по алгебре и тригонометрии | |
| по геометрии и тригонометрии |
Известно также, что три человека не справились ни с одной задачей. Сколько учащихся решили все три задачи? Сколько решили ровно две задачи?
3.7. Из ста абитуриентов на первом экзамене получили отличные и хорошие оценки 80%, на втором экзамене – 72%, на третьем – 60%. Какое может быть наименьшее число абитуриентов, получивших отличные и хорошие оценки на всех трех экзаменах?
3.8. Выясните, при каком натуральном  справедливо неравенство и докажите его методом математической индукции:
справедливо неравенство и докажите его методом математической индукции:
1)  ; 2)
; 2) 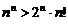 ; 3)
; 3) 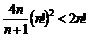 .
.