Порядок выполнения домашней контрольной работы

Студент выполняет тот вариант контрольной работы, который совпадает с порядковым номером по списку группы.

Таблица 1

Номер варианта	Номера задач

 

Таблица 2

Номер варианта	Номера задач

Решение задач типового варианта контрольной работы

Задание 1. Даны комплексные числа ż₁= -2 + ί и ż₂= 3 + ί.

Найти: 1) ż₁ + ż₂ 2) ż₂ - ż₁ 3) ż₁ * ż₂ 4) ż₁ / ż₂

Решение

1) ż₁ + ż₂ = -2 + ί + 3 + ί = (-2+3) + ί (1+1) = 1+2ί

2) ż₂ - ż₁ = 3 + ί – (- 2 + ί) = (3-(-2)) + ί (1-1) = 5+0ί = 5

3) Перемножим числа ż₁ и ż₂:

ż₁ ∙ ż₂ = (-2 + ί) ∙ (3 + ί) = (-2∙3-1∙1)+(-2∙1+3∙1)ί = -7 + ί

4) Для нахождения частного умножим числитель и знаменатель дроби на 3 – ί (т.е. на число, сопряженное знаменателю). Тогда получим:

ί, т.к. ί ² = -1

 

Задание 2. Дана система линейных уравнений.

х + 5у – z = 3,

2x + 4y -3z = 2,

3x – y – 3z = -7.

Проверить, совместна ли эта система, и в случае совместимости решить ее:

а. методом Гаусса;

б. методом Крамера;

Решение

Совместность данной системы проверим по теоре­ме Кронекера-Капелли. С помощью элементарных преобразований найдем ранг матрицы

А

 

данной системы и ранг расширенной матрицы

Для этого умножим первую строку матрицы В на -2 и сложим со второй, затем умножим первую строку на -3 и сложим с третьей. Поменяем местами второй и третий столбцы. Получим

В = ~ ~

Следовательно, гаng А = гаng В = 3 (т е. числу неизвестных систем). Значит, исходная система совместна и имеет единственное ре­шение.

А. Методом Гаусса.

х + 5у – z = 3,

2x + 4y -3z = 2,

3x – y – 3z = -7.

Составим матрицу из коэффициентов при неизвестных и свободных членов:

А

(вертикальной чертой отделен столбец, составленный из свободных членов).

Умножая первую строку матрицы А поочередно на -2, -3 и прибавляя соответственно ко второй и третьей, получаем матрицу

1 5 -1 3

А₁ = 0 -6 -1 -4

0 -16 0 -16

Матрице А₁ соответствует система уравнений

х + 5у – z = 3,

- 6y -3z = - 4,

- 16y = -16.

Из третьего уравнения находим у = 1, второе уравнение дает z = 4 – 6y, т.е. z = -2,

а первое х = 3 – 5у + z, т.е. х = - 4.

Следовательно, исходная система также имеет решение.

х = - 4; у = 1; z = - 2

Ответ: (-4; 1; -2)

Б. Методом Крамера.

где:

∆ = = - 16

 

∆_х = = 64

 

∆_у = = -16

 

∆_z = = 32

Находим: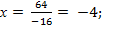

Ответ: (-4; 1; -2)

Задание 3. Найти пределы:

а) 5х² + 13х + 6 б) 7х⁴ + 2х³ +5

lim -------------------- lim --------------------

x → - 2 3х² + 2х – 8 x → ∞ 6х⁴ + 3х³ – 7x

Решение

а) Здесь имеем неопределенность . Для того чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель (х+2). В результате получим:

5х² + 13х +6 5(x+2)(x+3/5) 5(x+3/5)

lim -------------------- = lim -------------------- = lim -------------------- =

x→ -2 3х² + 2х – 8 x→ -2 3(x+2)(x-4/3) x→ -2 3(x-4/3)

 

5x + 3 5∙(-2) + 3 -7

= lim ----------- = ---------------- = ---- = 0,7

x→ -2 3x - 4 3∙ (-2) - 4 -10

 

б) 7х⁴ + 2х³ +5

lim --------------------

x→ ∞ 6х⁴ + 3х³ – 7x

Здесь имеем неопределенность . Чтобы раскрыть это неопределенность, разделим числитель и знаменатель на старшую степень многочленов в числителе и знаменателе, т.е. на х⁴

Тогда получим:

7х⁴ + 2х³ +5 7 + 2/х +5/х⁴ 7

lim -------------------- = lim -------------------- = ----

x→ ∞ 6х⁴ + 3х³ – 7x x→ ∞ 6 + 3/х² – 7/x³ 6

 

так как 2/х, 5/х⁴, 3/х², 7/х³ → 0 при x → ∞.

 

Задание 4. Исследовать функцию y = x³ – 3x² + 1 и построить ее график.

Решение.

1. Область определения х? (- ∞; + ∞); функция непрерывна во всей области определения.

2. Находим производную функции
у' = Зх² - 6х,

приравниваем ее к нулю и определяем критические точки (по­дозрительные на экстремум)

Зх² - 6х = 0;

Зх (х-2) = 0; х₁ = 0, х₂ = 2

 

3. Исследуем функцию на монотонность и экстремум и построим таблицу 1.

Область определения разделится на промежутки (-∞; 0), (0; 2) и (2: +∞). Определим знак производной на каждом промежутке. Имеем у (-1) = 3∙ (-1)² = - 6 (-1) = 9 > 0,

у' (1) = 3 • 1² - 6 •1 = -3 < 0, у' (3) = 3 • 3²-6 • 3 = 27 -18=9>0. Значит, в промежутках (-∞; 0), (2; +∞) функция возрастает, а в промежутке (0; 2) - убывает. Функция имеет максимум при х = 0, у (0) = 0³ - 3 • 0² + 1 = 1, а при х = 2 - минимум

у (2) = 2³ - 3 • 2² + 1 = -3.

Имеем (0; 1) -точка максимума, (2;-3) - точка минимума.

 

4. Исследуем функцию на интервалы выпуклости и точки перегиба и составим таблицу 2.

Для нахождения участков выпуклости и вогнутости точек пере­гиба найдем вторую производную.

у" =(Зх²-6х)' = 6х - 6

6х - 6 = 0; х = 1. Крайняя точка II рода (подозрительна на перегиб).

Определим знаки второй производной слева и справа от точки х = 1. Например, при х = 0, у" (0) = - 6 < 0; при х = 2. у" (2) = 6 • 2 - 6 = 6 > 0. Следовательно, в промежутке (-∞; 1) кривая выпуклая, а в промежутке (1; +∞) - вогнута. При х = 1 имеем точку перегиба, ее ор­дината у (1)= 1³ -3 • 1² + 1 = -1.

Точка (1; -1) - точка перегиба.

5. Вертикальных асимптот у графика нет, т.к. нет точек разрыва функции.

Ищем наклонные асимптоты в виде у=kx+b.

 

k = lim = lim = lim (x² - 3x + ) = ∞

x→∞ x→∞ x →∞

т.е. не существует конечного предела вида lim = k,

x→∞

то график данной функции асимпотот не имеет.

6. Для уточнения графика функции найдем координаты еще двух точек, абсциссы которых равны - 1 и 3:

У(-1) = (-1)³-3∙(-1)²+1 = - 3

У(3) = 3³-3 - 3²+1 = 1

(-1; -3); (3; 1) - дополнительные точки.

Строим все найденные точки и соединяем их плавной линией (рис. 1).

 

Задание 5. Найти y’

a) y = + -5

Применяя формулы ( n· 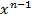, (u(x) ± v(x))’=u’(x) ± v’(x), находим:

y’ = ( + 8x^-1 – 5x⁷ + 10x^-6)’ = (x^9/4)’ + 8(x^-1)’ – 5 (x⁷)’ + 10(x^-6)’ = x^5/4 – 8x² – 35x⁶ – 60x⁷ =

= 2,25x · - -35x⁶ - .

 

b) y = (x³ – 4x² +6)·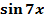

Применяя формулы ( n· (u(x) · v(x))’=u’(x) · v(x) + u(x) · v’(x), и формулу дифференцирования сложной функции, имеем:

y’= (x³ – 4x² + 6)’ + (x³ – 4x² + 6) = (3x² – 8x) + 7(x³ – 4x² + +6) .

c) y = =

Применяя формулы ()’ = ; ( n· ;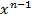

(u ± v)’=u’ ± v’, получим:

y’ = = =

= =

d) y = tg2x

y’ = (ln(x+4))’ tg2x + ln (x+4) (tg2x)’= ·tg2x + ln(x+4)· = + =

=

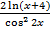e) y =

y’ = (cos 3x)’·ctg (x⁴) + cos 3x·(ctg (x⁴))’= - 3sin 3x · ctg x⁴ – 4x³ · cos 3x

 

Задание 6. Найти полный дифференциал функции Z = 2x² у ³.

Решение. Находим частные производные данной функции:

ð Z ð Z

---- = 4xy³, ---- = 6x² y³,

ð x ð y

Умножая частные производные на дифференциалы соответст­вующих аргументов, получим частные дифференциалы функции:

d_xZ = 4xy³ dx; d_yZ = 6x²y² dy.

Искомый полный дифференциал функций найдем как сумму ее частных дифференциалов:

dZ = 4xy³ dx + 6x²y² dy.

Задание 7. Найти неопределенные интегралы и результат про­верить дифференцированием.

a) ∫ b) ∫ x² lnx dx

= ∫

обозначим через t = 2 – 3x2 найдем dt = d (2 – 3x2) = (2 – 3x2) dx = = - 6xdx; отсюда следует xdx = - 1/6 dt

Решение.

a) ∫

= - ∫ t ^-1/2 dt = - + C = - + C = - + C = - +C

ПРОВЕРКА:

(- 1/3 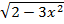)’ = (- 1/3 )^1/2)’ = - 1/3 ∙ 1/2 (2-3x²)^-1/2 ∙ (- 3 ∙ 2x) =

= - 1/6 ∙(- 6x) ∙ =

 

б) Применим формулу интегрирования по частям:

∫ UdV = U ∙ V - ∫ VdU

Пусть U = lnx, тогда dU= dx / x

dV = x² dx, V = ∫ x² dx = x³ /3

Имеем ∫ x² lnx dx = lnx ∙ x³ /3 - ∫ x³ /3 ∙ dx / x = 1/3 x³ lnx - 1/3 ∫ x² dx = 1/3 x³ lnx - 1/3 ∙ x³/3 + C = 1/9 x³ (3 lnx – 1) + C

ПРОВЕРКА:

(1/9 x³ (3 lnx – 1))’ = 1/9 (x³)’ (3 lnx – 1) + 1/9 x³ (3 lnx – 1)’ = 1/9 ∙ 3x² (3 lnx – 1) + 1/9 x³ (3/x) =

= x² lnx – 1/3 x² + 1/3 x² = x² lnx

 

Задание 8. Найти площадь фигуры, ограниченной линиями у = 1/4 (х - 2)² и х + 2у – 14= 0; сделать чертеж.

Решение. Площадь фигуры, ограниченной сверху непрерыв­ной кривой

у = f(х), снизу непрерывной кривой у = φ (х), слева - пря­мой х = а и справа - прямой х = в, вычисляется по формуле:

S =

Определим точки пересечения данных линий, для чего решим систему:

Из второго уравнения у = 7 - х/2 подставим значения в первое уравнение системы вместо у разность 7 - х/2, получим:

7-х/2 = 1/4(х-2)²;

7-х/2= 1/4(х²-4х + 4);

28 - 2х = х² - 4х + 4;

х² - 2х - 24 = 0,

откуда x₁ = - 4, х₂ = 6; у₁ = 9, у₂ = 4.

Таким образом, линии пересекаются в точках А (-4; 9) и В (6; 4). Построим чертеж (рис. 3).

Искомая площадь:

S = 7 - x/2 – ¼ (x - 2)²) dx =

- 4

= 7 - 1/2x – 1/4 x² + x - 1) dx =

= 6 + 1/2 x - 1/4 x²) dx = (6x + 1/4 x² – 1/12 x³) = (36 + 9 – 18) – (- 24 + 4 + 16/3) =

= 41 2/3 (кв. ед.)

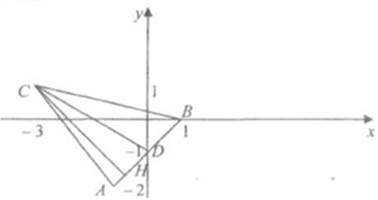
Задание 9. Дан треугольник с вершинами А(-1,- 2), В(1, 0), С(-3,1). Найти:

1) уравнение стороны АВ;

2) уравнение медианы CD;

3) уравнение высоты CH;

4) угол между прямыми СD и СН.

Решение.

 

1) При составлении уравнения стороны АВ воспользуемся урав­нением прямой, проходящей через 2 точки - М₁(х₁,у₁) и М₂(х₂,у₂):

=

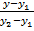
Подставив в данное уравнение координаты точек А и В, получим

x + 1 у + 2 x + 1 у + 2

----- - = ----- или ------- = ---------, х + 1 = у + 2,

1 + 1 0+2 2 2

y = x-1 - уравнение стороны АВ с угловым коэффициентом k_AB=1

2) Точка В является серединой отрезка АВ, её координаты найдём по формулам:

= = 0, = = -1

Итак, D(0,-1).

Уравнение прямой, проходящей через точки С и D имеет вид:

x + 3 у - 1 2

----- - = ------ или - — (x + 3) = y - 1,

0 + 3 -1 - 1 3

у = - x - 1 - уравнение прямой СD, угловой коэффициент k_CD = -

3) Поскольку прямая СH перпендикулярна прямой АB, угловые ко­эффициенты этих прямых связаны соотношением k_CH = - = -1

Для написания уравнения прямой СН воспользуемся уравнением: y – y₀ = k(x-x₀)

Полагая в этом уравнении х₀ = -3, у₀ =1, k=k_сн = -1, полу­чим уравнение:

у -1 = -1(х + 3) или y = -х - 2

уравнение высоты СН, угловой коэффициент k_CH= -1.

4) Угол между прямыми СD и СH найдётся по формуле:

tg = = = =

= arctg ≈ 12⁰