Нормальные напряжения в т. 1 шва № 1:
 ,
,
где  – момент сопротивления поперечного сечения шва;
– момент сопротивления поперечного сечения шва;
 ,
,
 МПа.
МПа.
По условию прочности это напряжение не должно превышать допускаемого нормального для сварного шва  МПа. Так как
МПа. Так как  , то прочность в т. 1 сечения шва № 1 удовлетворительная.
, то прочность в т. 1 сечения шва № 1 удовлетворительная.
В т. 2 шва № 1 действуют нормальные и касательные напряжения, поэтому для оценки прочности в этой точке необходимо определить эквивалентные напряжения:
 ,
,  ,
,  ,
,
где  – максимальный статический момент отсеченной части сечения шва;
– максимальный статический момент отсеченной части сечения шва;
 – момент инерции сечения шва.
– момент инерции сечения шва.
 МПа,
МПа,
 мм3,
мм3,
 мм4,
мм4,
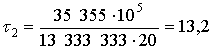 МПа,
МПа,
 МПа
МПа  .
.
Таким образом, прочность шва № 1 удовлетворительная.
Производим проверочный расчет угловых швов № 2. Сварные швы № 2 воспринимают следующие нагрузки:
– продольную силу  Н,
Н,
– поперечную нагрузку  Н,
Н,
– изгибающий момент  Н×мм.
Н×мм.
Эпюры напряжений от перечисленных нагрузок в расчетном сечении швов №2 будут иметь следующий вид:
 ,
,  ,
,  .
.
где  – осевой момент инерции контура швов в сечении II – II.
– осевой момент инерции контура швов в сечении II – II.

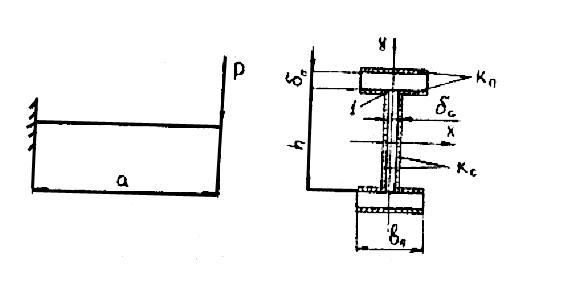
Направление действия касательных напряжений показано на рисунке:

Как видно из эпюр касательных напряжений, в угловых швах наиболее нагруженными точками являются периферийные т. 1. Напряжение в т. 1 от продольной нагрузки
 МПа,
МПа,
от поперечной нагрузки –
 МПа,
МПа,
от изгибающего момента –
 ,
,  ,
,
 МПа.
МПа.
Определяем результирующее напряжение в т. 1 углового шва:
 МПа
МПа  .
.
Следовательно, прочность сварных швов № 2 неудовлетворительная. Для снижения действующих в них расчетных напряжений и повышения несущей способности швов необходимо увеличить катет.
Задача 6. Консоль двутаврового сечения приварена к колонне угловыми швами по всему контуру своего сечения и нагружена силой  , как показано ниже на рисунке Конструкция изготовлена из стали Ст. 3, швы выполнены ручной дуговой сваркой электродами обыкновенного качества Э42. Определить катеты швов, приваривающих полку и стенку.
, как показано ниже на рисунке Конструкция изготовлена из стали Ст. 3, швы выполнены ручной дуговой сваркой электродами обыкновенного качества Э42. Определить катеты швов, приваривающих полку и стенку.  МПа,
МПа,  МПа,
МПа,  кН,
кН,  мм,
мм,  мм,
мм,  мм,
мм,  мм,
мм, 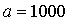 мм.
мм.
Решение
Определяем действующие нагрузки на угловые швы. В плоскости присоединения действуют:
– поперечная нагрузка 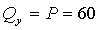 кН,
кН,
– изгибающий момент  Н×мм.
Н×мм.
Катеты швов определяем из системы уравнений:
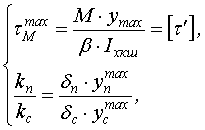
 .
.
Пренебрегая слагаемыми, содержащими  ,
,  и т. д., получаем
и т. д., получаем
 ,
,
 мм4,
мм4,

Решая последнюю систему уравнений, находим  мм,
мм,  мм.
мм.
Так как при расчете угловых швов не учитывалась поперечная нагрузка, которую по условной методике расчета воспринимают только вертикальные швы, производим проверку выбранных швов по расчетным напряжениям в т. 1 (см. рис. выше). В этой точке действуют касательные напряжения от момента  и от поперечной нагрузки
и от поперечной нагрузки  :
:
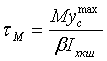 ,
,

 МПа,
МПа,
 МПа.
МПа.
Так как напряжения действуют во взаимно перпендикулярных направлениях, то результирующее напряжение
 МПа
МПа  .
.
Результирующее напряжение в т. 1 углового шва, приваривающего стенку, не превышает допускаемого  , следовательно, прочность выбранных швов удовлетворительная.
, следовательно, прочность выбранных швов удовлетворительная.
Задача 7. Решить предыдущую задачу из условия, обеспечивающего равнопрочность сварных швов и основного металла двутавра.
Решение
При решении этой задачи считаем, что нагрузка  на консоль двутаврового сечения не известна. Величина этой нагрузки является предельно допустимой для основного металла двутавра с учетом схемы нагружения и допускаемых напряжений
на консоль двутаврового сечения не известна. Величина этой нагрузки является предельно допустимой для основного металла двутавра с учетом схемы нагружения и допускаемых напряжений  и
и  .
.

Предельно допускаемую нагрузку определяем из условия прочности в опасных точка 1, 2 и 3 сечения двутавра.
В т. 1 действуют максимальные нормальные напряжения от изгибающего момента (см. эпюры напряжений).
 ,
,  ,
,  ,
,
 ,
,
 мм4.
мм4.
 Н.
Н.
В т. 2 действуют нормальные напряжения от изгибающего момента, величина которых несколько ниже, чем в т. 1, однако в т. 2 действуют еще касательные напряжения от поперечной нагрузки, определяемые по формуле Журавского. Прочность в т. 2 оцениваем по эквивалентным напряжениям:
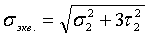 ,
,  ,
,
где  – ордината точки 2;
– ордината точки 2;
 ,
,
 – статический момент отсеченной части сечения (в данном случае - полки),
– статический момент отсеченной части сечения (в данном случае - полки),
 – толщина сечения двутавра в месте отсечения.
– толщина сечения двутавра в месте отсечения.
Согласно схеме нагружения консоли  и
и  .
.
 мм3,
мм3,
 ,
,
 ,
,
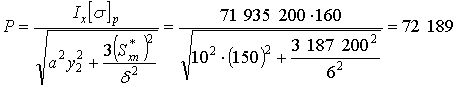 Н.
Н.
В т. 3 действуют только касательные напряжения, однако величина их наибольшая (см. эпюры напряжений).
 ,
,
 мм3,
мм3,
 Н.
Н.
Таким образом, наименьшую нагрузку P по условию прочности допускает т. 1, следовательно, предельно допускаемую нагрузку на консоль определяем
из условия прочности в т. 1, т. е.  Н. Далее задача решается так же, как и задача 6. Пользуясь приведенной в этой задаче программой, находим
Н. Далее задача решается так же, как и задача 6. Пользуясь приведенной в этой задаче программой, находим  мм,
мм,  мм.
мм.
Задача 8. Определить величину предельной нагрузки  , приложенной к кронштейну (см. рис.) под углом
, приложенной к кронштейну (см. рис.) под углом  к его оси. Кронштейн к соединяемому элементу конструкции приварен внахлестку угловым швом по всему контуру присоединения. Материал кронштейна – сталь Ст. 3, сварка произведена вручную электродами обыкновенного качества,
к его оси. Кронштейн к соединяемому элементу конструкции приварен внахлестку угловым швом по всему контуру присоединения. Материал кронштейна – сталь Ст. 3, сварка произведена вручную электродами обыкновенного качества,  мм,
мм,  мм,
мм, 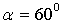 ,
,  мм,
мм, 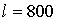 мм,
мм,  МПа.
МПа.

Решение
Определяем координату центра тяжести контура швов  :
:
 ,
,
 мм.
мм.
Определяем действующие нагрузки в центре тяжести контура сварных швов:
 ;
;
 ;
;
 .
.
Расчет сварных швов производим методом осевого момента инерции. Согласно этому методу, напряжения в отдельных точках угловых швов от момента, действующего в плоскости контура сварных швов, пропорциональны расстоянию до этих точек от оси  . Поэтому максимальные напряжения от момента определяются по следующей формуле:
. Поэтому максимальные напряжения от момента определяются по следующей формуле:
 ,
,

 МПа.
МПа.
Напряжения в швах от продольной силы
 МПа.
МПа.
Напряжения в швах от поперечной нагрузки
 МПа.
МПа.
Так как напряжения от продольной нагрузки и момента действуют в одном направлении, а напряжения от поперечной силы им перпендикулярны, то результирующее напряжение

Результирующее напряжение не должно превышать допускаемого напряжения на срез для сварного шва  . Определяем величину предельной нагрузки
. Определяем величину предельной нагрузки  на сварные швы:
на сварные швы:
 Н.
Н.
Задача 9. Две пластины из стали Ст. 3 сварены встык ручной дуговой сваркой электродом Э42. Определить допустимое усилие на сварное соединение при статической нагрузке; при переменной нагрузке, когда усилие  изменяется от
изменяется от  до
до  .
.

Решение
Для стали Ст. 3  МПа, при ручной дуговой сварке электродами обыкновенного качества Э42
МПа, при ручной дуговой сварке электродами обыкновенного качества Э42  МПа.
МПа.
При статической нагрузке допустимое усилие на сварной шов
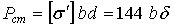 .
.
При динамической нагрузке допустимое усилие на сварной шов определяется по следующей формуле:
 ,
,
в околошовной зоне
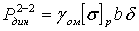 .
.
Коэффициент уменьшения допускаемого напряжения при расчете на усталость
 ,
,
где  и
и  – коэффициенты, устанавливаемые нормами проектирования;
– коэффициенты, устанавливаемые нормами проектирования;
 –эффективный коэффициент концентрации напряжений;
–эффективный коэффициент концентрации напряжений;
 – характеристика цикла нагружения.
– характеристика цикла нагружения.
 .
.
По табл. 10.10 [1, с. 240] принимаем  ,
,  . Эффективный коэффициент концентрации напряжений
. Эффективный коэффициент концентрации напряжений  , определяем по табл. 1010.11
, определяем по табл. 1010.11
[1, с. 240–242]. Для шва  , для основного металла
, для основного металла  .
.
Так как по условию задачи  , а среднее напряжение /усилие/ цикла нагружения больше нуля, то коэффициенты
, а среднее напряжение /усилие/ цикла нагружения больше нуля, то коэффициенты
 ,
,
 ,
,
 ,
,
 .
.
Основной материал, прилегающий к сварному шву, оказался более чувствительной зоной к динамическим нагрузкам, поэтому допустимое усилие на сварное соединение  .
.
Задача 10. В раскосе фермы действует переменное усилие, изменяющееся от  кН до
кН до  кН. Раскос состоит из двух швеллеров, подобрать их сечение и рассчитать присоединение швеллера к косынке фермы одним лобовым и двумя фланговыми швами. Ферма изготовлена из стали 15ХСНД, швы сварены вручную электродами Э50.
кН. Раскос состоит из двух швеллеров, подобрать их сечение и рассчитать присоединение швеллера к косынке фермы одним лобовым и двумя фланговыми швами. Ферма изготовлена из стали 15ХСНД, швы сварены вручную электродами Э50.

Решение
В прил. 8 [2, с. 324] находим  МПа. Так как сварка ручная электродом обыкновенного качества, то
МПа. Так как сварка ручная электродом обыкновенного качества, то
 МПа
МПа  .
.
Определяем характеристику цикла нагружения:
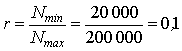 .
.
По прил. 7 [2, с. 319–323] определяем, что  максимален в местах перехода от фланговых швов к основному металлу и равен
максимален в местах перехода от фланговых швов к основному металлу и равен  , принимаем
, принимаем  ,
,  .
.

Так как на одни швеллер действует максимальная нагрузка 200 кН, требуемое сечение швеллера
 мм2.
мм2.
По прил. 2 [2, с. 305–312] выбираем швеллер № 24а ( мм,
мм,  мм,
мм,  мм).
мм).
Определяем размеры швов.
Эффективные коэффициенты концентрации напряжений по расчетным сечениям сварных швов.
для лобового шва 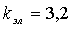 ,
,
для фланговых швов  .
.
 ,
,

 .
.
Для ручной дуговой сварки  . Принимая,
. Принимая,  мм,
мм,
 мм,
мм,  мм, получаем:
мм, получаем:
 мм.
мм.
Задача 11. С помощью линий влияния определить изгибающий момент и поперечную нагрузку в сечениях A, B и C балки.

Решение
1. Построение линий влияния  и
и  :
:


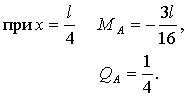


2. Построение линий влияния  и
и 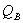 :
:

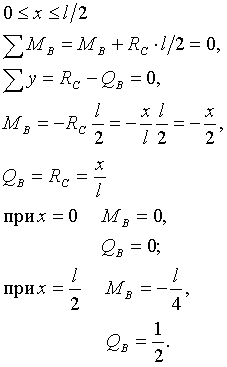
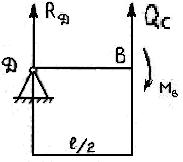
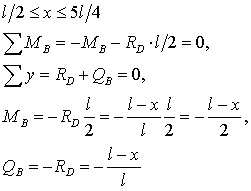

3. Построение линий влияния  и
и 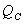 :
:

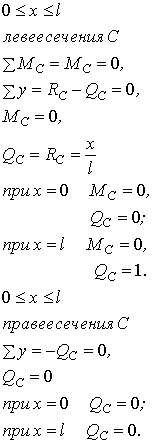

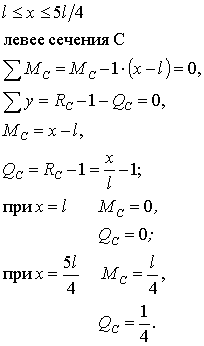



4. Определение величины действующих нагрузок в сечениях A, B и C балки.
Величину действующих нагрузок по известным линиям влияния можно определить по формуле  или
или  ,
,
где  или
или  – действующий в сечении момент или сила;
– действующий в сечении момент или сила;
 – сосредоточенные силы;
– сосредоточенные силы;
 – интенсивность распределения нагрузки;
– интенсивность распределения нагрузки;
 – ордината соответствующей линии влияния (
– ордината соответствующей линии влияния ( или
или  ) под сосредоточенной нагрузкой;
) под сосредоточенной нагрузкой;
 – алгебраическая сумма площадей под соответствующей линией влияния на длине действия распределенной нагрузки.
– алгебраическая сумма площадей под соответствующей линией влияния на длине действия распределенной нагрузки.
Определяем
 ,
,
 ,
,
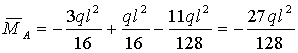 .
.
Определяем
 ,
,
 ,
,
 .
.
Определяем
 ,
,
 ,
,
 .
.
Определяем  . Так как в сечении А приложена сосредоточенная сила, то величина действующей поперечной нагрузки в этом сечении неопределенна (изменяется скачком). Поэтому определенной является поперечная нагрузка левее сечения А и правее сечения А. Разность между этими поперечными нагрузками должна быть равна по величине сосредоточенной силе:
. Так как в сечении А приложена сосредоточенная сила, то величина действующей поперечной нагрузки в этом сечении неопределенна (изменяется скачком). Поэтому определенной является поперечная нагрузка левее сечения А и правее сечения А. Разность между этими поперечными нагрузками должна быть равна по величине сосредоточенной силе:
 ,
,
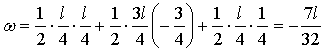 ,
,
 .
.
 ,
,
 ,
,
 ,
,
 .
.
Определяем
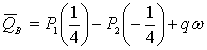 ,
,
 ,
,
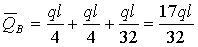 .
.
Определяем  . В сечении С приложена сосредоточенная сила – реакция опоры С. Поэтому в сечении С так же, как и в сечении А, определяем два значения поперечной нагрузки: одно левее точки С, а другое правее. Разность между этими поперечными нагрузками должна быть равна реакции опоры:
. В сечении С приложена сосредоточенная сила – реакция опоры С. Поэтому в сечении С так же, как и в сечении А, определяем два значения поперечной нагрузки: одно левее точки С, а другое правее. Разность между этими поперечными нагрузками должна быть равна реакции опоры:
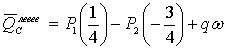 ,
,
 ,
,
 ,
,
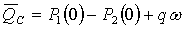 ,
,
 ,
,
 ,
,
 .
.
Задача 12. С помощью линий влияния определить экстремальные нагрузки в стержнях 1–2 и 1–3 фермы,  м,
м, 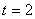 мм,
мм, 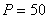 кН,
кН,  кН.
кН.

Решение
Для определения экстремальных усилий в стержнях 1 – 2 и 1 – 3 фермы строим линии влияния продольных усилий в этих стержнях, единичную нагрузку при этом перемещаем по нижнему поясу фермы, т. е. по тому, где приложены реальные нагрузки  и
и  .
.
Строим линию влиянии продольных усилий в стержне 1 – 2:
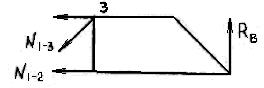




Строим линию влияния продольных усилий в стержне 1–3:


Располагаем подвижную нагрузку  в наиболее невыгодное положение над соответствующей линией влияния и определяем экстремальные значения усилий
в наиболее невыгодное положение над соответствующей линией влияния и определяем экстремальные значения усилий  и
и  :
:
 ;
;
 кН;
кН;
 ;
;
 кН;
кН;
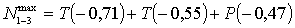 ;
;
 кН;
кН;
 ;
;
 кН.
кН.