лоран дифференциальный рикатти уравнение
При решении дифференциальных уравнений степенными рядами каждый полученный ряд является только элементом искомого решения, определенным в его области сходимости. Область сходимости степенного ряда есть круг, на границе которого должна находиться по крайней мере одна особая точка решения исходного дифференциального уравнения. Поэтому для того, чтобы распространить полученные результаты на всю комплексную область, нам прежде всего надо найти 'методику исследования поведения решений в окрестности полюса и существенно особой точки, которые на практике встречаются наиболее часто. С этой целью обратимся к характерному примеру, рассматривая при этом искомую функцию w = и +iv и аргумент z =x+iy как комплексные величины.
Пример. Определим все полюсы решения задачи Коши для уравнения Риккати
(5.1)
Решение. Представим исходное уравнение в виде:
(5.2)
Тогда для определения коэффициентов его решения
(5.3)
рекуррентная формула будет иметь следующий вид:
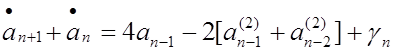
или
(5.4)
Значение коэффициентов gn для заданной функции
находим, представив ее в виде ряда с тем же центром z0= 0.
При n= 0 мы должны положить
a-1=0; a-1(2)=a-2(2)=0; a*0=0 (так как a*n=nan); g0 = - 1,
и тогда, согласно формулам (5.4), находим
a*1=g0=-1; a1=a*1
При n=1 имеем:
и, следовательно,
Вычисление остальных коэффициентов a*n и an до (n =12 включительно) ясно из табл. 2, в которой приведены все необходимые данные. При этом вначале по известным уже аn вычисляем an(2) =[anan] и
a*n+1, после чего, разделив найденное a*n+1 на его номер, определяем an+1
Проанализировав результаты, видим, что все нечетные коэффициенты
an=a2v+1= - 1; v=0,1,2,…
а все четные с ростом n стремятся к +1. Поэтому из решения (5.3) целесообразно вычесть ряд
/(1+ z)=1-z + z 2 - z3 + …
в результате чего получим
(5.5)
где коэффициенты bп определяются по формуле
bn=an - (- 1)n
и их значения приведены в последней колонке табл. 2
Так как
b2v+1=0; b2v=(- 1)v/2v+1; v=0,1,2,… то, просуммировав каждый из полученных рядов (5.5), находим решение уравнения (5.1) в замкнутом виде:
(5.6)
Подставив это значение в (5.1), после несложных преобразований убеждаемся, что оно удовлетворяет и самому дифференциальному уравнению, и начальному условию w(0)=3/2.
Таким образом, искомое решение имеет три полюса
z= - 1; z=€Ö2
благодаря чему радиус сходимости ряда (5.3) есть единица.
Формула (5.6), которую мы получили, исходя из ряда (5.3) полностью решает поставленную задачу. Однако просуммировать в явном виде полученный ряд удается лишь в простейших случаях, редко встречающихся на практике. Поэтому решим поставленную задачу, не прибегая к процессу суммирования ряда (5.3), а воспользовавшись его аналитическим продолжением и, кроме того, при помощи перехода к инверсной функции, что можно выполнить в случае любого получаемого ряда, суммируемого в явном виде или не суммируемого.
Ряд (5.3) является только элементом решения уравнения (5.1), определенным в круге с центром z0= 0 и проходящим через ближайшую к z0 особую точку z= - 1. Но этот элемент мы можем аналитически продолжить на полную область его определения, которой чаще всего является вся комплексная область, за исключением сколь угодно малых окрестностей изолированных особых точек. (Могут встретиться и такие случаи, когда окружность сходимости исходного элемента состоит из всюду плотного множества особых точек, так что исходный ряд за нее нельзя аналитически продолжить, но мы такие исключительные случаи рассматривать не будем.)
Для того чтобы аналитически продолжить исходный элемент (5.3), необходимо только вычислить для нового центра z0 значение функции w0=w(z0) и в случае необходимости перестроить рекуррентную формулу (5.4). В качестве нового центра z0 можно, вообще говоря, взять любую точку комплексной плоскости, лежащую внутри круга сходимости исходного ряда (5.3). Однако не любой выбранный центр z0 будет приводить к расширению круга сходимости исходного ряда, так что мы должны предварительно испытать ряд проб и найти такую последовательность центров z0(I), z0(II), z0(III), которая ведет к поставленной цели.
В качестве первой пробы возьмём z0=z0(1)=+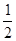 
Тогда, выполнив в уравнении (5.2) замену независимой переменной
z=t+z0(1)=t+ ;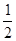
(5.7)
приходим к уравнению
2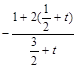 
, 
или после очевидных преобразований
, (5.8)
где
Следовательно, коэффициентыan=an* ряда I
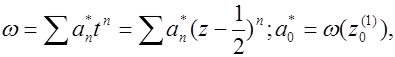
(5.9)
будут определяться рекуррентной формулой
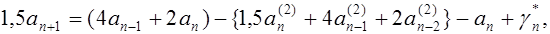(5.10)
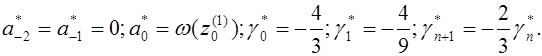
В табл. 3 по формулам (5.10) вычислены с семью десятичными знаками 17 коэффициентов аn= аn* ряда I. Значение a*0= 1,1111111…, без знания которого нельзя начать рекуррентный процесс (5.10), мы определили при помощи исходного ряда (5.3)
положив в нем z=z0(I)=1/2. При этом для обеспечения требуемой точности выполненное в табл. 2 вычисление коэффициентов аn надо продолжить до n = 24. Для контроля найденных коэффициентов an* ряда I определяем w(t) при t= - 0,5, т.е. при z=t + 0,5 =0, и в результате получаем
w(t)½ t=-0.5=w(z)½ z=0= 1,5000000,
что в пределах точности вычислений полностью совпадает с исходным начальным значением (5.1)
w(z)½ z=0=w(z0)=3/2
Вычислив с помощью ряда I по тем же коэффициентам an* значение w(t) при t= + 0,5, т.е. при
Z=t + 0,5 =1, получаем новое начальное значение
w(z)½ z=z0=1=w(z0(II))= 0,8333333,
определяющее собой ряд II с центром z0=z0(II)= + 1:
(5.11)
который является аналитическим продолжением ряда I (рис. 3). Рекуррентная формула для определения коэффициентов an =an** ряда II будет иметь следующий вид:
(5.12)
Действительно, произведя в (5.1) подстановку
(5.12)
Первые 16 коэффициентов an = an** ряда II вычислены в табл. 4, а для контроля этих вычислений умножим найденные аn** на tn для t= - 0.5, т.е. для z = t + 1 = 0.5, стоящие в тех же строках, и, просуммировав результаты, получаем
w(t)½ t=-0.5=w(z)½ z=0.5= 1,1111111,
Что полностью совпадает с начальным значением w(z0(I))=a0*=1,1111111 ряда I.
Вычислив аналогичным путем
w(t)½ t=0.5=w(z)½ z=1.5= 0,6352941.
мы можем использовать этот результат для построения ряда III. Однако сходимость ряда II значительно лучше сходимости ряда I, в чем легко убедиться, проанализировав быстроту убывания коэффициентов an* и an**, а также сравнив результаты, полученные в табл. 3 для t = 1 и t = 1 с соответствующими точными значениями. Поэтому мы можем с помощью ряда II вычислить (при п = 15 с пятью десятичными знаками) начальное значение
w(t)½ t=1=w(z)½ z=2 =0,50000,
соответствующее центру z0=z0(III) = + 2, и построить затем ряд III, сходящийся еще быстрее.
Продолжая этот процесс, мы будем получать ряды, сходящиеся все быстрее и быстрее, так что, определив по формуле (3.12) § 3 радиусы сходимости для двух из них, найдем затем полюсы z =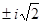 
, как точки пересечения окружностей сходимостей этих рядов. Но это процесс довольно трудоемкий, а потому более целесообразно перейти к инверсной функции.
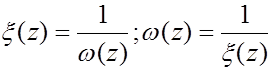( 5.14)
нули которой будут являться полюсами исследуемой функции w (и наоборот).
Переход к инверсной функции проще всего осуществить при помощи подстановки
(5.15)
Тогда из (5.1) получаем уравнение
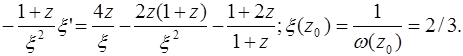
или, умножив обе части на (1 + z) x2 и поменяв знаки,
(5.16)
Решение этого уравнения ищем в виде ряда
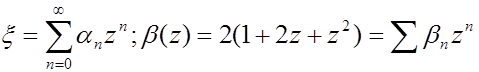(5.17)
и для коэффициентов an получаем рекуррентную формулу
(5.18)
a0=1/a0=2/3; b0=0; b1=2; b2=4; b3=2; bn=0 при n³4Нули функции x находим, определяя корни уравнения 
по формуле Ньютона
(5.19) При этом производную x(z) находим, пользуясь коэффициентами a*n которые были уже вычислены в процессе определения коэффициентов an по формуле (5.18).
В табл. 5 вычислены первые 24 коэффициента an по которым затем, исходя из нулевого приближения z0(0) =-0,8, после двух уточнений по формуле Ньютона находим один из нулей z2(0)= - 1,00001 инверсной функции x(z). Выполнив еще один шаг, получаем
z(0)=z3(0)= - 1,000000.
Следовательно, одним из полюсов исследуемой функции w=1/x(z) будет точка z= - 1,000000.
Выделив этот полюс из исходного ряда (5.3), аналогичным путем определяем два других полюса, на чем и заканчиваем решение поставленной задачи.
Коэффициенты an для инверсной функции можно также непосредственно найти по коэффициентам исходного ряда (5.3), так как, согласно (5.14), имеем
(5.20)
Тогда, представив единицу в следующем виде:
при n ³2
И воспользовавшись формулами:
получаем:
an= - a0(a0an+a1an-1+ … +an-1a1); a0=1/a0=2/3. (5.21)
где an - коэффициенты исходного ряда (5.3).
Приложение А
Исследование решений дифференциальных уравнений в окрестности полюсов и особых точек
Программа
ФОРМА - ЗАСТАВКАSub Command1_Click()SubSub Command2_Click(). Visible = False. Visible = TrueSubSub Ex_Click()SubSub Form_Load(). Visible = TrueSubSub prog_Click(). Visible = False. Visible = TrueSub
ФОРМА - ВВОД ЗНАЧЕНИЙSub Command1_Click()Text1 = «0» Or Text1 = «» Or Text2 = «» Or Text3 = «» Or Text4 = «» Or Text5 = «» Or Text6 = «» Then
Beep. Caption = «Введите все коэффициенты, первый не должен равняться 0»
ElseIf Text1 = «0» Or Text1 = «» Or Text2 = «» Or Text3 = «» Or Text4 = «» Or Text5 = «» Or Text6 = «» Then
Beep. Caption = «Введите все коэффициенты, первый не должен равняться 0»
Else= Text1= Text2= Text3= Text4= Text5= Text6= 0. Caption = «». Visible = False. Visible = TrueIfSub
ФОРМА - ИНФОРМАЦИЯnum As Integer
Dim num2 As Integernum1 As Integerds1 As Doubleds2 As DoubleSub Command1_Click(). Visible = False. Visible = TrueSubSub Command4_Click(). Visible = False. Visible = TrueSubSub Command5_Click(). Visible = False. Visible = TrueSubSub Form_Load(). Visible = True. Visible = Falsek1 = 0 Then k1 = 1. ColAlignment(0) = 3. ColAlignment(4) = 3. ColAlignment(1) = 3. ColAlignment(2) = 3. ColAlignment(3) = 3. ColWidth(0) = 500. ColWidth(4) = 1300. ColWidth(2) = 1300. ColWidth(3) = 1300. ColWidth(1) = 1300(-2) = 0(-1) = 0(0) = w0(0) = -1(-2) = 0(-1) = 0(0) = 0i% = 0 To 25i > 0 And i / 2 = Int (i / 2) Then ny(i) = 1 Else ny(i) = -1j% = 0 To i(i) = a2 (i) + a(j) * a (i - j)j(i + 1) = (k5 * a (i - 1) + (k4 * a2 (i - 1) + k3 * a2 (i - 2)) - k2 * at(i) + ny(i)) / k1(i + 1) = at (i + 1) / (i + 1)i / 2 = Int (i / 2) Then wan% = 1 Else wan = -1(i) = a(i) - wanii = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = a (i - 1). TextMatrix (i, 2) = a2 (i - 1). TextMatrix (i, 3) = at (i - 1). TextMatrix (i, 4) = ny (i - 1)iSubSub Command2_Click()SubSub HS1_Change()= HS1. Valuenum1 > num Theni = num + 1 To num1 + 1. TextMatrix (i, 0) = «». TextMatrix (i, 1) = «». TextMatrix (i, 2) = «». TextMatrix (i, 3) = «». TextMatrix (i, 4) = «»iIf. Caption = num. Caption = «Нажмите <обновить>»= numSubSub Command3_Click(). Caption = «»(0) = w0i% = 0 To 50i > 0 And i / 2 = Int (i / 2) Then ny(i) = 1 Else ny(i) = -1(i) = 0j% = 0 To i(i) = a2 (i) + a(j) * a (i - j)j(i + 1) = (k5 * a (i - 1) + (k4 * a2 (i - 1) + k3 * a2 (i - 2)) - k2 * at(i) + ny(i)) / k1(i + 1) = at (i + 1) / (i + 1)i / 2 = Int (i / 2) Then wan% = 1 Else wan = -1(i) = a(i) - wanii = 0 To 25j = 1 To 10= Format (a(i) / a (i + j), «0.000»)= Format (a(i + j) / a (i + 2 * j), «0.000»)ds1 < 0 Then ds1 = ds1 * (-1)ds2 < 0 Then ds2 = ds2 * (-1)ds1 = ds2 Then Label7. Caption = ds1ji= Label7. Captionnum2 = 0 Then num2 = 1Case num21i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.0»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.0»). TextMatrix (i, 3) = Format (at(i - 1), «0.0»). TextMatrix (i, 4) = ny (i - 1)i2i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.00»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.00»). TextMatrix (i, 3) = Format (at(i - 1), «0.00»). TextMatrix (i, 4) = ny (i - 1)i3i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.000»). TextMatrix (i, 3) = Format (at(i - 1), «0.000»). TextMatrix (i, 4) = ny (i - 1)i4i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.0000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.0000»). TextMatrix (i, 3) = Format (at(i - 1), «0.0000»). TextMatrix (i, 4) = ny (i - 1)i5i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.00000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.00000»). TextMatrix (i, 3) = Format (at(i - 1), «0.00000»). TextMatrix (i, 4) = ny (i - 1)i6i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.000000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.000000»). TextMatrix (i, 3) = Format (at(i - 1), «0.000000»). TextMatrix (i, 4) = ny (i - 1)i7i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.0000000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.0000000»). TextMatrix (i, 3) = Format (at(i - 1), «0.0000000»). TextMatrix (i, 4) = ny (i - 1)i8i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.00000000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.00000000»). TextMatrix (i, 3) = Format (at(i - 1), «0.00000000»). TextMatrix (i, 4) = ny (i - 1)i9i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.000000000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.000000000»). TextMatrix (i, 3) = Format (at(i - 1), «0.000000000»). TextMatrix (i, 4) = ny (i - 1)i10i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a(i - 1), «0.0000000000»). TextMatrix (i, 2) = Format (a2 (i - 1), «0.0000000000»). TextMatrix (i, 3) = Format (at(i - 1), «0.0000000000»). TextMatrix (i, 4) = ny (i - 1)iSelectSubSub HS2_Change()= HS2. Value. Caption = num2. Caption = «Нажмите <обновить>»Sub
ФОРМА - ИНФОРМАЦИЯ О ПРОГРАММЕ
Private Sub Command1_Click(). Visible = True. Visible = FalseSubSub Form_Load(). Caption = «Данный программный продукт составил студент КнАГТУ группы 6ПМ-1 Давыдов Андрей Анатольевич. Программа позволяет решить дифференциальное уравнение, а также исследовать полученные полюса и особенно существенные точки»
End Sub
ФОРМА - ВЫБОР МЕТОДАSub Command1_Click()Option1. Value = True Then. Visible = True. Visible = FalseOption1. Value = True Then. Visible = True. Visible = FalseIfOption2. Value = True And Text1 <> «» Then. Visible = True= Text1= «». Value = True= «»= «»= «». Label6. Caption = z1. Visible = FalseOption2. Value = True And Text1 = «» Then
Beep= «Необходимо ввести z1»
ElseIfSubSub Option1_Click()= «»= «»= «»= «»SubSub Option2_Click()= «Введите значение z1= (<z1<)»= z0 - radius1= z0 + radius1Sub
ФОРМА - ИССЛЕДОВАНИЕ ПОЛЮСОВ
Dim num As Integer
Dim num2 As Integernum15 As Integersum As Doubleds1 As Doubleds2 As Doubleds3 As DoubleSub Command3_Click()SubSub Command4_Click()Text1 = «» Then= «Необходимо ввести радиус»Text1 = «» Then
Beep= «Необходимо ввести радиус»
Else= Text1= «». Label3 = z1 - radius2. Label4 = z1 + radius2. Visible = False. Visible = TrueIfSubSub Command5_Click(). Visible = False. Visible = TrueSubSub Form_Load(). ColAlignment(0) = 3. ColAlignment(4) = 3. ColAlignment(1) = 3. ColAlignment(2) = 3. ColAlignment(3) = 3. ColWidth(0) = 300. ColWidth(4) = 1600. ColWidth(2) = 1300. ColWidth(3) = 1300. ColWidth(1) = 1300i% = 0 To 24n(i) = 1j% = 0 To ij = 0 Then z1n(i) = 1 Else z1n(i) = z1n(i) * z1j= sum + z1n(i) * a(i)i(-2) = 0(-1) = 0(0) = sum(0) = -2 + 1 / (1 + z1)(1) = - (1 / ((1 + z1) * (1 + z1)))(-2) = 0(-1) = 0(0) = 0i = 0 To 25i > 1 Then ny1 (i) = 0i > 1 Then ny1 (i) = - (1 / (1 + z1)) * ny1 (i - 1)(i) = 0j = 0 To i(i) = a21 (i) + a1 (j) * a1 (i - j)j(i + 1) = (k5 * a1 (i - 1) + k5 * z1 * a1 (i) + k3 * a21 (i - 2) + (2 * k3 * z1 + k4) * a21 (i - 1) + (k4 * z1 + k3 * z1 * z1) * a21 (i) - k1 * at1 (i) + ny1 (i)) / (k1 + k1 * z1)(i + 1) = at1 (i + 1) / (i + 1)n(i) = 1ii = 1 To num15 + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0»)iSubSub Command1_Click(). Visible = False. Visible = TrueSubSub HS1_Change()= HS1. Valuenum15 > num Theni = num + 1 To num15 + 1. TextMatrix (i, 0) = «». TextMatrix (i, 1) = «». TextMatrix (i, 2) = «». TextMatrix (i, 3) = «». TextMatrix (i, 4) = «»iIf. Caption = num. Caption = «Нажмите <обновить>»= numSubSub Command2_Click(). Caption = «»= 0i% = 0 To 24n(i) = 1j% = 0 To ij = 0 Then z1n(i) = 1 Else z1n(i) = z1n(i) * z1j= sum + z1n(i) * a(i)i(0) = sum(0) = -2 + 1 / (1 + z1)(1) = - (1 / ((1 + z1) * (1 + z1)))i% = 0 To 50i > 1 Then ny1 (i) = 0i > 1 Then ny1 (i) = - (1 / (1 + z1)) * ny1 (i - 1)(i) = 0j% = 0 To i(i) = a21 (i) + a1 (j) * a1 (i - j)j(i + 1) = (k5 * a1 (i - 1) + k5 * z1 * a1 (i) + k3 * a21 (i - 2) + (2 * k3 * z1 + k4) * a21 (i - 1) + (k4 * z1 + k3 * z1 * z1) * a21 (i) - k1 * at1 (i) + ny1 (i)) / (k1 + k1 * z1)(i + 1) = at1 (i + 1) / (i + 1)n(i) = 1j = 0 To ij = 0 Then z1n(i) = 1 Else z1n(i) = z1n(i) * z1ji. Caption = z1num2 = 0 Then num2 = 1Case num21i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0»)i2i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.00»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.00»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.00»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.00»)i3i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.000»)i4i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0000»)i5i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.00000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.00000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.00000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.00000»)i6i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.000000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.000000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.000000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.000000»)i7i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0000000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0000000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0000000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0000000»)i8i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.00000000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.00000000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.00000000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.00000000»)i9i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.000000000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.000000000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.000000000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.000000000»)i10i = 1 To num + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0000000000»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0000000000»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0000000000»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0000000000»)iSelectSubSub HS2_Change()= HS2. Value. Caption = num2. Caption = «Нажмите <обновить>»Sub
ФОРМА - ВВОД ЗНАЧЕНИЯ z1Sub Command1_Click()Text1 = «» Then
Label2. Caption = «Необходимо ввести значение z2»
ElseIf Text1 = «» Then. Caption = «Необходимо ввести значение z2»
Else= Text1= «». Label6 = z1. Label7 = z2. Visible = False. Visible = TrueIf Sub
ФОРМА - ИССЛЕДОВАНИЕ ПОЛЮСОВ 2
Dim num As Integer
Dim num2 As Integernum15 As Integersum As Doubleds1 As Doubleds2 As Doubleds3 As DoubleSub Command1_Click(). Visible = False. Visible = TrueSubSub Command3_Click()SubSub Command4_Click()
If Text1 = «» Then= «Необходимо ввести радиус»Text1 = «» Then= «Необходимо ввести радиус»
Beep= Text1= «»= (radius2 * radius2 - radius1 * radius1 - z1 * z1) / (-2 * z1)(radius1 * radius1 - x1 * x1) < 0 Then
Label10 = «Введеные радиусы не корректны»
ElseIf (radius1 * radius1 - x1 * x1) >= 0 Then= Sqr (radius1 * radius1 - x1 * x1)= (radius3 * radius3 - radius2 * radius2 - z2 * z2 + z1 * z1) / (2 * (z1 - z2))(radius2 * radius2 - (x2 + z1) * (x2 + z1)) < 0 Then
Label10 = «Введеные радиусы не корректны»
ElseIf (radius2 * radius2 - (x2 + z1) * (x2 + z1)) >= 0 Then= Sqr (radius2 * radius2 - (x2 + z1) * (x2 + z1))y2 < 0 Then. Label3 = «z2= i». Label4 = «z3= + i»y2 < 0 Then. Label3 = «z2= i». Label4 = «z3= + i». Label4 = «z3= i». Label3 = «z2= + i»If. Visible = False. Visible = True. Label6 = Format (x1, «0.000»). Label7 = Format (y1, «0.000»). Label8 = Format (x2, «0.000»). Label9 = Format (y2, «0.000»). Label10 = Format (x2, «0.000»). Label11 = Format (-1 * y2, «0.000»)IfIfIfSubSub Command5_Click(). Visible = False. Visible = TrueSubSub Form_Load(). ColAlignment(0) = 3. ColAlignment(4) = 3. ColAlignment(1) = 3. ColAlignment(2) = 3. ColAlignment(3) = 3. ColWidth(0) = 300. ColWidth(4) = 1600. ColWidth(2) = 1300. ColWidth(3) = 1300. ColWidth(1) = 1300. ColAlignment(0) = 3. ColAlignment(4) = 3. ColAlignment(1) = 3. ColAlignment(2) = 3. ColAlignment(3) = 3. ColWidth(0) = 300. ColWidth(4) = 1600. ColWidth(2) = 1300. ColWidth(3) = 1300. ColWidth(1) = 1300= Form9. Text1i% = 0 To 24n(i) = 1j% = 0 To ij = 0 Then z2n(i) = 1 Else z2n(i) = z2n(i) * (z2 - z1)j= sum + z2n(i) * a1 (i)i(-2) = 0(-1) = 0(0) = sum(0) = -2 + 1 / (1 + z2)(1) = - (1 / ((1 + z2) * (1 + z2)))(-2) = 0(-1) = 0(0) = 0i = 0 To 25i > 1 Then ny2 (i) = - (1 / (1 + z2)) * ny2 (i - 1)(i) = 0j = 0 To i(i) = a22 (i) + a12 (j) * a12 (i - j)j(i + 1) = (k5 * a12 (i - 1) + k5 * z2 * a12 (i) + k3 * a22 (i - 2) + (2 * k3 * z2 + k4) * a22 (i - 1) + (k4 * z2 + k3 * z2 * z2) * a22 (i) - k1 * at2 (i) + ny2 (i)) / (k1 + k1 * z2)(i + 1) = at2 (i + 1) / (i + 1)n(i) = 1ii = 1 To num15 + 1. TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a1 (i - 1), «0.0»). TextMatrix (i, 2) = Format (a21 (i - 1), «0.0»). TextMatrix (i, 3) = Format (at1 (i - 1), «0.0»). TextMatrix (i, 4) = Format (ny1 (i - 1), «0.0»). TextMatrix (i, 0) = i - 1. TextMatrix (i, 1) = Format (a12 (i - 1), «0.0»). TextMatrix (i, 2) = Format (a22 (i - 1), «0.0»). TextMatrix (i, 3) = Format (at2 (i - 1), «0.0»). TextMatrix (i, 4) = Format (ny2 (i - 1), «0.0»)iSubSub HS1_Change()= HS1. Valuenum15 > num Theni = num + 1 To num15 + 1. TextMatrix (i, 0) = «». TextMatrix (i, 1) = «». TextMatrix (i, 2) = «». TextMatrix (i, 3) = «». TextMatrix (i, 4) = «». TextMatrix (i, 0) = «». TextMatrix (i, 1) = «». TextMatrix (i, 2) = «». TextMatrix (i, 3) = «». TextMatrix (i, 4) = «» If
Заключение
В результате выполнения дипломной работы были решены дифференциальные уравнения и исследованы полученные решения в окрестности полюсов двумя способами. Разработана методика исследования решений в комплексной области и представления результата в виде действительной и мнимой частей без относительной затраты времени и огромного объема вычислений. Приблизительно, производительность программы по скорости вычислений превышает в десятки тысяч раз. Программа выдает желаемое количество полученных коэффициентов (от 1 до 25) с желаемой точностью (от 1 до 10 знаков после запятой). В результате значительной доработки данной дипломной работы можно устранить необходимость ввода радиусов сходимости полученных рядов, но по предварительным расчетам необходимо будет вычислять до 300 коэффициентов исследуемого ряда, что в некоторых случаях будет приводить к переполнению переменных в коде программы.
Список источников
1. Кудрявцев Л.Д. «Курс математического анализа» Т.1, М., ВШ., 1981 г. - 687 с.
2. Фильчаков П.Ф.» Численные и графические методы прикладной математики» Справочник, К., «Наукова думка», 1970 г. - 798 с.
3. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. - 13-е изд., исправленное. - М.,:Наука, 1986 - 544 с.
4. Михаэль Райтингер, Геральд Муч. Visual Basic 6: полное руководство: пер. с нем. - К.: Издательская группа BHV, 2000. - 720 с.
5. Данилина Н.И., Дубровская Н.С. Численные методы. - М.: «Высшая школа», 1976 - 368 с.
6. Мышкис А.Д. Математика для ВТУЗов. Спец. Курсы. - М.:» Наука». 1971 - 632 с.
7. Данко П.Е., Попов А.Г. Теория функций комплексного переменного. - М.: «Высшая школа». 1986 - 415 с.
8. Фролов С.Н., Шостак Р.Я. Численные методы. - М.: «Высшая школа». 1972 - 472 с.