Рассмотрим задачу Коши для уравнения n-го порядка, разрешенного относительно старшей производной
(n)=(х, у, у’,…, y(n -1)); (3.1)
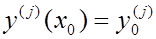; j = 0, 1, 2,…, n - 1. (3.2)
Будем искать формальное решение задачи (3.1) - (3.2) в виде степенного ряда
, (3.3)
так что в каждом конкретном случае необходимо дополнительно исследовать, может ли данная задача Коши быть решена при помощи ряда (3.3).
Обозначим k-ю степень ряда (3.3) соответственно
, k = 1, 2, 3,… (3.4)
и выведем рекуррентную формулу для вычисления введенных коэффициентов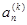 
Так как для произвольного k=l+m имеет место тождество,
,
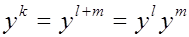то воспользовавшись формулой Коши для умножения степенных рядов
аn=b0 cn +b1cn-1+b2 cn-2+ … +bn-1 c1+bn c0.
непосредственно получаем искомую рекуррентную формулу:
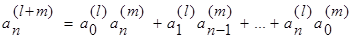(3.5)
где l= 1, 2, 3,…; m= 1, 2, 3,…; n = 0, 1, 2, 3, …
В частности, при k = 1 ряд (1.4) тождественно совпадает с рядом (3.3), так что
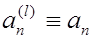; п =0.1, 2,…, (3.6)
и тогда при помощи формулы (3.5) легко определить коэффициенты а(k)n для произвольной целой степени ряда yk через коэффициенты исходного ряда (3.3).
Для удобства выкладок представим производные у’, у»,… в виде таких рядов
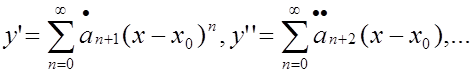(3.7)
где введены обозначения
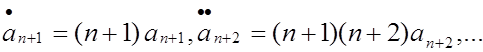(3.8)
В таком случае и все степени от производных у', у»,… легко выразить рядами
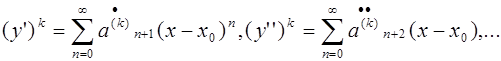(3.9)
коэффициенты которых
определим при помощи формулы (3.5), если в этой формуле an заменим соответственно на
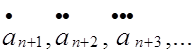
Если мы теперь подставим ряды (3.3), (3.4), (3.7), (3.9) в исходное уравнение (1.1) и приравняем коэффициенты при одинаковых степенях (x - x0) то после соответствующих упрощений, получим рекуррентную формулу вида:
(3.10)
где функция F полностью определяется заданной функцией ¦(х, у, у',…, y(v-1)), а первые v коэффициентов, согласно начальным условиям (3.2), будут такими:
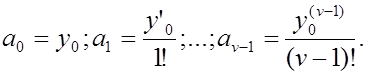(3.11)
В том случае, когда существует предел 
радиус сходимости ряда (3.3) можно определить численно, если вычислить достаточное количество членов последовательности
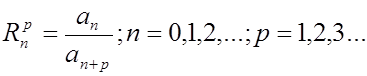(3.12)
до такого значения n включительно, начиная с которого будет иметь место равенство
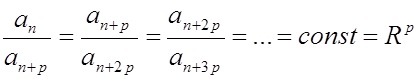(3.13)
с необходимой для данной задачи точностью.
В отдельных частных случаях радиус сходимости ряда (3.3) можно найти, исходя из самой рекуррентной формулы (3.10).
Рассматриваемый метод позволяет также построить аналитическое продолжение ряда (3.3) и выявить особые точки найденного решения. Для этого в любой точке х1, где [x1-x0] < R, вычисляем при помощи ряда (3.3) новые начальные значения
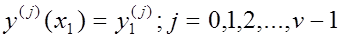(3.14)
и, подставив их в ту же самую рекуррентную формулу (3.10), находим коэффициенты а*n нового ряда
который, согласно известной теореме об аналитическом продолжении решений дифференциального уравнения, и есть аналитическое продолжение ряда (3.13).
Особые точки решения находим как точки пересечения двух или трех окружностей сходимости соответствующих аналитических продолжений. Если найденная особая точка есть полюс, то его легко выделить, перестроив соответствующим образом ряд (3.13).
Все полученные результаты имеют место также и в комплексной области.
Для пояснения методики вычислений рассмотрим пример.
Пример. Решим с семью десятичными знаками на сегменте [-1; +1] задачу Коши для нелинейного уравнения третьего порядка:
y’’’=2y’+y3-¦(x); ¦(х)=sh(x) (1/x). (3.16)
при следующих начальных условиях:
x0=0; y(0)=1; y’ (0)=1; y’’ (0)=1/2. (3.17)
Решение. Подставив в исходное уравнение (3.16) ряды (3.13), (3.14), (3.17) при x0 = 0, k = 3, в результате сравнения коэффициентов при хn имеем:
(3.18)
bn есть коэффициенты ряда Маклорена для заданной функции
в данном случае
Заменив теперь по формуле (3.8)
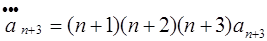
и учтя, что согласно начальным условиям (3.17)
a0=1; a1=1; a2=1/4,
находим из (3.18) рекуррентную формулу (3.10) для уравнения (3.16);
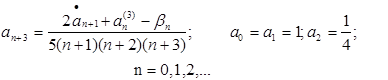(3.19)
Коэффициенты a*n вычисляем по формуле (1.8), а коэффициенты аn(3) - по формуле (1.5), в которой надо вначале положить l=m= 1, а затем l= 1, т = 2, в результате чего получим
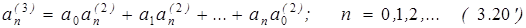
Все вычисления (с одним запасным знаком) приведены в табл. 1, и окончательным решением будет ряд
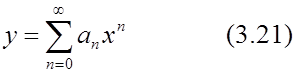
Согласно (3.13), радиус сходимости полученного ряда
так что при п = 15 заданная точность для |x|£1 будет выполнена.
Методика вычислений по формулам (3.20) - (3.20') очень проста.
По известным а0, а1, а2 вычисляем а*1=а1 и а*2=а2, а также а0(2), а1(2), а2(2), после чего, перемножив столбец аn на столбец аn(2), находим соответствующий коэффициент аn(3).В результате получаем все необходимые данные для вычисления по рекуррентной формуле (1.19) а3 и а4, что позволяет продолжить дальше этот процесс и определить любое количество коэффициентов аn искомого ряда (3.21).
Для удобства ориентировки каждый из сомножителей, который используется в данный момент, отмечаем какими-либо марками. Столбец аn(2) вычисляем, умножив столбец аn сам на себя. Например,n(2) = 1.00000000 * 0,25000000 + (1.00000000)2 + 0,25000000 *1,00000000 = 1,50000000.
an(3) = 1,00000000 * 1,50000000 + 1,00000000 * 2,00000000 + 0,25000000 * 1,00000000 = =3,75000000.
Ход дальнейших вычислений ясен из табл. 1, в которой все величины, необходимые для определения очередного аn+3, размещены в одной строке.
Для того чтобы точнее определить радиус сходимости R, вычисления надо вести с большим числом значащих цифр, и если мы это выполним, то получим, например,
a12=5,7341*10-6; a13=1,8765*10-6;… по которым в табл. 1 найдены соответствующие аn/an+1
Уравнение Риккати
Уравнение Риккати (1676-1754) - одно из простейших нелинейных дифференциальных уравнений первого порядка.