Введение
При решении дифференциальных уравнений степенными рядами каждый полученный ряд является только элементом искомого решения, определенным в его области сходимости. Область сходимости степенного ряда есть круг, на границе которого должна находиться по крайней мере одна особая точка решения исходного дифференциального уравнения. Поэтому для того, чтобы распространить полученные результаты на всю комплексную область, прежде всего надо провести исследования поведения решений в окрестности полюса и существенно особой точки, которые на практике встречаются наиболее часто. Однако, этот процесс при реализации его в ручную довольно трудоемкий. В связи с этим появляется возможность запрограммировать данную задачу и сравнить полученный результат с уже проведенными вычислениями. Попытка именно этого и предпринята в данной дипломной работе.
Вводные замечания
Степенные ряды. Радиус сходимости
Наиболее простыми будут ряды, сходящиеся не только абсолютно, но и равномерно. К таким рядам относятся и степенные, чем и обусловлено то особо важное значение, которое они имеют в самых различных областях математики и ее приложениях.
Определение. Степенным рядом (точнее, целым степенным) называется бесконечный ряд вида
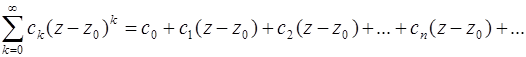 (1.1)
(1.1)
где сk и z0 - заданные комплексные числа, не зависящие от z. Число z0 для краткости называют центром ряда. В частности, может быть z0 = 0.
Выясним прежде всего область сходимости степенного ряда, для чего докажем следующую теорему.
Первая теорема Абеля (1826).
Если степеннойряд

сходится в некоторой точке z=z1, то он сходится, и притом абсолютно и равномерно, во всяком круге с центром z0 и радиусом r< | z - z0|, т.е. радиусом, меньшим, чемрасстояние от z1 до z0 (рис. 1).
Переходя к доказательству теоремы, предположим, что z - произвольная точка круга |z - z0| < р < | z1 - z0|, и представим n-й член ряда (1.1) в виде

Из сходимости ряда в точке z1, которая имеет место по условию теоремы, вытекает, что
| cn(z1 - z0)n | £ M
для всех n, где М - некоторое положительное число. Кроме того, в силу нашего предположения
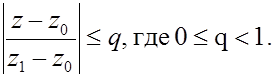
Следовательно, для всех n

откуда и вытекает по признаку Вейерштрасса абсолютная и равномерная сходимость ряда внутри круга | z - z0 | £ р < | z1 - z0 |, так как члены рассматриваемого ряда по модулю меньше членов убывающей геометрической прогрессии, составленной из положительных чисел.
В частности, ряд сходится абсолютно (но, вообще говоря, не равномерно) во всех точках круга | z - z0 | < | z1 - z0 |. Отсюда вытекает, что если степенной ряд расходится при некотором значений z = z1 то он расходится и при всяком значении z, для которого
| z - z0 | > | z1 - z0 |,
Теорема, сформулированная выдающимся норвежским математиком Нильсом Генриком Абелем (1802-1829), играет в теории степенных рядов исключительно важную роль, и, в частности, из этой теоремы следует, что степенной ряд сходится в некотором круге, радиус которого будем обозначать через R, причем ряд сходится
абсолютно при
| z - z0 | < R,
расходится при
| z - z0 | > R,
и равномерно сходится в любом круге
| z - z0 | £ р < R
На самом же круге | z - z0 | = R ряд может быть сходящимся или расходящимся, и установление этого факта требует дополнительных исследований, иногда очень сложных.
Радиус этого круга R называется радиусом сходимости степенного ряда, а сам круг - кругом его сходимости. Для определения радиуса сходимости R служит формула
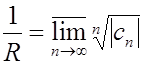 (1.2)
(1.2)
где lim обозначает верхний предел.
Эта формула была получена Огюстом Луи Коши в 1821 г. и со всей строгостью доказана в 1893 г. Жаком Адамаром (1865-1963). Она называется формулой Коши - Адамара.
Радиус сходимости можно также определять по формуле, вытекающейиз признака сходимости рядов Даламбера;
 (1.3)
(1.3)
если только указанный предел существует.
В частности, R может равняться нулю (тогда сумма ряда сводится к его первому члену c0) или бесконечности (тогда ряд сходится во всей комплексной плоскости z).
На основании теорем о сумме ряда и доказанной равномерной сходимости степенного ряда внутри его круга сходимости вытекают весьма важные свойства степенных рядов, которые мы сформулируем в виде следующих теорем.
Теорема 1. Сумма степенного ряда есть непрерывная функция от z внутри круга сходимости ряда.
Этот результат дополняется второй теоремой Абеля (1826): если степенной ряд сходится в точке z окружности | z - z0 | = R, то его сумма s(z) есть функция, непрерывная в точке z1 самой окружности вдоль радиуса, идущего из центра z0 в точку z1.
А. Прингсхейм доказал, что при условиях этой теоремы s(z) непрерывна в точке z1 вдоль любой линии, которая не касается окружности в точке z1.
Теорема 2. Степенной ряд внутри круга его сходимости можно почленно интегрировать, и сумма полученного ряда будет представлять собой интеграл от суммы данного ряда:
 (1.4)
(1.4)
Теорема 3. Степенной ряд внутри круга его сходимости можно почленно дифференцировать, и его сумма будет представлять собой производную от суммы данного степенного ряда:
 (1.5)
(1.5)
Для того чтобы последнее свойство имело место, надо еще доказать, что ряд, полученный по членным дифференцированием, имеет тот же радиус сходимости R (в силу чего он также будет равномерно сходящимся рядом).
Пусть z - некоторая точка внутри круга сходимости и R - число, удовлетворяющее неравенству | z - z0 | < R1 < R. Так как ряд

сходится абсолютно, то существует такое положительное число М, что

при всех значениях n.
Тогда для модуля общего члена ряда, полученного дифференцированием, имеем:

т.е. модули членов ряда (1.5) меньше соответствующих членов сходящегося по признаку Даламбера ряда. Следовательно, ряд (1.5) сходится абсолютно во всех точках внутри круга сходимости исходного степенного ряда

Если | z - z0 | > R, то cn(z - z0)n, а благодаря этому и ncn(z - z0)n-1 не стремится к нулю и ряд расходится.
Таким образом, ряд (1.5) и ряд

имеют один и тот же круг сходимости.
Следствие 2. Ряд
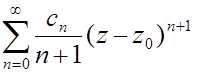 ,
,
полученный почленным интегрированием степенного ряда

имеет тот же радиус сходимости R, что и исходный ряд.
Действительно, если бы это было не так, то, дифференцируя почленно ряд
 ,
,
мы бы получили исходный ряд

с радиусом сходимости R1 ¹ R, что противоречит теореме 3.
Следует, однако, отметить, что из факта равенства радиусов сходимости данного степенного ряда и рядов, полученных почленным дифференцированием или интегрированием, нельзя сделать никаких выводов относительно характера сходимости этих рядов и на самой границе области сходимости, т.е. на самой окружности | z - z0 | = R.
Так, например, ряд

расходится во всех точках границы | z | = 1, тогда как после интегрирования получается ряд

сходящийся при z = - 1. Действительно, при z = - 1 имеем:

Аналогично ряд

радиус сходимости которого R= 1, абсолютно сходится во всех точках границы области сходимости | z | = 1, так как при | z |= 1

а ряд справа, как известно, сходящийся.
Продифференцировав же этот ряд, получим ряд

который на окружности | z | = 1 является расходящимся, по крайней мере в точке z = 1, как гармонический ряд
+ 1 / 2 + 1 / 3 + 1 / 4 + …
Приведенные примеры также хорошо иллюстрируют сказанное ранее о поведении ряда на самой границе области сходимости. А именно, на контуре сходимости ряд может быть всюду сходящимся (но отнюдь не обязательно абсолютно или равномерно сходящимся) или всюду расходящимся, или может сходиться только в отдельных точках и расходиться в других точках.
Следствие 2. Степенной ряд

в круге его сходимости | z - z0 | < R можно дифференцировать (и интегрировать) произвольное число раз. В результате получим новые степенные ряды, которые будут иметь тот же самый радиус сходимости R, суммы которых будут равны последовательным производным (или интегралам от) суммы ряда s (z).