Введение
Случай, случайность - с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находка, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики-какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности - они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hazard, буквально означающего «случай», «риск». Азартными называют те игры, а которых выигрыш зависит главным образом не от умения игрока, а от случайности. Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных-алгебраиста Джироламо Кардана (1501- 1576) и Галилео Галилея (1564-1642). Однако честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым - Блезу Паскалю (1623-1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность.
Определение и типы событий
Основополагающими понятиями в теории вероятностей являются понятие события и эксперимента.
Событие - это всякий факт, который может произойти или не произойти в результате эксперимента.
Эксперимент в теории вероятностей представляет собой идеализированную модель реально производимых экспериментов, результаты которых невозможно заранее предсказать. Несмотря на это случайное событие подчиняется довольно строго математике. Результат большого числа случайных событий перестает быть случайным и может быть предсказан с высокой точностью. В этом смысле, предметом теории вероятностей является изучение вероятных закономерностей большого числа однородных случайных явлений.
Наблюдаемые события можно разделить на три вида: достоверные, невозможные и случайные.
Вероятность - есть мера случайности события, мера возможности событию произойти или не произойти.
Событие называется достоверным, если оно обязательно произойдет в результате эксперимента.
Событие называется невозможным, если оно обязательно не произойдет в результате эксперимента.
Событие называется случайным, если при осуществлении ряда условий оно может либо произойти, либо не произойти.
Совместные события - события, при появлении одного из которых не исключается появление другого события. Несовместные события - события, при появлении одного из которых исключается появление другого.
События называются единственно возможными, если появление в результате эксперимента одного и только одного из них является достоверным событием.
Очевидно, единственно возможные события являются попарно несовместными.
События называются равновозможными, если можно считать, что ни одно из них не является более возможным, чем другие.
Элементарным исходом называется каждый из возможных результатов эксперимента.
Независимые события - события, наступление одного из которых не влияет на возможность наступления другого.
Зависимые события - события, наступление одного из которых влияет на возможность наступления другого.
Полной группой называется совокупность единственно возможных событий испытания.
Сумма вероятностей всех событий в группе всегда равна 1.
При рассмотрении экспериментов не учитываются маловероятностные исходы. События из полной группы должны быть равновозможными, т.е. нет предпосылок считать, что одно из них наступит скорее другого. Элементарные события обозначим 
, полная группа событий 
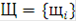. Тогда любое событие A может быть представлено подмножеством множества 
.
Противоположными называются два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через 
, то другое обозначают 
.
Примеры. 1. Выпадения орла или решки при подбрасывании монеты являются противоположными событиями. 2. Попадание и промах при стрельбе по мишени - противоположные события.
Рассмотрим несколько примеров событий. 1. Опыт - бросание монеты; событие A - появление герба. 2. Опыт - бросание трех монет; событие B - появление трех гербов. 3. Опыт - передача группы из n сигналов; событие C - искажение хотя бы одного из них. 4. Опыт - выстрел по мишени; событие D - попадание. 5. Опыт - вынимание наугад одной карты из колоды; событие Е - появление туза. 6. Тот же опыт, что в примере 5; событие F - появление карты червонной масти.
Рассматривая перечисленные в наших примерах события A,B,C, видим, что каждое из них обладает какой-то степенью возможности - одни большей, а другие меньшей, причем для некоторых из них мы сразу можем решить, какое из них более, а какое менее возможно. Например событие A более возможно (вероятно), чем B, а событие F более возможно, чем Е.
Пример. Для каждого из событий определить, каким оно является - невозможным, достоверным или случайным:
а) из списка 9 класса выбрали одного ученика и это - мальчик;
б) из списка 9 класса выбрали одного ученика и это - девочка;
в) из списка 9 класса выбрали одного ученика и ему - 14 месяцев;
г) из списка 9 класса выбрали одного ученика и ему больше двух лет;
д) измерили стороны треугольника и сумма двух из них оказалась меньше длины третьей стороны.
Решение.
Случайные - а, б
Достоверные - г
Невозможные - в, д
Пример. Для каждого из описанных событий определите, каким оно является: невозможным, достоверным или случайным.
Из 25 учащихся класса двое справляют день рождения: 1) 30 января; 2) 30 февраля.
Решение:
Событие, заключающееся в том, что двое из 25 учащихся родились 30 января - случайное, оно может произойти, а может и не произойти (все зависит от состава группы из 25 учащихся).
Второе событие - невозможное, поскольку даты 30 февраля не существует, следовательно, никто из учащихся не мог родиться в такой день
Пример. Назовите событие, противоположное данному:
) при бросании монеты выпала решка;
) Алеша вытащил выигрышный билет в розыгрыше лотереи;
) в нашем классе все умные и красивые;
) мою соседку по парте зовут или Таня, или Аня;
) явка на выборы была от 40% до 47%;
6) сегодня хорошая погода.
Решение.
) при бросании монеты выпал орёл;
) Алеша вытащил невыигрышный билет в розыгрыше лотереи;
) в нашем классе все глупые и некрасивые;
) мою соседку по парте зовут не Таня и не Аня;
) явка на выборы была менее 40% или более 47%
) сегодня плохая погода
Пример. В мешке лежат 10 шаров: 3 синих, 3 белых и 4 красных. Охарактеризуйте следующее событие как достоверное, невозможное или случайное;
) из мешка вынули 4 шара, и все они синие;
) из мешка вынули 4 шара, и все они красные;
) из мешка вынули 4 шара, и все они оказались разного цвета;
) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.
Решение:
) Событие невозможное, так как в мешке только 3 синих шара; четыре вынуть нельзя.
) Событие случайное, может произойти, может и не произойти.
) Событие невозможное, так как в мешке лежат шары только трех разных цветов.
) Событие достоверное, так как в мешке нет шаров черного цвета.
Пример. Событие В - в результате стрельбы по мишени хотя бы одна пуля попала в цель. Что означает событие 
?
Решение:
Событие можно описать так: "в результате стрельбы по мишени ни одна пуля не попала в цель". Оно означает, что все пули попали мимо цели.
Ответ: противоположное событие.
Пример. Из событий: 1) «идёт дождь»; 2) «на небе нет ни облака»; 3) «наступило лето» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
Решение: «идёт дождь» - «на небе нет ни облачка» - несовместные;
«наступило лето» - «на небе нет ни облачка» и «наступило лето» - «идёт дождь» - совместные.
Пример. Из событий: 1) «наступило утро»; 2) «сегодня по расписанию 6 уроков»; 3) «сегодня 1 января»; 4) «температура воздуха в Мариинске +30С» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
Решение: «сегодня 1 января» - «температура воздуха в Мариинске +30С»; «сегодня по расписанию 6 уроков» - «температура воздуха в Мариинске +30С»; «сегодня 1 января» - «сегодня по расписанию 6 уроков» - несовместные; «наступило утро»- «сегодня 1 января»; «наступило утро» - «температура воздуха в Мариинске +30С»; «наступило утро» - «сегодня по расписанию 6 уроков» - совместные.
Пример. Укажите события, противоположные данным: а) на кубике выпало 1; б) Света получила на экзамене «5»; в) после ночи наступает утро?
Решение. a) На кубике выпало от 2 до 6;
б) Света сдала экзамен не на “отлично”;
в) После утра наступает ночь?
Пример. Из полной колоды карт вынимается одна карта. Выяснить, являются совместными или несовместными события:
) «вынута карта красной масти» и «вынут валет»;
) «вынут король» и «вынут туз».
Решение. 1) Совместны, т.к. может быть вытянут валет красной масти;
) Несовместны, т.к. вытянута только одна карта.
Любое случайное событие обладает какой-то степенью возможности, которую в принципе можно измерить численно. Чтобы сравнивать события по степени их возможности, нужно связать с каждым из них какое-то число, которое тем больше, чем больше возможность события. Это число мы и назовем вероятностью события.
Вероятностью события А называется отношение числа благоприятных исходов к общему числу всех элементарных исходов испытания, если все исходы равновозможны (классическое определение вероятности). Формулой
это определяется так:
,
где m - число элементарных исходов, благоприятных событию A; n - число всех возможных элементарных исходов.
Из определения вероятности вытекают следующие свойства:
а) вероятность достоверного события равна единице;
б) вероятность невозможного события равна нулю;
в) вероятность случайного события есть положительное число, заключенное между нулем и единицей;
г) вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Очень большую роль в применении вероятностных методов играют практически достоверные и практически невозможные события.
Событие A называется практически невозможным, если его вероятность не в точности равна нулю, но очень близка к нулю: 
Пример: 32 буквы разрезной азбуки смешали между собой; наугад вынимается одна карточка, стоящая на ней буква записывается, карточка возвращается обратно и смешивается с другими. Такой опыт производится 25 раз. Событие A состоит в том, что после 25 выниманий мы запишем первую строчку "Евгения Онегина": "Мой дядя самых честных правил".
Событие A не является физически невозможным, но вероятность его настолько мала, что событие с такой вероятностью можно смело считать практически невозможным.
Аналогично, практически достоверным является событие, вероятность которого не в точности равна единице, но очень близка к единице: 
.
Пример: В ящике 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 10?
Решение. Так как номер любого шара, находящегося в ящике, не превышает 10, то число случаев, благоприятствующих событию А, равно числу всех возможных случаев, т.е. m = n = 10 и Р(A) = 1. В этом случае событие А достоверно.
Пример: В урне 15 шаров: 5 белых и 10 чёрных. Какова вероятность вынуть из урны синий шар?
Решение. Синих шаров в урне нет, т.е. m = 0, а n = 15. Следовательно,
Р(A) = 0/15 = 0. В данном случае событие А - невозможное.
Пример. В урне 12 шаров: 3 белых, 4 чёрных и 5 красных. Какова вероятность
вынуть из урны чёрный шар?
Решение. Здесь m = 4, n = 12 и Р(A) = 4/12 = 1/3.
Пример. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
Решение. а) Извлеченная стандартная деталь, очевидно, не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21 + 10-1=30), причем среди них было 20 стандартных (21-1=20). Вероятность того, что была потеряна стандартная деталь, Р = 20/30 = 2/3.
б) Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь, Р = 10/30= 1/3.
Непосредственный подсчёт случаев, благоприятствующих данному событию, может оказаться затруднительным. Поэтому для определения вероятности события бывает выгодно представить данное событие в виде комбинации некоторых других, более простых событий. Приведём теоремы, с помощью которых можно по вероятностям одних случайных событий вычислять вероятности других случайных событий, каким - либо образом связанных с первыми.
Теорема 1. Пусть А и В - два несовместных события. Тогда вероятность того, что осуществится хотя бы одно из этих двух событий, равна сумме их вероятностей:
Пример. Стрелок стреляет в мишень. Вероятность выбить 10 очков равна 0,3, а вероятность выбить 9 очков равна 0,6. Чему равна вероятность выбить не менее 9 очков?
Решение. Событие А «выбить не менее 9 очков» является объединением событий В - «выбить 10 очков» и С - «выбить 9 очков». При этом события В и С несовместны, так как нельзя одним выстрелом выбить сразу и 9, и 10 очков.
Поэтому по теореме 1 имеем:
(A)=P(B)+P(C)=0,3+0,6=0.9.
Теорема 2. Для любого события А имеем: 
Пример. Берётся наудачу трёхзначное натуральное число от 100 до 999. Какова вероятность того, что хотя бы две его цифры совпадают?
Решение. Опыт здесь состоит в том, что наудачу выбирается натуральное число от 100 до 999 и смотрят, есть ли у него совпадающие цифры. События «взяли наудачу число N» (N= 100, 101, …, 999) равновероятны (в этом смысл слова «наудачу») и образуют множество исходов этого опыта. Число исходов n=900. Нас интересует событие А - «у выбранного числа совпадают хотя бы две цифры». Проще, однако, подсчитать вероятность противоположного события 
- «у выбранного числа все цифры различны». Каждое такое число есть размещение без повторений из 10 цифр по 3, не имеющее первым элементом нуль. Следовательно, 
(из числа всех трёхэлементных размещений без повторений надо вычесть число тех, у которых на первом месте стоит нуль) и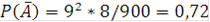 
. Тогда по теореме 2: P(A)=1-P(
)=0,28.
Пример. В урне, содержащей n шаров белого, красного и чёрного цвета, находится k белых шаров и L красных. Какова вероятность вынуть шар не чёрного цвета?
Решение. Если событие А состоит в появлении белого, а событие В - красного шара, то появление шара не чёрного цвета означает появление либо белого, либо красного шара. Так как по определению вероятности
(A)=k/n, P(B)=L/n,
То по теореме сложения вероятность появления шара не чёрного цвета равна:
P(A U B)=k/(n+L)/n=(k+L)/n.
Эту задачу можно решить и так. Пусть событие С состоит в появлении чёрного шара. Число чёрных шаров равно 
, так что
.
Появление шара не чёрного цвета является противоположным событием 
, поэтому на основании указанного выше следствия из теоремы сложения имеем:
, как и раньше.
Пример. В денежно - вещевой лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность какого - либо выигрыша на один лотерейный билет?
Решение. Если обозначить через А событие, состоящее в выпадении денежного выигрыша, и через В - вещевого, то из определения вероятности следует P(A)=120/1000=0,12; P(B)=80/1000=0,08. Интересующее нас событие представляет 
, поэтому из теоремы сложения вытекает:
.
Таким образом, вероятность какого - либо выигрыша равна 0,2.
событие эксперимент эйлер