Так как событие отождествляется с множеством, то над событиями можно совершать все операции, выполняемые над множествами. В частности, определены следующие операции и отношения между событиями.
Событие С, состоящее в наступлении хотя бы одного из событий А и В, называется суммой или объединением событий A и В и обозначается 
или 
.
Суммой или объединением нескольких событий 
называется событие С, состоящее в осуществлении хотя бы одного из событий 
: 
, или 
Пример. Если событие А - появление пяти очков при бросании игральной кости, а В - шести очков, то событие С = А + В - появление не менее пяти очков.
Пример. Опишите, в чем состоит сумма следующих несовместных событий:
) Учитель вызвал к доске ученика (событие А), ученицу (событие В).
) "Родила царица в ночь, не то сына (событие А), не то дочь (событие В):".
) Случайно выбранная цифра меньше 5 (событие А), больше 6 (событие В).
) Из 10 выстрелов в цель попали ровно 7 раз (событие А), не больше 6 раз (событие В).
Решение:
) Учитель вызвал к доске ученика или ученицу (А 
В).
) Царица родила сына или дочь (А 
В).
) Случайно выбранная цифра меньше 5 или больше 6 (А В, то есть это одна из цифр 0,1,2,3,4,7,8,9).
) Из десяти выстрелов в цель попали не более 7 раз (А В, то есть число попаданий 0,1,2,3,4,5,6 или 7 раз).
Ответ: 4 сложных события, являющиеся суммой двух несовместных событий.
Событие С, состоящее в том, что событие А произошло, а событие В не произошло, называется разностью событий A и В и обозначается С = А\В или С = А - В.
Пример. При бросании игральной кости событие А означает выпадение четного числа очков, событие В - выпадение не менее 3 очков (т.е. 3, 4, 5 или 6). Тогда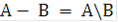 
состоит в выпадении «двойки», 
- в выпадении «тройки» или «пятерки».
Событие С, состоящее в одновременном осуществлении событий А и В, называется произведением или пересечением (совмещением) событий А и В и обозначается 
или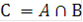 
.
Произведением или пересечением нескольких событий называется событие С, состоящее в одновременном осуществлении событий :
, или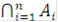 
Пример. Победитель соревнования награждается: призом (событие А), денежной премией (событие В), медалью (событие С). Что представляют собой события: а) А + В, б) ABC, в)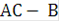 
?
Решение: а) Событие А + В состоит в награждении победителя или призом, или премией, или и тем и другим.
б) Событие ABC состоит в награждении победителя одновременно и призом, и премией, и медалью.
в) Событие 
состоит в награждении победителя одновременно и призом, и премией без выдачи медали
Событие 
означает, что произошло событие В и не произошло событие А.
Событие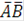 
означает, что ни А, ни В не произошло.
Если событие А не может произойти, если не произошло событие В, т.е. событие А влечет за собой событие В, то пишут А ⊃ В. В этом случае каждая точка события А содержится в событии В. С другой стороны, говорят, что событие В является следствием события А и пишут В ⊃ А.
Если А ⊃ В и В ⊃ А, то события А и В называют равносильными и пишут А = В.
События А и В называют несовместными, если АВ = 
.
События А и В называются противоположными, если 
=В. Очевидно в этом случае 
.
Если I - пространство элементарных событий, то I - А = , I - достоверное событие.
Равенство АВ = ∅ означает то же самое, что и А ⊃ 
и В ⊃ 
.
Событие А - АВ означает, что произошло событие А, не произошли одновременно события А и В. Поэтому 
.
Примеры. 1. Событие А - извлечение из колоды карт карты пиковой масти, событие В - извлечение из колоды дамы. Тогда событие С =АВ - извлечение из колоды дамы пик. 2. Событие 
- выпадение «шестерки» при бросании игральной кости, событие 
- выпадение четного числа очков, а событие 
- выпадение числа очков, большего двух. Тогда 
есть выпадение 2, 3, 4, 5 или 6 очков, а событие 
- выпадение 6 очков.
Для сложения и умножения событий имеют место следующие свойства:
. Коммутативность:
А + В = В + А, АВ = ВА.
. Ассоциативность:
А + (В + С) = (А +В) + С, А(ВС) = (АВ)С.
. Дистрибутивность:
(B + C) =АВ + АС.
Законы де Мо́ргана (правила де Мо́ргана) - логические правила, связывающие пары логических операций при помощи логического отрицания. Открыты шотландским математиком Огастесом де Морганом. Огастес де Морган первоначально заметил, что в классической логике высказываний справедливы следующие соотношения:
Рассмотрим различные способы доказательства законов де Моргана:
1) Аналитический
Событие 
означает, что произойдет хотя бы одно из слагаемых событий А или В. Ему противоположное 
означает, что не произойдет ни А, ни В, т. е. произойдут оба противоположных события 
и вместе, следовательно произойдет их произведение .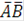
Пример. Используя законы Де-Моргана, произвести двойное отрицание суждения, которое звучит следующим образом:
«Он повернет налево или направо».
Решение. Так как здесь использован союз «или», то это дизъюнкция.
Согласно закону Моргана, отрицание дизъюнкции является конъюнкцией отрицаний:
= 
,
т.е. двойное отрицание суждения «он повернет налево или направо» будет звучать, как «Неверно, что он не повернет налево и не повернет направо».
Пример. Какое логическое выражение равносильно выражению 
) 
) 
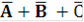
) A + ВС
) А В + С
Решение.
Логические выражения называются равносильными, если при любых значениях, входящих в них переменных, значения этих выражений равны.
Преобразуем выражение 
в соответствии с законом де Моргана: 
,поэтому правилен ответ под номером 1.
Пример. Упростить: 
Решение.
Применим закон де Моргана:
Пример. Упростить: 
Решение. В данном случае воспользуемся законом двойного отрицания.
(раскроем одно отрицание) 
(перемножим первую и вторую скобки, упростим, а третью пока оставим без изменения) 
(перемножим скобки и упростим) 
(раскроем по закону де Моргана) 
Диаграммы Эйлера-Венна
С помощью диаграмм Эйлера-Венна можно геометрически представить операции над множествами событий Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его - кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В:
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В:
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В:
Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В:
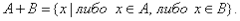
Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А:
Заключение
В ходе выполнения работы, мною было рассмотрено понятие событий и операций над ними. В данных главах я дал определения событий и их типов, указал, какие действия можно совершать над событиями, попутно показав их на диаграммах Эйлера-Венна, на примерах рассмотрел практическое решение вероятностных задач на события.
События и их вероятности практически окружают нас везде и даже невозможно представить, что может быть без их участия. Я думаю, что моя курсовая работа окажется интересным материалом для студентов и преподавателей, которые захотят по своей воле или нет погрузиться в этот загадочный и интересный мир событий теории вероятностей.
Литература
1. Павлов С.В. - Теория вероятностей и математическая статистика
. Новосибирский Государственный Аграрный Университет Инженерный Институт - Учебное пособие Теория вероятностей и математическая статистика
. Гмурман В. Е. - Руководство к решению задач по теории вероятностей и математической статистике. Изд. 3
. https://lvf2004.com - Дискретная математика электронный учебник
. https://ru.wikipedia.org
. Л.В. Рунов - Методические указания по высшей математике ч. 8 по теме: «Алгебра событий»
. Ю.Д. Максимов - Теория вероятностей, детализированный конспект
. В. Н. Студенецкая - Решение задач по статистике, комбинаторике и теории вероятностей.