Министерство образования Российской Федерации
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени А.Н. Туполева
Кафедра общей физики
Лабораторная работа № 91К
ИССЛЕДОВАНИЕ СВОЙСТВ ПОЛУПРОВОДНИКОВЫХ
ТЕРМОЧУВСТВИТЕЛЬНЫХ СОПРОТИВЛЕНИЙ
Казань 2003
ИССЛЕДОВАНИЕ СВОЙСТВ ПОЛУПРОВОДНИКОВЫХ ТЕРМОЧУВСТВИТЕЛЬНЫХ СОПРОТИВЛЕНИЙ
Цель работы: снять вольт-амперную и температурную характеристики полупроводникового термосопротивления; вычислить энергию активации свободных носителей ∆Е и температурный коэффициент термосопротивления α для ряда температур.
Содержание работы
Согласно зонной теории электрические свойства кристаллов определяются структурой энергетических зон.
Чтобы понять происхождение зон, рассмотрим воображаемый процесс объединения атомов в кристалле. Пусть первоначально имеется N изолированных атомов какого-либо вещества. Пока атомы изолированы друг от друга, они имеют полностью совпадающие энергетические уровни. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах. По мере сближения атомов между ними возникает все усиливающееся электромагнитное взаимодействие, которое приводит к изменению положения уровней. Если кратность вырождения энергетического уровня электрона изолированного атома равна α, то вместо одного одинакового для всех N атомов уровня возникают α N очень близких, но не совпадающих подуровней. Таким образом, каждый уровень изолированного атома расщепляется в кристалле на α N густо расположенных подуровней, образующих разрешённую энергетическую зону. Между разрешенными зонами располагаются запрещенные зоны.
|
|
Степень расщепления для разных уровней не одинакова. С ростом электромагнитного взаимодействия сначала снимается вырождение уровней, заполненных внешними электронами атома. Уровни, заполненные внутренними электронами, расщепляются при более сильных полях. С ростом энергии ширина разрешённой зоны увеличивается, а ширина запрещенной зоны уменьшается.
На любом разрешенном подуровне по принципу Паули могут находиться только два электрона, обладающие противоположными ориентациями спинов. Полностью заполненная разрешённая зона, над которой располагаются либо частично заполненная зона, либо полностью свободная зона, называется валентной зоной. Разрешённая зона, расположенная над валентной зоной, называется зоной проводимости.
В зависимости от степени заполнения разрешённых зон электронами и ширины запрещенной зоны возможны три случая, изображенных на рисунке 1.
а) Металл б) Полупроводник в) Изолятор
Рис.1.
В случае а) электроны заполняют зону проводимости не полностью. Поэтому при температуре 0 К энергия теплового движения или приложенного электрического поля достаточна для перевода части электронов на более высокие подуровни (расстояние между подуровнями в зоне порядка 10-22 - 10-23 эВ). Таким образом, электроны зоны проводимости могут ускоряться приложенным электрическим полем. Следовательно, под действием электрического поля возникает электрический ток. Кристалл с подобной схемой энергетических уровней представляет собой проводник. Типичными примерами такой группы являются металлы.
|
|
В случаях б) и в) все уровни валентной зоны заняты электронами. Чтобы электроны получили возможность перемещаться, необходимо сообщить им энергию не менее энергии, равной ширине запрещенной зоны. Тогда часть их переместится в свободную разрешенную зону, а в нижней разрешенной зоне появятся свободные уровни. Если ширина запрещенной зоны порядка нескольких десятых электрон-вольт, то энергия теплового движения достаточна для перевода части электронов в верхнюю свободную зону. В кристалле появляются свободные электроны, число которых быстро растет с ростом температуры. Такое вещество называют полупроводником.
Если ширина запрещенной зоны порядка нескольких электрон-вольт, энергия теплового движения недостаточна для перевода заметного числа электронов на свободную зону. Такое вещество называется диэлектриком. Оно почти не имеет свободных электронов и поэтому не проводит электрического тока.
Итак, мы выяснили, что полупроводниками являются твердые тела, у которых целиком заполненная валентная зона отделена от зоны проводимости не слишком широкой запрещенной зоной (не более 1 эВ).
Поэтому электрическая проводимость полупроводника является возбужденной, т.е. появляется под воздействием лишь внешнего фактора (температура, облучение, поля), который сообщает электронам так называемую энергию активации, равную ширине запрещенной зоны.
Различают собственные и примесные полупроводники. К числу собственных полупроводников относятся химически чистые полупроводники. Электрические свойства примесных полупроводников определяются имеющимися в них искусственно вводимыми примесями.
|
|
При рассмотрении электрических свойств полупроводников большую роль играет понятие «дырок». В собственном полупроводнике при абсолютном нуле все уровни валентной зоны полностью заполнены электронами, а в зоне проводимости электроны отсутствуют. Электрическое поле не может перебросить
∆ Е
Рис.2
электроны из валентной зоны в зону проводимости. Поэтому собственные полупроводники ведут себя при абсолютном нуле как диэлектрики. При температурах, отличных от О К, часть электронов с верхних уровней валентной зоны переходит в результате теплового возбуждения на нижние уровни зоны проводимости. В этих условиях электрическое поле получает возможность изменять состояние электронов, находящихся в зоне проводимости. Кроме того, вследствие образования вакантных уровней в валентной зоне, электроны этой зоны также могут изменять свою скорость под действием внешнего поля. В результате электропроводимость полупроводника становится отличной от нуля. При наличии вакантных уровней поведение электронов валентной зоны может быть представлено как движение положительно заряженных квазичастиц, получивших название дырок.
Термосопротивлениями (термисторами) называются устройства, электрическое сопротивление которых зависит от температуры. Они могут быть изготовлены из металлов и полупроводников. Повышение температуры на 1°С увеличивает электропроводность полупроводника на 3-6%, повышение на 10°С – приблизительно на 75%, а повышение температуры на 100°С увеличивает электропроводность в 50 раз, в то время как для металлов изменение электропроводности при нагревании на 1°С составляет в среднем всего 0,3%. Поэтому термосопротивления из полупроводников более эффективны, чем из металлов.
Проводимость пропорциональна подвижности свободных носителей тока и их концентрации. Удельная проводимость полупроводников складывается из двух составляющих – электронной (γn) и дырочной (γp) и определяется формулой
(1)
Здесь n и p – соответственно – концентрации электронов и дырок;
μn и μp – подвижности электронов и дырок (средняя скорость дрейфа электрона или дырки при напряженности электрического поля, равной единице). В собственных полупроводниках концентрации электронов и дырок одинаковы (n=p), так как каждому электрону в зоне проводимости соответствует дырка в валентной зоне. Поэтому формула (1) может быть упрощена
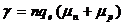(2)
Подвижности электронов и дырок различны. Для большинства полупроводников μn > μр.
В металлах концентрация электронов проводимости не изменяется с изменением температуры. Поэтому температурная зависимость электропроводности металлов определяется исключительно подвижностью электронов. При нагревании металла возрастает амплитуда тепловых колебаний атомов решетки. В результате вероятность рассеяния электронных волн при взаимодействии с колеблющимся полем решетки увеличивается и подвижность электронов уменьшается. Поэтому при нагревании сопротивление металлов возрастает по закону:
R=R0(1 + αt°). (3)
Температурный коэффициент сопротивления металлов α положителен и остается почти постоянным при изменении температуры.
В отличии от металлов концентрация свободных носителей в полупроводниках меняется с температурой.. Температурная зависимость концентрации свободных носителей заряда для собственных полупроводников выражается формулой
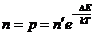(4)
где n′ - множитель, медленно изменяющийся с температурой по сравнению с экспоненциальным множителем; ∆Е – энергия активации.
Зависимость подвижности носителей в полупроводниках от температуры описывается формулой
(5)
где a и b – постоянные для данного вещества коэффициенты. Подставляя выражение для n, p и μ из (4) и (5) в формулу (1), определяющую проводимость полупроводника, можно увидеть, что температурный ход проводимости определяется в основном экспоненциальным множителем 
. Таким образом, концентрация носителей заряда растет с повышением температуры значительно быстрее, чем убывает подвижность, и проводимость полупроводника возрастает с повышением температуры.
Зависимость проводимости беспримесных полупроводников от температуры можно представить в виде:
(6)
Коэффициент γ0 представляет собой максимальную проводимость полупроводника, возникающую при такой температуре, при которой будут ионизированы все атомы полупроводника.
Для примесных полупроводников температурная зависимость проводимости может быть выражена формулой
(7)
где первое слагаемое соответствует собственной проводимости, а второе слагаемое представляет собой вклад примесной проводимости. Здесь ∆Eпр – энергия активации валентных электронов примеси, g1 проводимость полупроводника при полной ионизации атомов примеси. В области низких температур преобладает примесная проводимость. При возрастании температуры полупроводника возбуждается собственная проводимость, которая быстро растет с увеличением температуры за счет возрастания концентрации собственных носителей тока. С увеличением примеси температура перехода от примесной проводимости к собственной смещается в сторону высоких температур.
Зная зависимость удельной проводимости полупроводника от температуры, можем найти характер изменения электрического сопротивления полупроводникового термистора, что удобно при расчетах электрических цепей с термосопротивлениями. Зависимость удельного сопротивления полупроводника от температуры выражается функцией:
(8)
где 
- коэффициент, зависящий от физических свойств полупроводника. Тогда электрическое сопротивление термистора выразится формулой:
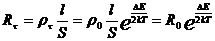(9)
где l и S – длина и площадь поперечного сечения термосопротивления; 
- сопротивление термистора при полной ионизации атомов полупроводника.
Для характеристики температурной зависимости сопротивления проводников вводится температурный коэффициент сопротивления:
. (10)
Подставляя в формулу (10) выражения для Rτ и 
, получим
. (11)
Знак минус указывает на то, что электрическое сопротивление полупроводниковых термисторов уменьшается с повышением температуры.
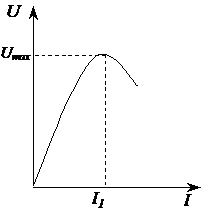
Рис. 3
Полупроводниковые термосопротивления являются нелинейными элементами. Типичная вольт-амперная характеристика термистора изображена на рис.3, где по оси ординат откладываются значения напряжения U на термосопротивлении, а по оси абсцисс – значение тока I, проходящего через термистор.
Линейность начального участка объясняется тем, что при малых токах мощность, идущая на нагревание термосопротивления, мала, и, следовательно, его температура не настолько велика, чтобы вызвать заметное изменение сопротивления. При дальнейшем увеличении тока мощность становится значительной, температура термосопротивления повышается и электрическое сопротивление уменьшается. Поэтому крутизна вольт-амперной характеристики убывает. Начиная с некоторого значения тока I′ сопротивление термистора убывает настолько быстро, что несмотря на увеличение силы тока через термосопротивление, напряжение на нем падает.
Запишем формулу (9) для двух различных температур Т1 и Т2 .
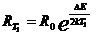
Разделив первое выражение на второе, получим
(12)
Прологарифмировав выражение (12), найдем:
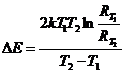(13)
Таким образом, измерив сопротивление термистора при двух различных температурах Т1 и Т2, и, воспользовавшись формулой (13), можем вычислить энергию активации свободных носителей. Зная величину ∆Е для данного термосопротивления и его сопротивление при температуре Т, при помощи формулы (13) можем вычислить сопротивление термистора при любой температуре.
Описание установки
Для выполнения работы собрана лабораторная установка, схема которой представлена на рис.4. Включение установки в сеть осуществляется при помощи ключаК1. Исследуемое термосопротивление ТС включено в цепь постоянного тока, получаемого от выпрямителя В1. Величину тока, протекающего через термосопротивление, можно менять путем перемещения контакта D сопротивления R1 и определять по миллиамперметру мА. Падение напряжения на термосопротивлении измеряют вольт-метром V. С изменением величины тока, проходящего через термосопротивление, будет меняться и падение напряжения на нем. Задавая определенное значение тока и определяя падение напряжения на термосопротивлении, можем получить вольт-амперную характеристику термистора.
Рис.4. Принципиальная схема установки
Для изменения температуры термистора в установке используется нагреватель, представляющий собой остеклованное сопротивление R2, помещенное в металлический кожух К. Нагреватель при помощи ключа К2подключается к источнику питания 24 В. Температуру термистора измеряют лабораторным термометром Т.
Порядок выполнения работы
1. Начертить в тетради таблицы 1 и 2.
.
Таблица 1
| № изм. | Т1,К | Т2,К | ||
| I, мА | U, В | I, мА | U, В | |
Таблица 2
| № изм. | U, B | Т, К | при повышении T | при понижении T | Rс р, кОм | ||
| I, мА | R, кОм | I, мА | R, кОм | ||||
2. Включить компьютер.
3. Запустить программу lab91. Для этого указать курсором на lab91 и щелкнуть левой кнопкой мышки (в дальнейшем эту команду обозначим L’ на lab91).
Ввести значения D Е, размеры a, b и c. ОК. Значения D Е, размеры a, b и c записать в тетради. Изучить информацию на экране. Вверху слева показаны миллиамперметр, вольтметр, ниже ползунок для перемещения контакта D, термометр и правее подсказки и таб. 1.
Снятие ВАХ термосопротивления
4. Путем перемещения ползунка резистора установить значения U, указанные в таб.1, и записать значения I. Поставить ползунок резистора в крайнее левое положение.
5. Включить нагрев и поднять температуру до 40 0С. Зафиксировать температуру клавишей Зафикс.
5.Повторить пункт 4.
Снятие температурной характеристики термосопротивления
6. Поставить ползунок резистора в крайнее правое положение.При этом будет U= 10 B.
7. Включить нагрев и поднять температуру до 30 0С. Зафиксировать температуру клавишей Зафикс. Записать значения I и Т, определить сопротивление термистора.
8. L’ на Отмена и после повышения температуры на 5 0С L’ на Зафикс. Записать значения I и Т, определить сопротивление термистора.
9. Повторить пункт 8 еще 12 раз, повышая температуру каждый раз на 5 0С.
Для каждого значения температуры определить Rс р .
10. Далее провести измерения I и Т при тех же температурах в процессе охлаждения термистора.
11. По полученным значениям Rср вычислить 3 значения энергии активации свободных носителей ∆Е для различных температур по формуле (13). Найти среднее значение энергии активации ∆Еср в электрон-вольтах. Вычислить температурный коэффициент сопротивления термистора αт по формуле (11).
10. Построить график зависимости ατ от температуры. Объяснить полученные результаты.
11 .L’ на Выход.
Контрольные вопросы
1. Что такое энергия активации?
2. Пояснить механизм возбуждения проводимости полупроводника.
3. Что такое термосопротивление?
4. Как изменяется проводимость полупроводников с изменением температуры?
5. Как определяется температурный коэффициент сопротивления для полупроводников?
6. Как можно экспериментально определить энергию активации?