Лекция №18
Тема: «Изгиб»
Вопросы:
Касательные напряжения при поперечном изгибе
Центр изгиба
Главные напряжения при изгибе. Линии главных площадок
Касательные напряжения при изгибе
При поперечном изгибе помимо изгибающего момента М в сечении возникает поперечная сила Q, которая вызывает касательные напряжения. Для их определения рассмотрим верхнюю часть отрезка балки (см. рис. 1), длиной dz: от линии m-n.
Рис. 1
В левом сечении будут возникать нормальные напряжения:
в правом:
.
В сечении m-n будут возникать касательные напряжения. Для определения их величины рассмотрим условие статического равновесия кусочка балки относительно оси Z.
или
.
Разность значений моментов на бесконечно близком расстоянии один от другого представляет собой дифференциал момента dM, а 
- статический момент заштрихованной части сечения, образуемой верхней частью сечения до линии m-n (отсеченной частью сечения) относительно оси X.
где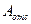 
- площадь заштрихованной части сечения.
Тогда:
или
.
Первая производная от момента по Z равна поперечной силе Q, поэтому получим окончательную формулу:
. (1)
Согласно закону парности касательных напряжений, касательные напряжения в поперечных сечениях по линии m-n будут равны касательным напряжениям в продольном сечении, определяемым по формуле (1). Из формулы видно, что касательные напряжения прямо пропорциональны 
. Определим характер изменения касательных напряжений по высоте сечения для прямоугольного профиля. Пусть рассматриваемая точка В лежит на расстоянии Y от оси X. Через точку В проводим прямую, параллельную оси X (см. рис. 1). Эта прямая рассекает сечение на мне части, статические моменты которых относительно оси X равны, так что безразлично какую часть сечения рассматривать.
|
|
Рис. 2
Будем рассматривать верхнюю (заштрихованную) часть. Статический момент любой фигуры равен произведению площади на координату центра тяжести.
,
где =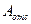 
.
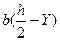
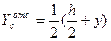В результате получим:
,
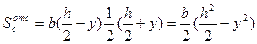т.е. изменяется по закону параболы, так как Y во второй степени. Поскольку между t и прямая пропорциональность, то и эпюра t будет изменяться по высоте по закону квадратичной параболы. При 
; =0 и t=0. Наибольшее значение будет при y=0, поэтому наибольшие касательные напряжения будут возникать на нейтральной линии.
У двутаврового сечения характер распределения касательных напряжений будет следующий (см. рис. 3). Резкий скачок на эпюре t в месте перехода полки к стенке вызван резким уменьшением ширины сечения b, входящей в знаменатель формулы (1). Касательные напряжения, возникающие в полках незначительны по сравнению с возникающими в стенке, и ими обычно игнорируют. Поэтому эпюру t изображают без этих участков (показано справа).
Рис. 3
Наибольшие касательные напряжения, возникающие в нейтральном слое, сравнивают с расчетным сопротивлением на срез Rs:
.
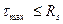Центр изгиба
Для балок целесообразно применять тонкостенные профили с развитыми горизонтальными полками и тонкой стенкой. Такие профили обычно изготавливают прокаткой или гибкой из листовой заготовки. При этом особенно технологичны профили с одной осью симметрии, например, швеллер (см. рис. 4, а).
При поперечном изгибе в стенке возникнут касательный напряжения 
, определяемые но формуле (1), и эпюра представляет параболу. В полках тоже будут возникать касательные напряжения. Их можно определить таким же путем, делая вертикальные разрезы полки. Эпюра касательных напряжений 
представляет треугольник. Касательные напряжения в верхней и нижней полках направлены в разные стороны и будут создавать момент, подвергающий сечение скручиванию (см. рис. 4, б). Его можно исключить, если внешнюю силу приложить в точке С. Из условия равенства моментов, определим расстояние а, на котором нужно приложить внешнюю силу:
|
|
,
где Т - усилие, возникающее в полках от напряжения ,
t - толщина полки,
h - высота профиля.
. (2)
Рис. 4
Главные напряжения при изгибе
При поперечном изгибе в поперечных сечениях возникают нормальные и касательные напряжения, определяемые по формулам:
; и 
.
В продольном сечении нормальные напряжения отсутствуют, а касательные равны касательным напряжениям в поперечном сечении (закон парности касательных напряжений).
Поэтому элемент будет иметь вид (см. рис. 5).
Главные напряжения определяют по формуле:
.
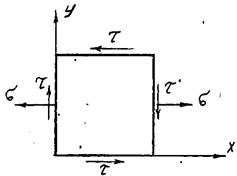
Рис. 5
В данном случае:
.
Главные напряжения имеют индексы:
, поэтому:
.
Положение главной площадки определяют по формуле:
.
Вторая главная площадка будет перпендикулярна найденной.
Исследуем напряженное состояние в тpex точках, лежащих в одном и том же поперечном сечении, но взятых на разной высоте (см. рис. 6), а именно: в верхнем сжатом волокне (точка 1), в нейтральном слое (точка 2) и в нижнем растянутом волокне (точка 3).
В точке 1:
|
|
;
,
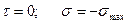вторая площадка перпендикулярна, следовательно, 
В точке 2: 
.
Если на площадках действуют только касательные напряжения, то это чистый сдвиг.
,
следовательно: 
.
Рис. 6
В точке 3: 
;
.
Вычисляя главные напряжения для целого ряда точек какого-либо поперечного сечения, можно построить эпюры 
и 
и определить углы, под которыми расположены главные площадки.
Скачки в эпюрах и объясняются наличием скачка в эпюре 
в месте перехода полки к стенке. В этих местах и зачастую превышают 
. Это обстоятельство обязательно должно быть учтено при проверке прочности двутавровых балок.
Наглядное представление о потоке внутренних сил в нагруженном теле дают траектории главных напряжений. Так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке.