С целью определить закономерности в серии случайных событий выигрыша или проигрыша в игре орел или решка проанализированы результаты более 100 тыс. игр сериями по 50, 100, 200 игр. Результат типичной игры представлен на рисунке 1.

Рис. 1
Сначала была тенденция к проигрышу, потом к выигрышу, окончательный результат 11, к примеру, рублей. Линия результатов игры представляет собой ломаную линию.
Корреляция выигрыша производилась с ломаными и прямыми линиями. Ломаные линии циклические, возрастание сменяется снижением. Номер линии означает максимальное значение, период роста и снижения. Ломаные линии напоминают волны, и номер линии соответствует половине длины волны. Первые 10 ломаных представлены на рис. 2.

Рис. 2
Корреляция линии результатов приведенной выше игры с ломаными разных полупериодов представлена на рисунке 3.

Рис. 3
Ряд 2 это R квадрат, ряд 1 его критическое значение. Здесь наибольшее значение корреляции при полупериоде 100, что отражает общую тенденцию игры к выигрышу, также достоверная корреляция наблюдается при полупериодах 41, 27, и 18.
Игры получаются разные и линии корреляции разные, но циклические и очень красивые.
Повторение серий игр сто раз и вычисление среднего R квадрата показывает закономерность зависимости его от полупериода ломаной (рис. 4).

Рис. 4
Зависимость носит циклический характер и напоминает синусоиду с растущей амплитудой колебаний.
Если свести 50, 100, 200 игр к одному знаменателю, то линии практически совпадают. То есть корреляция зависит от места в периоде игры (рис. 5).

Рис. 5
Чем больше играешь, тем больше вероятность выигрыша или проигрыша, но вероятность растет циклически. Цикличность достоверна, стабильна, но не играет большой роли, меньше 5% отличия от прямой линии.
С одними линиями получается положительная корреляция, с другими отрицательная (рис. 6).

Рис. 6
Где предпоследний отрезок направлен вверх, там положительная корреляция и наоборот. Линии с положительной и отрицательной корреляцией находятся в противофазе.
Почему-то, для максимальной корреляции необходим небольшой снижающийся или повышающийся последний отрезок. На рисунках 7 и 8 максимальная корреляция выигрыша с линией 29, а не с линией 33, заканчивающейся на максимуме роста. Это трудно объяснить, но это свидетельствует о важности фазы, в которой ломаная линия приходит к концу игры. Объяснение заключается в линиях тренда ломаных.

Рис. 7

Рис. 8
На рис. 7 видно увеличение наклона линии тренда от 25 до 29 линии, а на рис. 8 снижение от 30 до 33 линии. Снижение наклона линии тренда будет продолжаться до 42 линии, затем наклон будет увеличиваться. Динамика наклона является циклической с нарастанием амплитуды колебаний. До 50 линии наклон поочередно принимает положительные и отрицательные значения, после только положительные. Коэффициент корреляции выигрыша прямо связан с наклоном линии тренда ломаной.
Коэффициент корреляции также зависит от динамики конечного значения ломаной: при положительной динамике он максимальный, при отрицательной минимальный (рис. 9).

Рис. 9
Зависимость нелинейная. Максимальные и минимальные значения R находятся на середине отрезков роста или снижения.
Зависимость R от динамики конечного значения ломаной является параболической (рис. 10 и 11).

Рис. 10
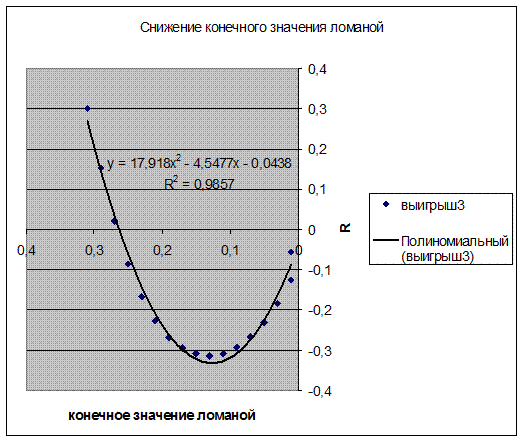
Рис. 11
Таким образом, выигрыш достоверно циклически зависит от длины волны и частоты колебания ломаной и от конечной фазы, в которой ломаная линия приходит к концу серии игр. Коэффициент корреляции выигрыша прямо связан с наклоном линии тренда ломаной, который циклически изменяется. Зигзаг удачи существует, одни частоты имеют положительное значение, другие отрицательное. Ломаные циклично коррелируют с 100 линией (линией только роста) и выигрыш повторяет эту корреляцию (рис. 12).

Рис. 12
Линии 12 и 13 имеют циклическую корреляцию с линией роста (рис. 13).

Рис. 13
Фазы линий с ростом числа игр сдвигаются, переходя в противофазу, дальше могут опять совпадать по фазе и т.д.

Рис. 14
Соответственно результаты игры сначала имеют одинаковую корреляцию, затем противоположную, потом снова в одной фазе (рис 14). Но значение R у линий 12 и 13 могут значительно различаться.
Соотношение коэффициента корреляции результатов игры с линиями 12 и 13 показаны на рисунках 15, 16, 17.

Рис. 15

Рис. 16

Рис. 17
Красивые рисунки, напоминающие объекты космоса или микромира. Но это предмет другого исследования - сочетания порядка и хаоса.
Корреляция выигрыша с прямой роста представлен на рис. 18.

Рис. 18
На рисунке видны крайне изменчивые значения R. Если вычислить средний R квадрат у нескольких серий игр, получится следующая картина (рис. 19).

Рис. 19
Усреднение не показывает никакой закономерности в динамике R квадрата. В каждой линии результат миллиона игр. Если взять 2000 игр, то динамика R квадрата также совершенно непредсказуема (рис. 20).

Рис. 20
R квадрат совершенно случайным образом колеблется у своего среднего значения 0,44, полученного при анализе результатов 6 млн. игр. И сколько ни проводится игр, результаты получаются совершенно разные и непредсказуемые. Так обстоит дело с корреляцией случайных чисел с прямой. Корреляция с циклическими ломаными объясняется свойствами самих ломаных. Сочетание корреляции выигрыша с прямой и ломаными представлено на рис. 21.

Рис. 21
На фоне непредсказуемой общей тенденции, определяемой прямой, хорошо видны волны циклических колебаний, обусловленные ломаными.