Гармонические колебания
№1. Построить графики простых гармоник:
а) 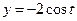 ; б)
; б) 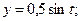 в)
в) 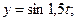 г)
г) 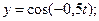 д)
д) 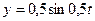 ;
;
е) 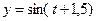 ; ж)
; ж) 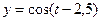 .
.
№2. Построить графики сложных гармоник:
а) 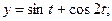 б)
б) 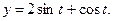
Пределы.
№1. Вычислить пределы:
а) 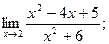 б)
б) 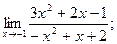 в)
в) 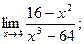 г)
г) 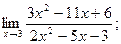 д)
д) 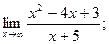
е) 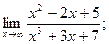 ж)
ж) 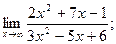 з)
з) 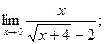 и)
и) 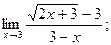 к)
к) 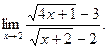
№2. Вычислить, используя замечательные пределы:
а) 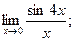 б)
б) 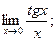 в)
в) 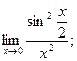 г)
г) 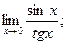 д)
д) 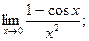 е)
е) 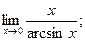
ж) 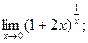 з)
з) 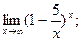 и)
и) 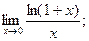 к)
к) 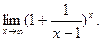
Производная.
№1. Найти производные функций:
а) 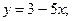 б)
б) 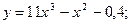 в)
в) 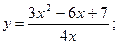 г)
г) 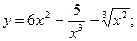
д) 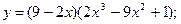 е)
е) 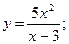 ж)
ж) 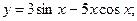 з)
з) 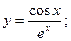 и)
и) 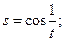
к) 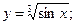 л)
л) 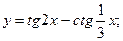 м)
м) 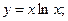 н)
н) 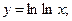 о)
о) 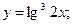 п)
п) 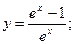
р) 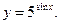
№ 2. Установлено, что энергия, отдаваемая электрическим элементом, определяется по формуле 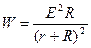 , где Е – ЭДСэлемента, r – внутреннее
, где Е – ЭДСэлемента, r – внутреннее
сопротивление элемента, R – внешнее сопротивление. Каким должно быть сопротивление цепи, чтобы энергия W была наибольшей?
№7 Тело движется прямолинейно по закону 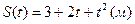 . Определить его скорость и ускорение в момент времени
. Определить его скорость и ускорение в момент времени 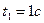 и
и 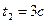 .
.
№3 Тело движется по закону 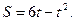 В какой момент времени скорость его окажется равной 0?
В какой момент времени скорость его окажется равной 0?
№4 Тело, масса которого 0,5 кг, движется прямолинейно по закону
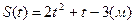 . Найти кинетическую энергию тела через 7с после начала
. Найти кинетическую энергию тела через 7с после начала
движения.
№5 Найти величину силы F, действующей на тело массой 3кг, движущегося по закону 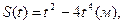 при t = 3с.
при t = 3с.
№6 Количество электричества, протекающего через проводник, начиная с момента времени t = 0, даётся формулой 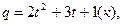 Найти силу тока в конце 5 секунды.
Найти силу тока в конце 5 секунды.
Интеграл
№1 Найти дифференциал функции:
а) 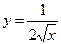 в точке
в точке 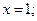
б) 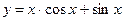 в точке
в точке 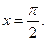
№2 Найти неопределённые интегралы:
а) 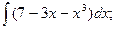 б)
б) 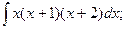
в) 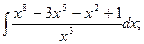 г)
г) 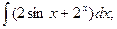 д)
д)  е)
е) 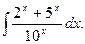
№3 Найти неопределённые интегралы методом подстановки:
а) 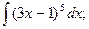 б)
б) 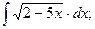 в)
в) 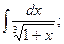 г)
г) 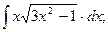
д) 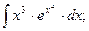 е)
е) 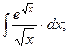 ж)
ж) 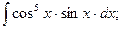 з)
з) 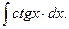
№4 Вычислить интегралы:
а) 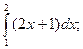 б)
б) 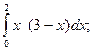 в)
в) 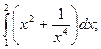 г)
г) 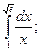 д)
д) 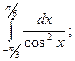
е) 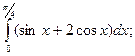 ж)
ж) 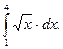
№5 Вычислить интегралы, используя подстановку:
а) 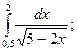 б)
б) 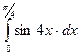 в)
в) 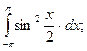 г)
г) 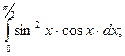
д) 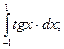 е)
е) 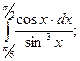 ж)
ж) 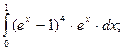
з) 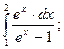 и)
и) 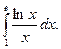
№6. Вычислить методами прямоугольников, трапеций и Симпсона определенные интегралы:
|
|
а) 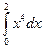 ; б)
; б) 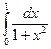 (n=10).
(n=10).
Основные понятия комбинаторики
№1. Вычислить:
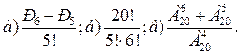
№2. Сколько различных перестановок можно образовать из букв следующих слов:
а) баран; б) абракадабра?
№3. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 5 уроков: алгебра, геометрия, история, география и литература, причем алгебра и геометрия не должны следовать непосредственно друг за другом?
№4. Найдите п, если
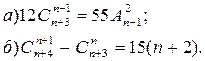
№5. Найдите область определения функции
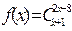
и множество ее значений.
№6. В группе 30 студентов. Сколькими способами можно выделить
2-х человек для дежурства, если
а) один из них должен быть старшим;
б) старшего быть не должно?
№7. В розыгрыше первенства по футболу было сыграно 153 матча. Каждые две команды встречались между собой один раз. Сколько команд участвовало в розыгрыше первенства?
Вероятность события.
№1. По мишени производится два выстрела. Образуют ли события А (мишень поражена) и В (по крайней мере один выстрел был неудачным) полную систему событий? Являются ли события А и В несовместными?
№2. Укажите три события, которые не являются попарно несовместными, но образуют полную систему событий.
№3. Из урны, в которой находятся 3 белых, 4 черных, 5 красных шаров, наудачу вынимается один. Какова вероятность того, что вынутый шар окажется
а) белым; б) черным; в) желтым; г) красным?
№4. Бросаются две игральные кости. Какова вероятность того, что сумма очков, выпавших на двух костях, окажется равной 8?
№5. В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что среди первых пяти наугад выбранных билетов два будут выигрышными?
|
|
Основные теоремы теории вероятностей и их следствия.
1) Докажите, что если события А и В независимы, то и события А и 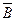
также независимы.
2) Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8 производят по одному выстрелу. Определите вероятность:
а) хотя бы одного попадания в мишень;
б) одного попадания в мишень.
3) Рабочий обслуживает 3 станка, каждый из которых работает независимо от двух других. Вероятности того, что за смену станки не потребуют вмешательства рабочего, равны соответственно
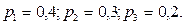
Найдите вероятность того, что за смену по крайней мере один станок потребует вмешательства рабочего.
4) Найти вероятность того, что наудачу взятая кость из игры домино содержит не менее 4 и не более 6 очков
5) Бросается монета до 1-го появления «герба». Найти вероятность того, что потребуется четное число бросков.