9.1. Возрастание энтропии - II начало термодинамики.
Пусть неравновесная замкнутая система обладает энергией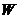 
. Разобьем эту систему на квазизамкнутые макроскопические подсистемы с энергиями 
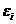. Тогда
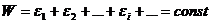. (5.49)
Малые подсистемы достигают равновесия быстрее, чем большие. Поэтому возможна ситуация, когда каждая из малых подсистем достигла своего равновесия, но между подсистемами равновесия еще нет. Большая система при этом не равновесна.
Макроскопическое состояние каждой квазизамкнутой равновесной подсистемы реализуется с вероятностью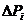 
, которая может быть выражена через энтропию этой подсистемы 
.
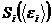Для любой i -ой подсистемы фазовый объем связан с энтропией (безразмерной) выражением:
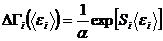. (5.43)
Отсюда следует, что вероятность нахождения малой подсистемы в макроскопическом состоянии с энергией в интервале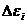 
вблизи 
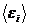, пропорциональная 
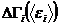, пропорциональна
.
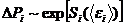Рассматриваемое состояние всей неравновесной системы описывается вероятностью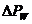 
, которая находится по теореме об умножении вероятностей как произведению всех :
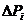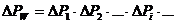(5.50)
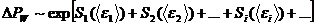. (5.51)
Здесь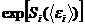 
– быстро меняющаяся функция энергии 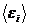, а все остальные опущенные множители меняются слабо с энергией, и на фоне резкой экспоненциальной зависимости их можно считать постоянными.
Нас интересует процесс установления равновесия между подсистемами, приводящий замкнутую систему в равновесие. Поэтому средние энергии подсистем 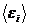мы рассматриваем как переменные, по которым устанавливается равновесие между подсистемами. Из выражения (5.51) следует, что наиболее вероятное равновесное состояние системы достигается при максимальном значении суммы энтропий подсистем, стоящих в показателе экспоненты. Т. о., если суммарная энтропия растет, то соответствующая вероятность 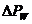растет очень быстро.
|
|
Мы уже обсуждали, что в рамках классической термодинамики нельзя получить информацию о скорости достижения равновесия (т.е. нельзя найти время релаксации). Однако, как в термодинамике, так и статистической физике, удается установить общее направление процессов, которое приводит к росту вероятности реализации макросостояния. Процессы, связанные с уменьшением энтропии, маловероятны, т.к. 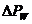резко (по экспоненте) убывает.
Вывод: если замкнутая макроскопическая система находится в неравновесном состоянии, то наиболее вероятным следствием для нее будет монотонное возрастание энтропии.
Закон возрастания энтропии для замкнутых систем – это второе начало термодинамики:
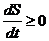. (5.52)
Второе началобыло введено сначала Клаузиусом, а затем вероятностное толкование закона возрастания энтропии было дано Больцманом (1870).
Здесь уместно процитировать Больцмана: всегда имеются флуктуационные состояния, соответствующие уменьшению энтропии, и поэтому чрезвычайно маловероятные. Вероятность их настолько мала, что для макроскопических тел эти флуктуации не наблюдаются.
Во всех имеющихся в природе замкнутых системах энтропия никогда самопроизвольно не убывает, она увеличивается или остается постоянной 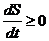. Закон возрастания энтропии (5.52) устанавливает определенное направление течения процессов в природе.
9.2. Обратимые и необратимые процессы.
Основываясь на законе возрастания энтропии все процессы, протекающие в макроскопических телах можно
|
|
разделить на две группы.
1) Процессы, сопровождающиеся возрастанием энтропии замкнутой
неравновесной системы, называются необратимыми.
Для таких процессов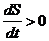 
. Текущие в обратном направлении процессы
оказываются практически невозможными, т.к. они связаны с уменьшением энтропии.
Пример. Расширение газа в пустоту.
|
Пусть в одной половине сосуда, разделенного перегородкой, находится
газ, а вторая половина сосуда вакууммирована. Если убрать перегородку, газ распространится на весь объем. В результате увеличения объема, занимаемого газом, увеличится число микроскопических состояний, реализующих любое из макроскопических состояний газа, т.е. энтропия возрастет. Самопроизвольный обратный процесс, при котором все молекулы газа соберутся в одной половине сосуда, практически невозможен, т.к. ему соответствует упорядоченное движение молекул газа в одну сторону, т.е. уменьшение беспорядка, ведущее к уменьшению энтропии.
Необратимыми являются все процессы в телах, сопровождающиеся потерями энергии на теплообмен с окружающей средой.
Примеры: процессы с трением, выделением джоулева тепла (ток идет через сопротивление), передача тепла от более горячего к более холодному.
2) Процессы, в которых энтропия замкнутой системы остается постоянной во времени, называются обратимыми.
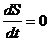. (5.53)
Квазистатические процессы – процессы бесконечно медленно протекающие
во времени, так что в каждый момент времени система находится в равновесии.
Поскольку в равновесном состоянии энтропия системы максимальна, то она и не
изменяется в ходе процесса.
|
|
Поэтому возможен квазистатический процесс, текущий в обратном направлении.
Пример квазистатического процесса: медленное движение поршня в цилиндре
с газом. Можно вернуть систему в исходное
состояние, проходя ту же последовательность
равновесных состояний.
Идеальные квазистатические процессы, естественно невозможно реализовать, поскольку всегда имеются потери, связанные, например, с трением или другими причинами. Тем не менее, представление об идеализированных квазистатических процессах очень важно, т.к. дает возможность правильного качественного, а зачастую и с хорошим приближением количественного описания состояния газа, используя малое число параметров –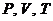 
.
Если замкнутая система образована телом и окружающей его средой, то энтропия системы определяется как
.
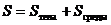В ходе квазистатического процесса энтропия тела может убывать, но при этом энтропия среды должна возрастать так, чтобы суммарная энтропия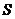 
системы была постоянной:
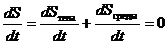. (5.54)
Квазистатический процесс можно реализовать и в теплоизолированном теле, в котором изменение состояния тела происходит под действием внешних сил. Такие процессы называются адиабатическими. Для адиабатических процессов
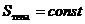или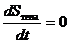 
.
Поскольку нет теплообмена, не происходит и изменения энтропии. Реализация адиабатического процесса трудна, т.к. он должен быть достаточно медленным, чтобы удовлетворять условию квазистатичности, а с другой стороны - достаточно быстрым, чтобы исключить теплообмен с окружающей средой.