Дано: Расчетная схема на рисунке 1.
 |
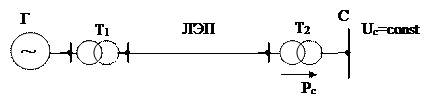Рисунок 1
Элементы схемы имеют следующие данные, например:
Генератор Г: Sгн = 353 (МВА)
Uгн = 20 (кВ)
соsφн =0,85
хd = 2,195 (о.е.) при номинальных базисных условиях.
Трансформатор Т1: SТ1 = 400 (МВА)
U1/ U2 = 20/347 (кВ)
и к1 =11,5 %
Линия эл.передачи ЛЭП: ℓл = 275 км (двухцепная)
х0 = 0,325 Ом/км
Трансформатор Т2: SТ2 = 400 (МВА)
Uв/ Uс = 330/165 (кВ)
и к1 =11 %
Система С: Uс = U = соnst, f с = соnst, U = 155 (кВ)
(бесконечно большой мощности)
Режим нагрузки передающей системы задан величиной активной мощности, передаваемой в приемную систему С.
Рс = (0,8 – 0,95) Рн.г
где Рн.г = Sнг · соsφн – номинальная мощность генератора.
Наряду с мощностью Рс задается и коэффициент мощности соsφс≈ 0,95.
Требуется:
1. Рассчитать параметры схемы замещения эл.системы (простой передачи) в о.е.
2. При заданном режиме нагрузки системы и параметрах схемы замещения построить векторную диаграмму режима, и изобразить характеристику мощности (предварительно определив ЭДС генератора Е).
3. По характеристике мощности найти точку совместной работы генератора и турбины, запас статической устойчивости, предел мощности передачи.
Решение:
1. Расчетная схема разбивается на ступени напряжения по линии
трансформаторов или автотрансформаторов, рисунок 2.
 |
Рисунок 2
2. Расчет ведем в относительных единицах при базисных условиях, общих для всей системы.
Базисная мощность Sб выбирается равной полной мощности одного из элементов: генератора, трансформатора (любого), или близкая круглая цифра (МВА): Sб = 400 МВА.
3. Одну из ступеней напряжения выбираем за основную. На рисунке 2 за основную принята ступень напряжения системы С. Напряжения системы Uс = соnst берется как базисное напряжение UбI = Uс ступени на стороне системы: UбI = 155 кВ.
|
|
Базисное напряжение ступени II.
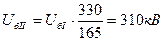
Базисное напряжение генераторной ступени
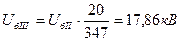
4. В соответствии с формулой
,
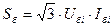где i = I, II, III, находим базисные токи ступеней:
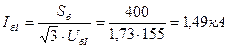
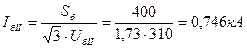
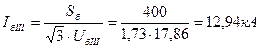
5. В соответствии с формулой
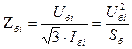
где i = I, II, III, находим базисные сопротивления ступеней
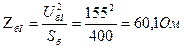
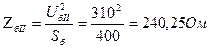
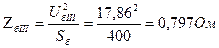
6. При построении схемы замещения принимаем допущения:
- активными сопротивлениями всех элементов схемы пренебрегаем ввиду их малости;
- генератор представляем идеальным источником ЭДС Е за сопротивлением х d;
- трансформаторы и линии замещаем реактивными сопротивлениями х г и х л (индуктивными).
Схема замещения изображена на рисунке 3.
 |
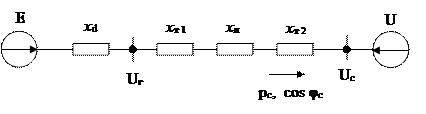Рисунок 3
7. Режим загрузки системы определяем через активную и реактивную мощности, поступающие в приемную систему в о.е.:
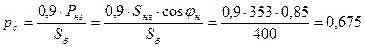
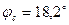
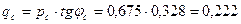
или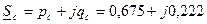 
8. По величине мощности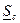 
находим ток 
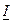. Используем формулу:
,
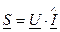откуда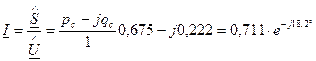 
где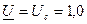 
о.е.
9. Расчет сопротивления генератора х d в о.е. при принятых базисных условиях
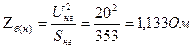
Тогда истинное значение сопротивления генератора в омах:
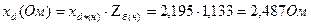
Разделим это сопротивление на базисное сопротивление III-й ступени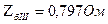 
, получим пересчитанное значение для принятых базисных условий системы в о.е.
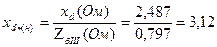
Все расчеты можно записать в виде одной формулы:
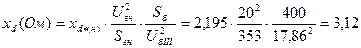о.е.
10. Расчет сопротивлений трансформатора x Т
Основным параметром, определяющим сопротивление трансформатора, является напряжение короткого замыкания u k в о.е. при номинальных условиях трансформатора.
Напряжение короткого замыкания в вольтах
|
|
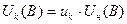
где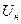 
- номинальное напряжение. При напряжении 
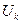(В) и замкнутой вторичной обмотке ток в обеих обмотках равен номинальному (условие оператора КЗ). Тогда сопротивление трансформатора в омах
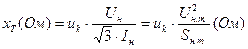
Базисное сопротивление трансформатора при его номинальных условиях
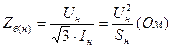
Сопротивление трансформатора в о.е. при номинальных базисных условиях
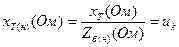
равно напряжению короткого замыкания в о.е. Для принятых базисных условий это сопротивление в о.е. получим, деля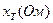 
на 
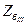или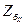 
(Ом). Расчетная формула имеет вид:
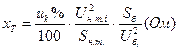
Для трансформатора Т1 (о.е.)
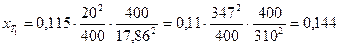
Для трансформатора Т2 (о.е.)
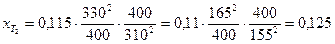
11. Сопротивление линии передачи (ЛЭП) в о.е. одной цепи:
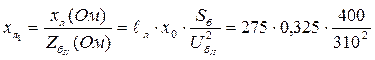
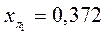
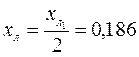
12. Общее сопротивление передающей системы от идеального источника ЭДС Е (в о.е.)
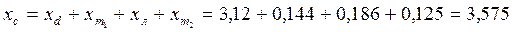
13. Упрощенная схема замещения показана на рисунке 4
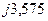
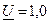
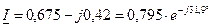
Рисунок 4
14. Уравнение по второму закону Кирхгофа
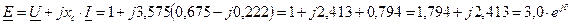
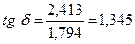
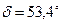
Угол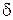 
- есть угол между ЭДС Е и напряжением U = U =1,0
15. Построение векторной диаграммы.
На векторной диаграмме строятся векторы ЭДС Е генератора, напряжение U приемной системы, а также вектор разности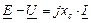 
, представляющий потери напряжения от тока 
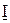на сопротивлении 
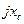. Ток 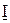отстает от напряжения U на угол 
.
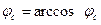Угол отставания тока от напряжения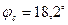 
Угол нагрузки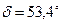
Итак, векторы в виде комплексных чисел будут равны:
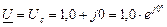
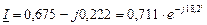
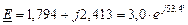
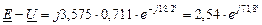
где: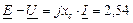 
. Здесь учтено, что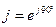 
Векторная диаграмма изображена (в масштабе) на рисунке 5.
На векторной диаграмме изображен также вектор напряжения на выходе генератора:
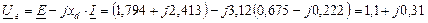
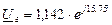
Угол между напряжением генератора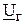 
и током 
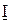определяет собой угол 
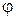нагрузки генератора
|
|
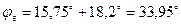
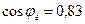оказывается близким к номинальному 0,85.
Напряжение генератора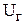 
в вольтах:
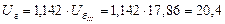кВ.
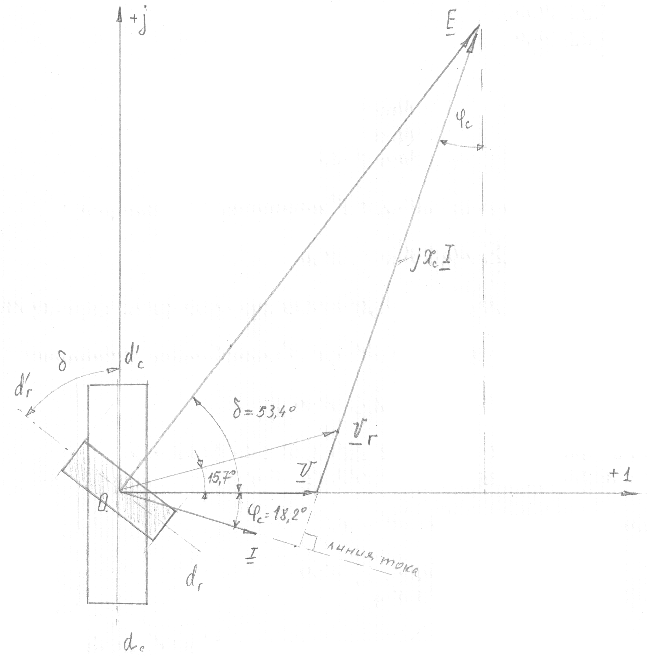
Рисунок 5
Угловое смещение осей роторов: системы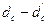 
и генератора 
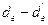на угол 
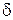определяет смещение фазовое векторов ЭДС Е и напряжения приемной системы U на тот же угол .
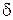Определим мощность, отдаваемую генератором (для контроля правильности расчетов):
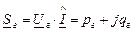
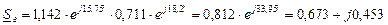
Видим, что активная мощность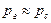 
, реактивная же мощность 
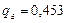частично теряется на реактивностях линии: 
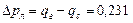, а остальная поступает в приемную систему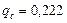 
Полученные данные говорят об осуществимости режима, при условии, что внутренняя ЭДС Е генератора будет иметь рассчитанное значение_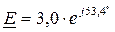 
.
16. Характеристика мощности строится в соответствии с формулой:
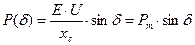
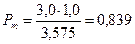
Точка “ а ” совместной работы турбины и генератора имеет координаты:
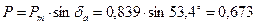
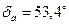
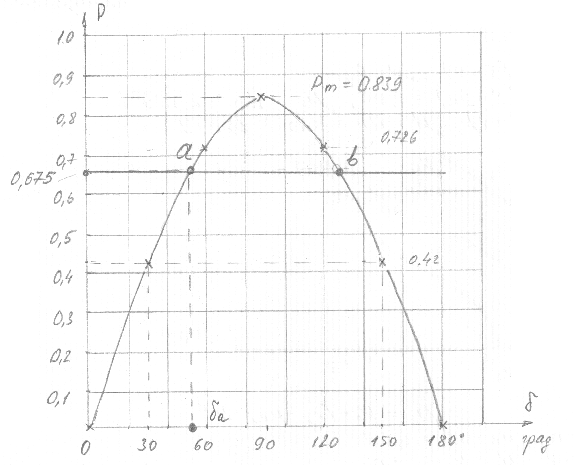
Рисунок 6.
Предел мощности передачи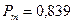 
о.е.
В мегаваттах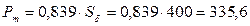 
МВт.
Фактическая нагрузка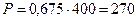 
МВт.
Запас устойчивости:
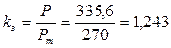
т.е. 24,3 % (норма 15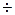 
20 %).
Точка “ а ” – точка устойчивой работы, точка “ в ” – точка неустойчивой работы.