Методы решения систем n линейных уравнений с n неизвестными
Что необходимо знать для решения систем n линейных уравнений с n неизвестными?
Для решения систем n линейных уравнений с n неизвестными необходимо знать:
- основные действия над матрицами;
- методы нахождения определителя матрицы;
- метод нахождения обратной матрицы;
- методы решения систем n линейных уравнений с n неизвестными.
Как отличить линейное уравнение от нелинейного?
В линейном уравнении, в отличие от нелинейного, все переменные находятся в первой степени, и график зависимости переменных представляет собой прямую линию.
Методы решения систем n линейных уравнений с n неизвестными. Метод Крамера
Рассмотрим систему n линейных уравнений с n неизвестными:
 , где:
, где:
- x1, x2, …, xn – неизвестные;
- aij (где  ;
;  ) – коэффициенты при неизвестных, константы, ϵ R;
) – коэффициенты при неизвестных, константы, ϵ R;
- b1, b2, …, bn – свободные члены, ϵ R.
Из данных, имеющихся в системе уравнений, мы можем составить две матрицы:
1)  – матрица системы (уравнений). В эту матрицу вошли константы, находящиеся перед неизвестными в системе уравнений;
– матрица системы (уравнений). В эту матрицу вошли константы, находящиеся перед неизвестными в системе уравнений;
2) 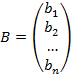 – эта матрица представляет собой столбец свободных членов из правой части системы уравнений.
– эта матрица представляет собой столбец свободных членов из правой части системы уравнений.
Теперь самое время перейти непосредственно к теореме (правилу) Крамера: если определитель матрицы системы (матрицы A) отличен от нуля, то система имеет решение и притом только одно. Данное решение определяется следующей формулой:
 , где:
, где:
- Δ – определитель матрицы системы (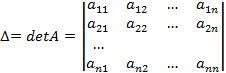 );
);
- Δk – определитель матрицы, полученный из матрицы системы заменой k-го столбца столбцом свободных членов (единственным столбцом матрицы B);
- xk – решение системы при данном Δk (где  ).
).
Так,  ,
,  ,
, 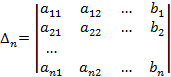 .
.
Следует отметить два важных обстоятельства:
1) если определитель матрицы системы равен нулю ( ), а среди определителей Δk есть отличные от нуля, тогда система не имеет решений;
), а среди определителей Δk есть отличные от нуля, тогда система не имеет решений;
2) если  (где
(где  ), а среди миноров (n-1)-го порядка определителя Δ есть отличные от нуля, тогда система сводится к (n-1) уравнению и имеет множество решений.
), а среди миноров (n-1)-го порядка определителя Δ есть отличные от нуля, тогда система сводится к (n-1) уравнению и имеет множество решений.
В качестве примера рассмотрим следующую систему уравнений:
 .
.
Для того чтобы решить данную систему уравнений, необходимо сначала сделать некоторые преобразования. На первом этапе преобразований перенесём все неизвестные в левую часть системы уравнений, а свободные члены – в правую:
 .
.
На втором этапе преобразований поменяем местами неизвестные так, чтобы они стояли в порядке возрастания их индексов:
 .
.
Теперь, когда все элементы системы уравнений находятся на своих местах, можно приступить к её решению. Записываем матрицу системы и матрицу свободных членов:
1)  ;
;
2)  .
.
Далее находим определитель матрицы системы:
 .
.
 , следовательно, можем сделать вывод, что система имеет решение. Теперь найдём определители Δk (где
, следовательно, можем сделать вывод, что система имеет решение. Теперь найдём определители Δk (где 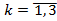 ):
):
 ;
;
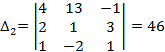 ;
;
 .
.
Мы нашли всё, что необходимо для получения решений системы. Остаётся лишь подставить полученные значения определителей в уравнение  и найти значения неизвестных:
и найти значения неизвестных:
 ;
;
 ;
;
 .
.
Ответ:  ,
, 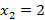 ,
,  .
.
Методы решения систем n линейных уравнений с n неизвестными. Матричные уравнения
Матричные уравнения – это уравнения следующих видов:  и
и  .
.
Рассмотрим сначала уравнение вида  . Здесь A, X и B – матрицы, удовлетворяющие следующим условиям:
. Здесь A, X и B – матрицы, удовлетворяющие следующим условиям:
1) A – квадратная невырожденная матрица размерности  . Невырожденная – значит такая, что для неё существует обратная матрица (
. Невырожденная – значит такая, что для неё существует обратная матрица (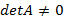 );
);
2) X – прямоугольная матрица размерности  . Размерность матрицы X должна быть такой (
. Размерность матрицы X должна быть такой ( ), чтобы на неё можно было умножить матрицу A (
), чтобы на неё можно было умножить матрицу A ( );
);
3) B – прямоугольная матрица размерности  . Размерность матрицы B (
. Размерность матрицы B ( ) получается в результате умножения матрицы A (
) получается в результате умножения матрицы A ( ) на матрицу X (
) на матрицу X ( ) и не может быть другой.
) и не может быть другой.
Пусть A и B – известные матрицы, X – неизвестная матрица. Чтобы получить матрицу X из уравнения  , необходимо помножить обе части уравнения на A-1 (обратную матрицу для матрицы A). Причём сделать это нужно слева, так как с левой стороны матрица A «свободна» от произведения:
, необходимо помножить обе части уравнения на A-1 (обратную матрицу для матрицы A). Причём сделать это нужно слева, так как с левой стороны матрица A «свободна» от произведения:
 .
.
Произведение  даёт нам единичную матрицу E, поэтому можем записать:
даёт нам единичную матрицу E, поэтому можем записать:
 .
.
Так как умножение данной матрицы на единичную и наоборот (единичной на данную) представляет собой саму данную матрицу, то  , и тогда:
, и тогда:
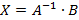 .
.
В случае матричного уравнения  (где A – квадратная невырожденная матрица размерности
(где A – квадратная невырожденная матрица размерности  ; X – прямоугольная матрица размерности
; X – прямоугольная матрица размерности 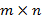 ; B – прямоугольная матрица размерности
; B – прямоугольная матрица размерности 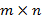 ) помножать обе части уравнения на A-1 следует справа (справа матрица A «свободна»):
) помножать обе части уравнения на A-1 следует справа (справа матрица A «свободна»):
 .
.
Далее вспоминаем, что 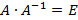 , а
, а  :
:
 и, наконец,
и, наконец,  .
.
Теперь рассмотрим применение матричных уравнений для решения систем n линейных уравнений с n неизвестными. Возьмём уже знакомую нам систему уравнений из первого примера:
 .
.
Преобразуем её к удобному для решения виду:
 .
.
Далее запишем матрицу системы (A), матрицу свободных членов (B) и матрицу неизвестных (X):
1)  ;
;
2)  ;
;
3)  .
.
Матричное уравнение будет выглядеть следующим образом:
 .
.
Получим X в явном виде:
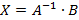 .
.
Теперь найдём обратную матрицу для матрицы A:
 .
.
Так как определитель матрицы A отличен от нуля ( ), то матрица A – невырожденная, и A-1 существует. Для того чтобы найти A-1, необходимо получить алгебраические дополнения Aij. Для этого воспользуемся формулой
), то матрица A – невырожденная, и A-1 существует. Для того чтобы найти A-1, необходимо получить алгебраические дополнения Aij. Для этого воспользуемся формулой  , где Mij – минор (определитель, полученный из матрицы A одновременным вычёркиванием i-ой строки и j-го столбца):
, где Mij – минор (определитель, полученный из матрицы A одновременным вычёркиванием i-ой строки и j-го столбца):
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
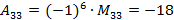 .
.
Теперь можем записать саму обратную матрицу для матрицы A:
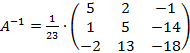 .
.
Матричное уравнение будет выглядеть следующим образом:
 .
.
Перемножим матрицы A-1 и B:
 .
.
Ответ:  ,
, 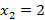 ,
,  .
.