В общем виде существует три модели оценки ценных бумаг:
1) Фундаменталистская модель
2) Технократическая модель
3) «Ходьба наугад»
Фундаменталистская модель предполагает, что каждая ценная бумага имеет внутреннюю ценность, которая количественно может быть рассчитана посредством дисконтирования будущих доходов от этой ценной бумаги.
Технократы полагают, что для определения текущей стоимости любой ценной бумаги нужно проанализировать динамику цены этой бумаги за прошедшие три, пять лет и вывести среднюю величину.
Последователи теории «ходьбы наугад» утверждали, что будущую цену ценной бумаги могут определить только эксперты, исходя из опыта работы на рынке ценных бумаг.
Наиболее распространенной является первая теория, согласно которой рыночная стоимость ценной бумаги рассчитывается по формуле:
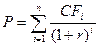
Модели оценки облигаций
Облигации имеют нарицательную (номинальную), выкупную, рыночную цену.
Выкупная цена – цена, по которой эмитент выкупает облигацию по истечению срока займа, данная цена определяется условиями займа.
Рыночная цена – цена, которая определяется коньюктурой рынка.
Значение рыночной цены облигации в процентах к номиналу называется курсом облигации.
Периодическая выплата процентов по облигациям осуществляется по купонам, т.е. отрезным талонам с напечатанной на нем купонной ставкой. Факт оплаты купона сопровождается изъятием его из прилагаемой к облигации карты.
По способам выплаты дохода различают:
- облигации с фиксированной купонной ставкой;
- облигации с плавающей купонной ставкой;
- облигации с равномерно возрастающей купонной ставкой.
Способы оценки основных видов облигаций выражаются в определении их текущей рыночной цены.
|
|
1) Оценка облигаций с нулевым купоном
Для данного вида облигаций характерна разовая выплата при окончании срока займа.
Текущая рыночная цена этих облигаций определяется по формуле:
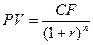
где:
CF – сумма, выплачиваемая при погашении облигации;
n – число лет займа.
Пример: Облигации с нулевым купоном нарицательной стоимостью 100 000 рублей, сроком погашения 5 лет продаются за 63 012 рублей. Проанализировать целесообразность их приобретения, если имеется возможность альтернативного инвестирования с нормой дохода 12%.
Решение:
Из формулы 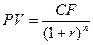выражаем r.
, подставляем значения
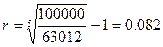, или 8,2%.
Таким образом, наиболее эффективный вариант – вложить денежные средства в альтернативный проект.
2) Оценка бессрочных облигаций
Бессрочная облигация предусматривает неопределенно долгую выплату дохода в установленном размере денежного дохода CF.
При этом процентная ставка r может быть фиксированной и плавающей.
В первом случае текущая рыночная цена данного вида облигаций определяется по формуле:
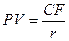
Во втором случае текущая рыночная цена бессрочной облигации определяется для каждого значения r по соответствующему периоду.
Пример: Рассчитать текущую рыночную цену бессрочной облигации, если выплачиваемый по ней годовой доход составляет 10000 рублей, рыночная приемлемая норма дохода 18%.
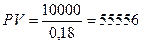руб.
3) Оценка облигаций с постоянным доходом
Денежный поток по данному виду облигаций складывается из двух частей:
- одинаковые по годам поступления (С);
- поступления в конце периода займа, равные выкупной стоимости, чаще всего нарицательной (F).
|
|
Текущая рыночная цена облигации с постоянным доходом рассчитывается по формуле:
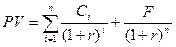
Пример: Оценить текущую стоимость облигации с нарицательной стоимостью 100 000 рублей, купонной ставкой 15% годовых и сроком погашения через 4 года, рыночная норма дохода 10%.
Ежегодный денежный поток в данном случае составит:
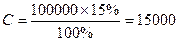рублей.
При этом в последнем периоде помимо 15000 рублей инвестору причитается нарицательная стоимость облигации:
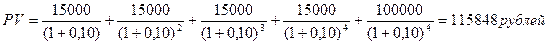
Исходя из расчетов, можно сделать выводы:
- если рыночная норма дохода больше фиксированной купонной ставки, то облигация продается по цене ниже номинала;
- если рыночная норма дохода меньше фиксированной купонной ставки, то облигация продается по цене выше номинала;
- если рыночная норма дохода совпадает с фиксированной купонной ставкой, то облигация продается по нарицательной стоимости.
Рыночная норма дохода и текущая цена облигации с фиксированной купонной ставкой находятся в обратной пропорциональной зависимости.
В случае если информация о рыночной норме дохода не известна, ее можно вывести из формулы оценки облигаций с постоянным доходом:
Пример: Рассчитать норму дохода облигации нарицательной стоимостью 100 000 рублей с годовой купонной ставкой 9%, имеющей текущую рыночную цену 84000 рублей. Облигация будет приниматься к погашению через 8 лет.
Определяем купонный доход по облигации:
С = 100 000*9% = 9 000 рублей
Модели оценки акций
Оценка акций с равномерно возрастающими дивидендами
Если базовая величина дивиденда (С) ежегодно увеличивается на на величину q, то цена данной акции будет рассчитываться по формуле:
|
|
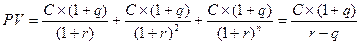- модель Городона
Пример: имеется акция, дивиденд по которой, будут увеличиваться на 10% в год. Дивиденд по акции два доллара, минимально необходимая норма дохода 16%, рассчитать рыночную цену акции.
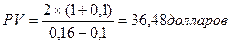
Оценка акций с изменяющимся темпом прироста
Если величина прироста дивиденда изменяется по периодам, то рыночная стоимость акции рассчитывается по каждому подинтервалу.
Например, если выделить два подинтервала с темпами прироста q и p, тогда рыночная цена акции составит:
ИНВЕСТИЦИОННЫЙ РИСК
1) Фактор риска в инвестиционных операциях
Золотое правило инвестирования: доход от вложений всегда прямо пропорционален риску нп который готов пойти инвестор ради желаемого результата.
Размер прогнозируемого дохода зависит от многих обстоятельств важнейшим из которыя является сама вероятность выигрыша, т.е. вероятность успеха выступает характеристикой рискованности операций, а обратная отдача на вложения капитала есть своего рада плата за риск. С учетом этого цена риска укрупнено может быть рассчитана по формуле:
Цена риска = (доход по рисковым ЦБ – доход по безрисковым ЦБ) / среднее отклонение дохода по рисковым ЦБ от безрисковых
Отсюда следую два важных вывода:
1. для эффективного ведения инвестиционной деятельности необходим капитал достаточный для осуществления диверсификации вложений в противном случае ведение операций на фондовом рынке лучше поручить специализированным компаниям, способных аккумулировать средства многих инвесторов.
2. степень риска конкретной ценной бумаги целесообразно определять по отношению к другим ЦБ, а лучше всего по отношению к степени риска фондового рынка в целом.
2) Риск и доход для индивидуального инвестора
Для количественной оценки риска используются следующие показатели:
- средняя ожидаемая норма дохода;
- вариация;
- стандартная дивиация;
- коэффициент вариации.
Ср. ожидаемая норма дохода.
Имеется 10000 долл., которые необходимо инвестировать на 1 год, при этом реально существуют 4 варианта:
1. годичные векселя казначейства США по которым предлагается *% дохода, через год векселя будут выкуплены, что гарантировано государством.
2. облигации корпорации с 9% доходом и сроком погашения 10 лет, однако фирма продаст облигации через год и норма дахода будет зависеть от от ставки %, которая сложится на конец года.
3. проект предполагающий нулевые поступления в течении года, а выплаты в конце года будут зависеть от состояния экономики.
4. проект 2, который отличается от проекта 1 поступлениями в течении года.
Применительно к экономическим задачам использование теории вероятностисводится к определению вероятности наступления событий и к выбору из возможных вариаетов самого предпочтительного, т.е. выбирается вариант исходя из наибольшей величины матожидания.
Матожидание любого события равно абсолютной величине события умноженного на вероятность его наступления.
Вероятность наступления события может быть определена субъективными или объективными методами.
Объективный основан на анализе имеющейся информации (реализации аналогичных проектов). Субъективный основан на суждениях экспертов.
Для расчета показателей рисков необходимо в первую очередь норму предполагаемого дохода по каждому из 4 вариантов.
Оценка предполагаемого дохода
| состояние экономики | вероятность ситуации | векселя | облигации | проект 1 | проект 2 |
| глубокий спад | 0,05 | ||||
| небольшой спад | 0,2 | ||||
| средний рост | 0,5 | ||||
| небольшой подъем | 0,2 | 8,5 | |||
| мощный подъем | 0,05 | ||||
| 9,2 | 10,3 |
Средняя ожидаемая норма дохода рассчитывается по формуле:
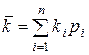
где:
ki – ожидаемый доход по данному проекту при i-ом состоянии экономики;
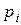- вероятность получения ожидаемого дохода при i-ом состоянии экономики ki;
Для количественной оценки риска необходимо рассчитать вариацию:
где:
ki – ожидаемая норма дохода по данному проекту при i-ом состоянии экономики, %.
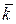- средняя ожидаемая норма дохода по данному проекту, %;
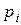- вероятность получения ожидаемого дохода при i-ом состоянии экономики.
1. Поскольку вариация измеряется в тех же единицах, что и ожидаемых доход, но возведенных в квадрат для инвестора представляется затруднительным ее использование при аналитической оценке альтернативных вариантов. В этой связи используется показатель стандартная девиация, которая определяется по формуле:
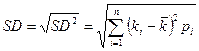
Стандартная девиация указывает на сколько процентов в среднем может отличаться ожидаемая норма дохода от средней величины дохода с учетом рисков.
В той связи, что стандартная девиация характеризует абсолютную величину рисков, представляется сложным сравнение проектов с различными ожидаемыми доходами, поэтому используется относительный показатель – коэффициент вариации (СV), который рассчитывается по формуле:
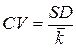
Коэффициент характеризует величину риска, приходящегося на единицу среднего дохода.
Рассчитанные показатели сведем в таблицу
| показатель | векселя | облигации | проект 1 | проект 2 |
| средняя ожидаемая норма дохода | 9,2 | 10,3 | ||
| вариация | 0,71 | 19,31 | 23,1 | |
| стандартная дивиация | 0,84 | 4,39 | 4,82 | |
| коэффициент вариации | 0,09 | 0,43 | 0,4 |
Выбор проекта для инвестирования будет зависеть от того, какой показатель мы возьмем за основу оценки риска.
По ожидаемой норме дохода предпочтителен проект 2.
Когда необходимо использовать несколько критериев риска, то обычно используется так называемый средне вариационный критерий, который основывается на 2 предположениях:
1. стремление максимально избежать риска
2. распределение, которое оценивается при принятии решения.
1-ое означает, что если существуют два варианта с одинаковыми доходами, то выбирается вариант с наименьшим показателем риска.
Средневариационный критерий предполагает сравнение ожидаемых доходов и вариации.
Хотя средневариационный критерий является полезным при принятии инвестиционного решения, им нужно пользоваться осторожно, т.к. норма распределения часто может нарушаться. Мы же его принимаем как предпосылку.
Исходя из рассмотренного можно сделать следующие выводы:
- исходя из нормы дохода предпочтителен 1 вариант
- исходя из критериев риска вариации – проект 1, коэффициента вариации – проект 2.
- исходя из стремления избежать риска – более предпочтителен 1 вариант (векселя)
3) вторая сторона проблемы изучения риска не по отдельным инвестициям, а по портфелю, при обосновании портфеляимеется возможность снижения риска путем диверсификации.
Ожидаемая норма дохода по портфельным инвестициям представляет собой средневзвешенную величину ожидаемых доходов, по каждым отдельным инвестициям, входящим в этот портфель.
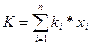
Где х – доля i-ой группы инвестиций в портфеле.
Полученный результат необходимо проанализировать с т.з. рыночного риска, поскольку комбинация различных групп инвестиций является сложной, многокомпонентным сочетанием. Для анализа рыночного риска используют комплексные расчеты.
Стандартная дивиация не является не является отдельной средневзвешенной отдельных проектов.
Это связано с тем, что проекты определенным образом соотносятся друг с другом. Теоретически всегда имеется возможность такитм образом сгруппировать портфель, что стандартная дивиация будет равна 0, т.е. инвестиционные проекты обладая риском, сгруппированы в портфель перестают быть рискованными. Между тем это возможно в том случае, если вид корелляции между ними таков, что они находятся в противофазе.
Если коэффициент корреляции=1, то проекты не связаны и снижение риска невозможно.
На практике большинство проектов имеют положительный коэффициент корреляции от +0,5 до + 0,6.
Риск для портфеля инвестиций измеряется стандартной дивиацией распределения доходов по формуле:
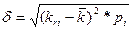
Для анализа портфеля инвестирования вводится понятие ковариация, которое имеет 2 основные характеристики:
- вариация доходов по акциям
- тенденция этих доходов увеличиваться или уменьшаться в одно и тоже время при движении доходов по другим группам акций, т.е. ковариация между проектами А и Б показывает происходит ли увеличение или снижение доходов по этим проектам одновременно и на сколько велико это движение.
Т.е. можно утверждать:
- ковариация будет большой и положительной, если по группам инвестиций существует большая вариация и уровень доходов по ним меняется одновременно и в том же направлении.
- ковариация будет большой и отрицательной для 2 групп инвестиций с большой вариацией и величинами доходов, которые движутся одновременно в противоположных направлениях.
- ковариация будет незначительной, если доходы по группам инвестиций меняются несвязанным образом (независимы), однако вариация по каждой группе инвестиций низкая.