Перевод чисел из одной системы счисления в другую

Рассмотрим правила перевода чисел из одной системы счисления в другую.

Для перевода шестнадцатеричного числа в двоичную систему счисления каждый символ исходного числа заменяется соответствующим четырехразрядным двоичным числом (см. таблицу). В полученном дво­ичном числе удаляются незначащие нули (крайние слева в целой части и крайние справа — в дробной).

Пример 1. Перевести число 7D2,E₁₆ из шестнадцатеричной системы счисления в двоичную.

Решение:

7 D 2, E = 011111010010,1110

â â â â

0111 1101 0010, 1110

Ответ: 7D2,E₁₆ = 11111010010,111₂

Для перевода двоичного числа в шестнадцатеричную систему счисления поступают следующим образом: двигаясь от десятичной запятой сначала влево, затем вправо, разбивают двоичное число на группы по четыре разряда, дополняя, при необходимости, нулями крайние левую и правую группы. Затем каждую группу из четырех разрядов заменяют соответствующим шестнадцатеричным символом (см. таблицу).

Пример 2. Перевести число 10111110001,001₂ из двоичной системы счисления в шестнадцатеричную.

Решение:

0101 1111 0001, 0010 = 5F1,2

â â â â

5 F 1, 2

Ответ: 10111110001,001₂ = 5F1,2₁₆

Для перевода двоичного или шестнадцатеричного числа в десятичную систему счисления достаточно представить число в виде полинома (*), подставив в него известные коэффициенты, и вычислить сумму.

Решение:

11011,11 = 1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 1*2° + 1*2¹ +1*2² = = 16+8+0+2+1+0,5+0,25 = 27,75

Ответ: 11011,112 = 27,7510

Пример 4. Перевести число 4A,1₁₆ из шестнадцатеричной системы счисления в десятичную.

Решение:

4А,1 = 4*16¹ + 10*16° + 1*16^-1 = 64+10+0062,5 = 74,0625

Ответ: 4А,1₁₆ = 74,0625₁₀

Например, В9h = 11*16+9 = 185; 4А9Fh = 4*16³ + 10*16² +9*16 +15 = 19103.

Для перевода целого десятичного числа в двоичную систему счисления необходимо делить это число, а затем получаемые частные на 2 до тех пор, пока ча­стное не станет равным 1. Последнее частное и ос­татки записывают в порядке, обратном их получению.

Пример 5. Перевести число 25₁₀ из десятичной системы счисления в двоичную.

Решение:

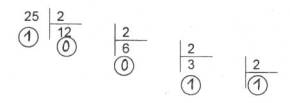
Ответ: 25₁₀ = 11001₂

Для перевода целого десятичного числа в шестнадцатеричную систему счисления необходимо делить это число, а затем получаемые частные на 16 до тех пор, пока частное не станет меньше 16. Последнее частное и остатки записывают в порядке, обратном их получению.

Пример 6. Перевести число 177₁₀ из десятичной системы счисления в шестнадцатеричную.

Решение:

Ответ: 177₁₀ = В1₁₆

Для перевода правильной десятичной дроби (целая часть равна 0) в двоичную систему счисления необходимо умножать исходную дробь и дробные части получающихся произведений на 2. Операцию умножения повторяют до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута заданная точность (определенное количество символов). Целые части получающихся произведений дают последовательность цифр, которая является записью полученного двоичного числа.

Пример 7. Перевести правильную десятичную дробь 0,1875₁₀ в двоичную систему счисления.

Ответ: 0,1875₁₀ = 0,0011₂

Для перевода правильной десятичной дроби в шестнадцатеричную систему счисления необходимо умножать исходную дробь и дробные части получающихся произведений на 16. Операцию умножения повторяют до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута заданная точность. Целые части получающихся произведений дают последовательность цифр, которая является записью полученного шестнадцатеричного числа.

Пример 8. Перевести правильную десятичную дробь 0,47₁₀ из десятичной системы счисления в шестнадцатеричную с точностью до пяти знаков.

Решение.

Ответ: 0,47₁₀ = 0,7851Е₁₆

При переводе неправильной десятичной дроби в двоичную и шестнадцатеричную системы счисления отдельно переводят целую и дробную части, руководствуясь соответствующими правилами.

Пример 9. Перевести число 9,625 из десятичной системы счисления в двоичную.

Решение:

Переведем целую часть десятичного числа в двоичную систему счисления (см. пример 5):

9₁₀ = 1001₂

Затем переведем правильную дробь (см. пример 7):

0,625₁₀ = 0,101₂

Ответ: 9,625₁₀ = 1001,101₂

Пример 10. Перевести число 399,125 из десятичной системы счисления в шестнадцатеричную.

Решение:

Переведем целую часть десятичного числа в шестнадцатеричную систему счисления (см. пример 6):

399₁₀ = 18F₁₆

Затем переведем правильную дробь (см. пример 8):

0,125₁₀=0,2₁₆

Ответ: 399,125₁₀ = 18F,2₁₆

При переводе чисел из десятичной системы счисления в шестнадцатеричную и наоборот иногда применяют так называемый «двойной перевод», когда в качестве промежуточного используют двоичное число. Перевод осуществляют по схеме 10 ® 2®16 или 16®2®10.

Пример 11. Перевести число 741,625₁₀ из десятич­ной системы счисления в шестнадцатеричную.

Решение:

Переведем десятичное число в двоичную систему счисления (см. пример 9):

741,625₁₀ = 1011100101,101₂

Затем переведем полученное двоичное число в шестнадцатеричную систему счисления (см. пример 2): 1011100101,101₂ = 2Е5,А₁₆

Ответ: 741,625₁₀ = 2E5,A₁₆

Пример 12. Перевести число DC,2₁₆ из шестнадцатеричной системы счисления в десятичную.

Решение:

Переведем шестнадцатеричное число в двоичную систему счисления (см. пример 1):

DC,2₁₆= 11011100,0012

Затем полученное двоичное число переведем в десятичную систему счисления (см. пример 3):

11011100,001₂ = 200,125₁₀

Ответ: DC,2₁₆ = 200,125₁₀