30-31
Динамика материальной точки (м.т.)определяется двумя законами Ньютона: ƩFi=R=ma
ƩFi – сумма сил действующая на м.т. со стороны какого либо объекта. Выполняется принцип супер позиции сил => Сумма сил считается одной силой – равнодействующей. R является функцией от координаты точки в системе отчета, скорости и времени.
Дифференциальные уравнения движения материальной точки:  , в проекции на декартовы оси коорд.:
, в проекции на декартовы оси коорд.:  , на оси естественного трехгранника:
, на оси естественного трехгранника:  ;
;  ;
;  (
( – проекция ускорения на бинормаль), т.е.
– проекция ускорения на бинормаль), т.е.  (
( – радиус кривизны траектории в текущей точке). В случае плоского движения точки в полярных координатах:
– радиус кривизны траектории в текущей точке). В случае плоского движения точки в полярных координатах:  .
.
Две основные задачи динамики для свободной точки:
При решении этих задач исходными являются дифференциальные уравнения движения точки, записанные в общем виде в декартовых или естественных координатах.
Первая задача динамики (обратная)– зная закон движения точки, определить действующую на нее силу;
Вторая задача динамики (основная) (прямая) – зная действующие на точку силы, определить закон движения точки.
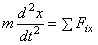 – дифференциальное ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее решение
– дифференциальное ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее решение  .
.
Постоянные интегрирования C 1, C 2 ищут из начальных условий: t =0, x = x 0,  =Vx=V0, x=f(t,x 0, V 0) – частное решение – закон движения точки.
=Vx=V0, x=f(t,x 0, V 0) – частное решение – закон движения точки.
Решаются обе эти задачи с помощью уравнений, выражающих основной закон динамики, так как эти уравнения связывают ускорение  т.е. величину, характеризующую движение точки, и действующие на нее силы.
т.е. величину, характеризующую движение точки, и действующие на нее силы.
Несвободной материальной точкой называется точка, свобода движения которой ограничена.
Тела, ограничивающие свободу движения точки, называются связями.
Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, которое называется уравнением связи.
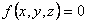
Если точка вынуждена двигаться по некоторой линии, то уравнениями связи являются уравнения этой лини.
 ,
, 
Таким образом, движение несвободной материальной точки зависит не только от приложенных к ней активных сил и начальных условий, но так же от имеющихся связей. При этом значения начальных параметров должны удовлетворять уравнениям связей.
Связи бывают двухсторонние или удерживающие и односторонние или неудерживающие.
Связь называется двухсторонней если, накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве на которых должна находится точка.
математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:
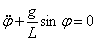 , где L – длина нити. Если
, где L – длина нити. Если  , то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс. T=2π√(L/g)
, то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс. T=2π√(L/g)
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид.
Гармоническими являются колебания,которые происходят под действием силы,пропорциональной смещению колеблящейся точки и направленной противоположно этому смещению.

или

Затухающие колебания(в среде с сопротивлением) при действии 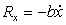 сила сопротивления, пропорциональная скорости (вязкое трение).
сила сопротивления, пропорциональная скорости (вязкое трение).  , обозначив
, обозначив  , получаем:
, получаем:
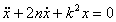
характеристическое уравнение: 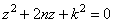 , (z тоже что и x). его корни:
, (z тоже что и x). его корни: 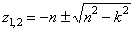 . а) При n<k корни мнимые, отсюда общее решение дифф.ур-ия имеет вид:
. а) При n<k корни мнимые, отсюда общее решение дифф.ур-ия имеет вид: 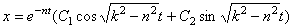 , обозначив
, обозначив  ,
, 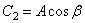 имеем
имеем  . Множитель
. Множитель  показывает, что колебания затухающие. График заключен между двумя симметричными относительно оси t кривыми
показывает, что колебания затухающие. График заключен между двумя симметричными относительно оси t кривыми  . Из начальных условий:
. Из начальных условий:  ,
, 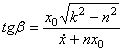 ; частота затухающих колебаний:
; частота затухающих колебаний:  ; период:
; период: 
32.
основной закон динамики поступательного движения - Второй закон НьютонаF=dp/dt, p=m*v
если материальная точка находится в состоянии относительного покоя, геометрическая сумма действующих на нее сил и переносной силы инерции равна нулю. Следует отметить, что выполнения условия не означает, что после сообщения точке начальной скорости она будет двигаться равномерно и прямолинейно относительно подвижной системы, как это имеет место в инерциальной системе отсчета.
Сила инерции материальной точки представляет собой противодействие материальной точки изменению ее скорости и приложена к телу, сообщающему этой точке ускорение. Сила инерции равна по модулю произведению массы материальной точки на модуль ее ускорения и направлена в сторону, противоположную ускорению  . При неравномерном криволинейном движении точки силу инерции, представленной в виде касательной (
. При неравномерном криволинейном движении точки силу инерции, представленной в виде касательной (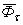 ), и нормальной (
), и нормальной ( ) силами инерции. Эти силы направлены противоположно касательному и нормальному ускорению
) силами инерции. Эти силы направлены противоположно касательному и нормальному ускорению  ,
, 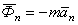 ,
,  ,
,  . В случае равномерного движения точки по кривой
. В случае равномерного движения точки по кривой 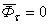 . В случае равномерного движения точки по прямой
. В случае равномерного движения точки по прямой  . Если точка принадлежит твердому телу, вращающемуся вокруг неподвижной оси, то модуль ее вращательной и центробежной сил инерции определяется по формулам:
. Если точка принадлежит твердому телу, вращающемуся вокруг неподвижной оси, то модуль ее вращательной и центробежной сил инерции определяется по формулам:  ,
,  , где
, где  ,
,  — угловое ускорение и угловая скорость тела.
— угловое ускорение и угловая скорость тела.
Принцип Даламбера (метод кинетостатики)
В каждый момент движения сумма активных сил, реакций связей и сил инерции равна нулю  — принцип Даламбера для материальной точки.
— принцип Даламбера для материальной точки.
 – внешняя сила,
– внешняя сила,  – внутренняя сила. Сила инерции:
– внутренняя сила. Сила инерции:  , знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.
, знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.
Для системы добавляется уравнение моментов: 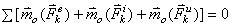 .
.
Обозначают:  – главный вектор сил инерции,
– главный вектор сил инерции,  – главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю
– главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю  ,
,  , получаем:
, получаем:  ,
, 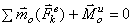 — уравнения кинетостатики. Принцип Даламбера для системы – если в любой момент времени к каждой точке системы приложить, кроме реально действующих сил, соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять уравнения статики. Это упрощает процесс решения задач.
— уравнения кинетостатики. Принцип Даламбера для системы – если в любой момент времени к каждой точке системы приложить, кроме реально действующих сил, соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять уравнения статики. Это упрощает процесс решения задач.
Главный вектор сил инерции  равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
Главный момент сил инерции зависит от вида движения: при поступательном движении 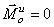 ; при плоском
; при плоском  , при вращении вокруг оси z, проходящей через центр масс тела,
, при вращении вокруг оси z, проходящей через центр масс тела, 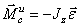 .
.
Механическая система – совокупность взаимосвязанных между собой тел или материальных точек. Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
Центр масс (центр инерции) – геометрическая точка, радиус-вектор  которой определяется равенством:
которой определяется равенством: 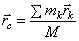 , где
, где  – радиусы-векторы точек, образующих систему. Координаты центра масс:
– радиусы-векторы точек, образующих систему. Координаты центра масс:  и т.д.
и т.д.
Материальная система – совокупность материальных точек, движение которых взаимосвязаны. Масса системы = сумме масс всех точек (или тел), образующих систему:  .
.
Момент инерции тела (системы) относительно оси Оz:  . При непрерывном распределении масс (тело) сумма переходит в интеграл:
. При непрерывном распределении масс (тело) сумма переходит в интеграл:  ,
, 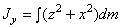 ,
, 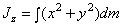 – относительно координатных осей.
– относительно координатных осей.  , где
, где  – радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0.
– радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0.
Теорема Гюйгенса-Штейнера момент инерции тела относительно произвольной оси равен моменту инерции относительно оси ей параллельной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями:
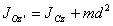 . Наименьший момент инерции будет относительно той оси, которая проходит через центр масс.
. Наименьший момент инерции будет относительно той оси, которая проходит через центр масс.

| Материальная точка массы m | На расстоянии r от точки, неподвижная | 
|

| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | 
|

| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | 
|

| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | 
|

| Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | 
|
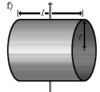
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | 
|

| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | 
|

| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | 
|

| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | 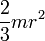
|
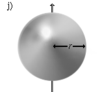
| Шар радиуса r и массы m | Ось проходит через центр шара | 
|
Билет 34
1. Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
2. Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему
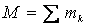 .
.
В однородном поле тяжести, для которого  , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:
, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:
 ,
, 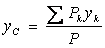 ,
, 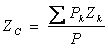 . (1)
. (1)
В полученные равенства входят только массы 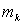 материальных точек (частиц), образующих тело, и координаты
материальных точек (частиц), образующих тело, и координаты  этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под
этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под 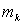 ,
,  понимать соответственно массы и координаты точек этой системы.
понимать соответственно массы и координаты точек этой системы.
Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.
Положение центра масс определяется его радиус-вектором 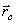
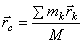 ,
,
где 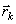 - радиус-векторы точек, образующих систему.
- радиус-векторы точек, образующих систему.
3. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая отего движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении.
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси,  .
.
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина 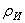 , определяемая равенством
, определяемая равенством
 ,
,
где М - масса тела.
4. Теорема Гюйгенса.
Моменты инерции данного тела относительно разных осей будут разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведенной в теле, найти момент инерции относительно любой другой оси, ей параллельной.
5. 
6. Рис.35
Проведем через центр масс С тела произвольные оси Cx'y'z', а через любую точку О на оси Сх' - оси Oxyz, такие, что Оy ½½ Сy', Oz ½½ Cz' (рис. 35). Расстояние между осями Cz' и Оz обозначим через d. Тогда

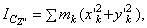
но, как видно из рисунка, для любой точки тела  или
или  , а
, а  . Подставляя эти значения
. Подставляя эти значения  , в выражение для
, в выражение для  и вынося общие множители d 2 и 2d за скобки, получим
и вынося общие множители d 2 и 2d за скобки, получим

В правой части равенства первая сумма равна Icz', а вторая - массе тела М. Найдем значение третьей суммы. На основании формул для координат центра масс  .Так как в нашем случае точка С является началом координат, то x C = 0 и, следовательно,
.Так как в нашем случае точка С является началом координат, то x C = 0 и, следовательно, 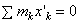 . Окончательно получаем:
. Окончательно получаем:
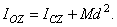
Формула выражает следующую теорему Гюйгенса:
Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.
Билет 35
1. Принцип Даламбера.
Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой  . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил 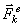 и
и  (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение  .
.
Введем в рассмотрение величину
 ,
,
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции).
Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам 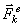 и
и  прибавить силу инерции
прибавить силу инерции  , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет
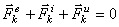 .
.
Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает  . Перенося здесь член
. Перенося здесь член  в правую часть равенства и придем к последнему соотношению.
в правую часть равенства и придем к последнему соотношению.
Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.
Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.
Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы 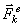 и
и  , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями
, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями  . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:

Введём обозначения:


Величины 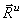 и
и  представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
 ,
,  (1)
(1)
Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил.
В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.