Согласно теореме Пуансо, доказанной в статике твердого тела, система сил инерции твердого тела приводится к одной силе или главному вектору, приложенному в центре приведения, и одной паре сил, момент которой равен главному моменту сил инерции относительно центра приведения. Причем величина и направление главного вектора не зависят от выбора центра приведения (главный вектор является инвариантом системы сил), а величина и направление главного момента изменяются при смене центра приведения. 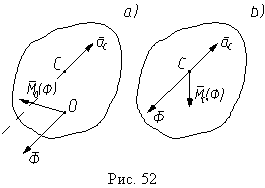
По следствию принципа Даламбера (6) центром приведения является центр O (подвижный или неподвижный), поэтому главный вектор сил инерции твердого тела приложен в этом центре, а его величина и направление определяется по формуле (8) и не зависят от выбора центра приведения. Главный момент MO(Фi) сил инерции твердого тела также приложен в центре приведения, но зависит от выбора центра приведения. На рис. 52, a показан результат приведения сил инерции твердого тела, когда за центр приведения выбран центр O, а на рис 52, b показан тот же результат, но когда за центр приведения выбран центр масс тела C. Главный вектор сил инерции не изменил ни направления, ни величины, сменилась только точка его приложения, но зато изменился главный момент сил инерции и MO(Фi) <> MO(Фi). То есть главный вектор сил инерции совсем не обязательно проходит через центр масс тела, хотя по величине он всегда равен произведению массы тела на абсолютное ускорение центра масс и направлен противоположно этому ускорению.
3. ДУ поступательного и вращательного движения 
4. ДУ плоского движения 
5. Определение динам реакций подшипника 
Билет 36
Общие теоремы динамики.

2.Центр масс механической системы и твердого тела
В билете 34 пунк 2 об этом все написано.
3.Теорема о движении центра масс мех сис-мы
Рассмотрим движущуюся систему мат. точек М1, М2, Мi, Mn, находящихся под действием внешних и внутренних сил (рис). Положение центра масс системы С определяется равенством
rc = ∑miri/m. Уравнения движения точек этой системы имеют вид
mi d2ri/dt2 = PiE + PiJ; (i = 1, 2, …, n), суммируем эти уравнения:
∑mi d2ri/dt2 =∑ PiE + ∑ PiJ (а). Преобразуем левую часть равенства, учитывая (rc = ∑miri/m) получаем: ∑mi d2ri/dt2 = d2/dt2 * ∑mi ri = d2/dt2 * (mrc) = md2rc/dt2. Геометрическая сумма внутренних сил равна 0. Уравнение (а) приобретает вид: md2rc/dt2 = ∑PiE = RE или
maC = ∑ PiE = RE (в). т.е. произведение массы системы на ускорение её центра масс = геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил. Уравнение (в) выражает теорему о движении центра масс системы, которая формулируется следующим образом: Центр масс мех. сис. движется как мат. точ. массой, равной массе всей системы, к которой приложены все внешние силы действующие на систему.
Проецируя на оси x, y, z – mxC = ∑ XiE = XE
Следствия не нашелL
Билет 37
1.Динамические меры движения материальной точки, твердого тела, механической системы
Механической системы