Из предыдущей лекции видно, что изучение движения механической системы не может основываться на детальном интегрировании ее дифференциальных уравнений движения. Такая задача слишком сложна и может быть реализована на практике только в исключительных случаях. Однако в той же лекции мы видели, что можно найти такие величины, общие для всей механической системы, изменение которых во времени позволяет сделать важные выводы о движении системы в целом. Одной из таких величин является центр масс системы. Этим же свойством обладают количество движения, кинетический момент и кинетическая энергия механической системы, называемые основными динамическими величинами механической системы.
Пусть 
— скорости точек движущиеся механической системы. Произведение массы материальной точки 
на ее вектор скорости 
называется количеством движения (импульсом) материальной точки. Для совокупности векторов количеств движения точек системы 
(рис. 27) можно определить главный вектор и главный момент.
Главный вектор количеств движения точек механической системы
называется количеством движения механической системы.
Главный момент количеств движения точек механической системы относительно некоторого центра О
называется кинетическим моментом механической системы.
2.Работа и мощность силы
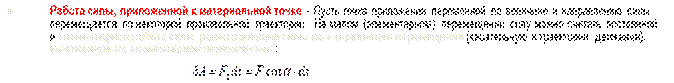
2.1.Работа и мощность пары сил
Работа пары сил с постоянным моментом MZ = const
,
Мощность пары сил (момента)
3.Аналитическое выражение элементарной работы силы
Найдем аналитическое выражение элементарной работы. Для этого разложим силу 
на составляющие 
, 
, 
по направлениям координатных осей (рис.17; сама сила на чертеже не показана).
Рис.17
Элементарное перемещение 
слагается из перемещений 
, 
, 
вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы на перемещении 
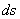можно вычислить как сумму работ её составляющих , , на перемещениях , , .
Но на перемещении совершает работу только составляющая , причем её работа равна 
. Работа на перемещениях и вычисляется аналогично. Окончательно находим: 
.
Формула дает аналитическое выражение элементарной работы силы.
Работа силы на любом конечном перемещении М 0 М 1 вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:
или
.
4.Работа и мощность силы, приложенной к вращающемуся телу
38)
КОЛИЧЕСТВО ДВИЖЕНИЯ — мера механического движения, равная для материальной точки произведению ее массы m на скорость v. Количество движения mv величина векторная, направленная так же, как скорость точки. Количество движения называется также импульсом.
И́мпульсси́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.
Теорема импульсов (в дифференциальной форме). Дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Теорема импульсов (в интегральной форме). Изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за этот же промежуток времени.
Твердое тело, имеющее одну неподвижную точку, из одного положения в любое другое можно перевести одним поворотом вокруг некоторой оси, проходящей через неподвижную точку (теорема Эйлера-Даламбера). Эту ось называют осью конечного вращения.
Кинетический момент относительно центра и оси: Производная по времени от кинетического момента механической системы относительно любой оси, проходящей через центр масс системы, в ее относительном движении по отношению к центру масс равна главному моменту внешних сил, действующих на точки системы, относительно этой оси. Если главный вектор внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно.
Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы так же, как они не изменяют ее количество движения.
39)
Отсюда следует, что кинетическую энергию точки можно рассматривать как работу, которую может произвести движущаяся точка. Кинетическая энергия поступательно движущегося тела определяется той же формулой, что и кинетическая энергия точки.
E-E0=A илиmv2/2- mv20/2=A
Теоре́маКёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс.
Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.
40)
Силовым полем называется область, в каждой точку которой, на помещённую в неё материальную точку действует сила однозначно определённая по величине и направлению в любой момент времени. Силовое поле называется не стационарным, если поле зависит явно от времени; и стационарным, если не зависит от времени t явно.
Силовое поле называется потенциальным или консервативным, если для него существует функция координат: 
такая, что проекции действующей силы могут быть вычислены через ее частные производные:
Эта функция называется потенциальной энергией.
При движении под действием потенциальных сил сумма кинетической и потенциальной энергии системы в каждом ее положении остается величиной постоянной. Это закон сохранения механической энергии.
43)
Период колеба́ний — наименьший промежуток времени, за который система совершающеем колебания совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором он находился в первоначальный момент, выбранный произвольно