Различные определения вероятности
Классическое определение вероятности
Определение 18. Если в задачеинтересует появление любого из определенных элементарных событий 
, 
, …, 
, то будем говорить, что интересует наступление события А, состоящего в выпадении одного из m элементарных исходов , , …, . Исходы , , …, будем называть исходами,благоприятными появлению события 
.
Пример 5. Опыт: брошена симметричная игральная кость. Событию – «выпало число очков, большее 3-х» – благоприятен любой из трех элементарных исходов: 
– «выпало 4 очка», 
– «выпало 5 очков», 
– «выпало 6 очков».
Определение 19 (классическое определение вероятности). Вероятностью события называют отношение числа 
элементарных исходов, благоприятных появлению события к числу 
всех равновозможных несовместных элементарных исходов, образующих полную группу:
. (23.1)
Замечание. Первый недостаток классического определения вероятности проявляется в том, что оно рассматривает конечную полную группу попарно несовместных равновозможных событий. Второй его недостаток состоит в том, что формула (23.1) пригодна тогда и только тогда, когда опыт сводится к классической схеме испытаний. Поэтому появились модификации классического определения вероятности на случай бесконечной полной группы попарно несовместных равновозможных событий и на случай неклассической схемы испытаний.
Геометрическое определение вероятности
Пусть на плоскости имеется некоторая область 
, и в ней содержится другая область 
с измеримой границей. В область наудачу бросается точка. Рассматривается событие , заключающееся в том, что точка, брошенная наудачу в область , попадет в область . Термин «брошенная наудачу » означает, что точка может попасть в любое место области , вероятность попадания в какую-либо часть области пропорциональна мере этой части (длине, площади и т.д.) и не зависит от ее расположения и формы.
|
|
Определение 20 (геометрическое определение вероятности). Геометрической вероятностью события (попадания в область ) при бросании наудачу точки в область называют величину
, (23.2)
в которой 
– мера (длина, площадь и т.д) области , 
– мера (длина, площадь и т.д.) области .
Замечание. Недостаток формулы (23.2) заключается в том, что для бесконечного числа исходов нельзя дать объективного, не зависящего от способа расчета величин и , определения вероятности.
Относительная частота события. Статистическая вероятность
Если опыт не сводится к классической схеме испытаний, то приближенное значение вероятности случайного события можно найти экспериментально.
Определение 21. Если проведена серия из опытов, в каждом из которых могло появиться или не появиться некоторое событие , то относительной частотой события в данной серии опытов называют отношение числа опытов, в которых появилось событие , к общему числу произведенных опытов:
. (23.3)
Замечание. При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Однако при увеличении числа опытов частота стабилизируется, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Этот факт называют свойством устойчивости частот. Его математическая формулировка (и доказательство) принадлежит Я. Бернулли: при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте. На основании этого свойства относительную частоту события при достаточно большом числе опытов можно принять за приближенное значение вероятности этого события. Последнее называют статистической вероятностью события .
|
|
Определение 22. Говорят, что величина 
сходится по вероятности к величине 
, если при сколь угодно малом 
вероятность неравенства 
при увеличении неограниченно приближается к единице:
.
Замечание. Применяя этот термин, можно сказать, что при увеличении числа опытов относительная частота события сходится по вероятности к вероятности события.
Алгоритм решения задач
1) Исследовать пространство элементарных исходов. Выяснить, каким оно является: конечным или бесконечным, классическим или неклассическим. Определить общее число всех элементарных исходов .
2) Определить число исходов , благоприятных появлению события .
3) Вычислить вероятность события .
Пример 6. Брошена симметричная игральная кость. Какова вероятность выпадения четного числа очков?
Решение. Обозначим событие – «выпало четное число очков».
1) Пространство элементарных событий в опыте бросания симметричной игральной кости состоит из шести попарно несовместных равновозможных элементарных исходов и может быть записано следующим образом: 
. Общее число всех равновозможных элементарных исходов 
.
|
|
2) Благоприятными событию являются исходы 
. Следовательно, число исходов, благоприятных событию , 
.
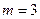3) По формуле (23.1) вероятность события : 
.
Пример 7. Набирая номер телефона, абонент забыл одну последнюю цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим событие – «набрана нужная цифра».
1) Абонент мог набрать любую из 10 цифр. Поэтому общее число возможных элементарных исходов 10. Эти исходы равновозможные (цифра набрана наудачу) и образуют полную группу (хотя бы одна цифра обязательно будет набрана), то есть 
.
2) Нужная цифра всего одна. Поэтому для события благоприятен всего один исход: 
.
3) По формуле (23.1) вероятность события : 
.
Пример 8. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что они различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение. Обозначим событие – «набраны две нужные цифры».
1) Всего можно набрать столько пар различных цифр, сколько может быть составлено размещений из 10 цифр по 2, то есть 
. Все варианты набора равновозможны (абонент набирает их наудачу) и образуют полную группу (хотя бы одна пара цифр будет набрана). Поэтому общее число равновозможных элементарных исходов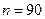 
.
2) Нужное сочетание двух цифр всего одно. Поэтому для события благоприятен всего один исход: .
3) По формуле (23.1) вероятность события : 
.
Пример 9. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей, ровно 4 стандартных.
Решение. Пусть событие – «среди 6 взятых деталей ровно 4 стандартных».
1) Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, то есть числу сочетаний из 10 элементов по 6 (
). Все исходы равновозможны (детали извлекают наудачу) и образуют полную группу (6 деталей обязательно извлечено).
2) Подсчитаем число исходов, благоприятных событию : 4 стандартные детали можно взять из 7 стандартных деталей 
способами. При этом остальные 6 – 4 = 2 детали должны быть нестандартными. Их можно взять из 10 – 7 = 3 нестандартных деталей 
способами. Следовательно, число благоприятных исходов 
.
3) По формуле (23.1) вероятность события :
.
Пример 10. Коэффициенты 
и 
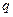квадратного уравнения 
выбираются наудачу в промежутке 
. Чему равна вероятность того, что корни будут действительными числами?
Решение. Пусть событие – «данное квадратное уравнение имеет действительные корни».
1) Так как коэффициенты и 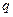квадратного уравнения выбираются наудачу в промежутке , то все исходы равновозможны, а общее число исходов бесконечно. В прямоугольных декартовых координатах множество всевозможных пар чисел и 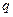задается точками единичного квадрата в I четверти (множество , рис. 23.1). Следовательно, 
.
2) Чтобы корни квадратного уравнения были действительными числами, необходимо и достаточно выполнение неравенства 
или 
. Точки, благоприятствующие событию , лежат под параболой 
(множество заштриховано, рис. 23.1). Следовательно, 
.
3) По формуле (23.2) искомая вероятность равна 
.
Пример 11. Стрелок произвел по мишени 30 выстрелов, из которых попал 25 раз. Найти относительную частоту попаданий.
Решение. Пусть событие – «стрелок попал в мишень».
1) 30 выстрелов представляют собой серию из 
опытов, в каждом из которых могло появиться или не появиться событие .
2) В данной серии опытов событие появилось в 
случаях.
3) По формуле (23.3) относительная частота события равна 
.