1. В ящике 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: 1) белый, 2) черный, 3) синий, 4) красный, 5) белый или черный, 6) синий или красный, 7) белый, черный или синий.
2. В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых шаров и 4 черных. Из каждого ящика вынули по одному шару. Какова вероятность того, что оба шара белые?
3. В условиях предыдущей задачи определить вероятность того, что один из вынутых шаров белый, а другой – черный.
4. В ящике 6 белых и 8 черных шаров. Из ящика последовательно вынули 2 шара (не возвращая первый вынутый шар в ящик). Найти вероятность того, что оба шара белые.
5. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.
6. В условиях предыдущей задачи определить вероятность того, что в цель попадет хотя бы один стрелок.
7. Вероятность выхода станка из строя в течение одного рабочего дня равна a (a – малое положительное число, второй степенью которого можно пренебречь). Какова вероятность того, что за 5 дней станок ни разу не выйдет из строя? Решить задачу при a=0,01.
8. В ящике a белых и b черных шаров. Какова вероятность того, что из двух вынутых шаров один белый, а другой – черный? Вынутый шар в ящик не возвращается.
9. В ящике 20 белых и 10 черных шаров. Вынули подряд 4 шара, причем каждый вынутый шар возвращают в ящик перед извлечением следующего и шары в ящике перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется 2 белых?
10. Вероятность появления события А равна 0,4. Какова вероятность того, что при 10 испытаниях событие А появится не более трех раз?
|
|
11. Определить вероятность того, что в семье, имеющей 5 детей, будет 3 девочки и 2 мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
12. В условиях предыдущей задачи найти вероятность того, что среди детей будет не больше 3-х девочек.
13. В ящике 10 белых и 40 черных шаров. Вынимают подряд 14 шаров, причем цвет вынутого шара регистрируют, а затем шар возвращают в ящик. Определить наивероятнейшее число появлений белого шара.
14. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель.
15. В результате многолетних наблюдений установлено, что вероятность выпадения дождя 1 октября в данном городе равна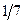 
. Определить наивероятнейшее число дождливых дней 1 октября в данном городе за 40 лет.
16. Имеется 4 ящика. В первом ящике 1 белый и 1 черный шар, во втором – 2 белых и 3 черных шара, в третьем – 3 белых и 5 черных шаров, в четвертом – 4 белых и 7 черных шаров. Событие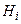 
– выбор i- го ящика (i =1,2,3,4). Известно, что вероятность выбора i- го ящика равна 
. Выбирают наугад один из ящиков и вынимают из него шар. Найти вероятность того, что этот шар белый.
17. Имеются 3 одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 черных шаров, в третьем – 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Найти вероятность того, что шар вынут из первого ящика.
18. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
|
|
19. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
20. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если они извлекаются: а) без возвращения; б) с возвращением (извлеченный кубик возвращается в мешочек).
21. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
22. Стрелку для поражения мишени предложено 5 винтовок, причем 3 из них – с оптическим прицелом. Вероятность поражения мишени из винтовки с оптическим прицелом – 0,9; из обычной – 0,55. Найти вероятность того, что мишень будет поражена, если стрелку для одного выстрела предложена наугад взятая винтовка.
23. Для участия в студенческих отборочных соревнованиях выделено из 1-й группы 4 студента, из 2-й – 6, из 3-й – 5. Вероятности того, что отобранный студент из 1, 2 или 3-й группы попадет в сборную, равны соответственно 0,5; 0,4; 0,3. Наудачу выбранный участник соревнований попал в сборную. К какой из трех групп он вероятнее всего принадлежит?
24. Найти вероятность того, что среди взятых наудачу 5 деталей – 2 стандартные, если вероятность того, что каждая деталь стандартна, равна 0,9.