Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
 .
.
Обобщение теоремы на случай произвольного конечного числа попарно несовместных событий:  .
.
Пример 1. В ящике 30 шаров: 10 красных, 5 синих и 15 белых. Вынули один шар. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного, либо синего шара. Пусть событие  – появление красного шара, а событие
– появление красного шара, а событие  – появление синего шара. Тогда событие
– появление синего шара. Тогда событие  +
+  – появление цветного шара. Вероятность события
– появление цветного шара. Вероятность события  :
: 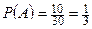 . Вероятность события
. Вероятность события  :
:  . Появление шара одного цвета исключает появление шара другого цвета, поэтому события А и
. Появление шара одного цвета исключает появление шара другого цвета, поэтому события А и  несовместны. По теореме о сложении вероятностей несовместных событий
несовместны. По теореме о сложении вероятностей несовместных событий  .
.
Определение 1. Событие  называют независимым от события
называют независимым от события  , если вероятность события
, если вероятность события  не зависит от того, произошло событие
не зависит от того, произошло событие  или нет.
или нет.
Определение 2. Событие  называют зависимым от события
называют зависимым от события  , если вероятность события
, если вероятность события  меняется в зависимости от того, произошло событие
меняется в зависимости от того, произошло событие  или нет.
или нет.
Определение 3. Вероятность события  , вычисленную при условии, что имело место другое событие
, вычисленную при условии, что имело место другое событие  , называют условной вероятностью события А и обозначают
, называют условной вероятностью события А и обозначают  .
.
Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
 , если события
, если события  и
и  зависимы;
зависимы;
 , если события
, если события  и
и  независимы.
независимы.
Обобщение теоремы на случай произвольного конечного числа независимых событий:  .
.
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 2. В ящике находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в ящик. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный и при третьем – синий.
Решение. Пусть событие  – при первом испытании появится белый шар, событие
– при первом испытании появится белый шар, событие  – при втором испытании появится черный шар; событие
– при втором испытании появится черный шар; событие  – при третьем испытании появится синий шар. Вероятность появления белого шара при первом испытании
– при третьем испытании появится синий шар. Вероятность появления белого шара при первом испытании  . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, то есть условная вероятность
. Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, то есть условная вероятность  . Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором черный, равна
. Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором черный, равна  . Так как события
. Так как события  ,
,  и
и  совместны, то искомая вероятность
совместны, то искомая вероятность
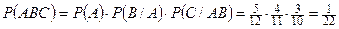 .
.
Пример 3. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна 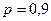 . Стрелок произвел три выстрела. Найти вероятность того, что он попал три раза.
. Стрелок произвел три выстрела. Найти вероятность того, что он попал три раза.
Решение. Пусть событие  – стрелок попал в мишень при первом выстреле, событие
– стрелок попал в мишень при первом выстреле, событие  – стрелок попал в мишень при втором выстреле; событие
– стрелок попал в мишень при втором выстреле; событие  – стрелок попал в мишень при третьем выстреле. Вероятности этих событий по условию равны между собой:
– стрелок попал в мишень при третьем выстреле. Вероятности этих событий по условию равны между собой: 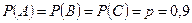 . Так как вероятность попадания в цель при каждом из выстрелов не зависит от результата остальных выстрелов, то все три события независимы, то
. Так как вероятность попадания в цель при каждом из выстрелов не зависит от результата остальных выстрелов, то все три события независимы, то  .
.
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
 .
.
Пример 4. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны:  ,
,  . Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.
. Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.
Решение. Пусть событие  – попадание в цель первого орудия, событие В – попадание в цель второго орудия. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. Вероятность события АВ (оба орудия попали в цель) равна
– попадание в цель первого орудия, событие В – попадание в цель второго орудия. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. Вероятность события АВ (оба орудия попали в цель) равна  . Так как события А и В совместны, то искомая вероятность
. Так как события А и В совместны, то искомая вероятность 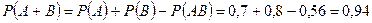 .
.
Теорема о вероятности появления хотя бы одного из совокупности независимых событий. Вероятность появления хотя бы одного из независимых событий А 1, А 2, …, Аn равна разности между единицей и произведением вероятностей противоположных событий  ,
, 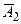 , …,
, …,  :
: 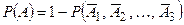 .
.
Пример 5. Вероятности попадания в цель при стрельбе из трех орудий соответственно равны:  ,
,  ,
, 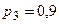 . Найти вероятность попадания хотя бы одним из орудий при одном залпе из всех орудий.
. Найти вероятность попадания хотя бы одним из орудий при одном залпе из всех орудий.
Решение. Пусть событие  – попадание в цель хотя бы одним из орудий при одном залпе из всех орудий, событие А 1 – попадание в цель первым орудием, А 2 – попадание в цель вторым орудием, А 3 – попадание в цель третьим орудием. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому события А 1, А 2, А 3 независимы. Вероятности событий, противоположных событиям А 1, А 2, А 3 (то есть вероятности промахов), соответственно равны:
– попадание в цель хотя бы одним из орудий при одном залпе из всех орудий, событие А 1 – попадание в цель первым орудием, А 2 – попадание в цель вторым орудием, А 3 – попадание в цель третьим орудием. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому события А 1, А 2, А 3 независимы. Вероятности событий, противоположных событиям А 1, А 2, А 3 (то есть вероятности промахов), соответственно равны:
 ;
;
 ;
;
 .
.
Тогда искомая вероятность  .
.
Теорема о полной вероятности. Пусть событие  может произойти вместе с одним из событий
может произойти вместе с одним из событий  ,
,  , …,
, …,  (гипотез), образующих полную группу попарно несовместных событий. Тогда вероятность события
(гипотез), образующих полную группу попарно несовместных событий. Тогда вероятность события  можно определить по формуле
можно определить по формуле
 .
.
Пример 6. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а вероятность второго – 0,9. Найти вероятность того, что взятая наудачу деталь из выбранного наудачу набора – стандартная.
Решение. Пусть событие  – извлеченная деталь стандартна, событие
– извлеченная деталь стандартна, событие  – деталь извлечена из первого набора, событие
– деталь извлечена из первого набора, событие  – деталь извлечена из второго набора. Так как деталь вынимают из наугад выбранного набора, то события
– деталь извлечена из второго набора. Так как деталь вынимают из наугад выбранного набора, то события  и
и  равновозможные, и их вероятности
равновозможные, и их вероятности 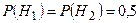 .
.
Условная вероятность того, что из первого набора будет извлечена стандартная деталь  . Условная вероятность того, что из второго набора будет извлечена стандартная деталь
. Условная вероятность того, что из второго набора будет извлечена стандартная деталь 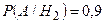 . Тогда искомая вероятность того, что взятая наудачу деталь из выбранного наудачу набора будет стандартной, по формуле полной вероятности равна
. Тогда искомая вероятность того, что взятая наудачу деталь из выбранного наудачу набора будет стандартной, по формуле полной вероятности равна
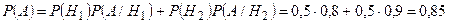 .
.
Формула Бейеса. Условная вероятность события  в предположении, что событие
в предположении, что событие  уже произошло, определяют по формуле
уже произошло, определяют по формуле
 (
( ).
).
Вероятности  , вычисленные по формуле Бейеса, называют вероятностями гипотез.
, вычисленные по формуле Бейеса, называют вероятностями гипотез.
Пример 7. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Деталь при проверке была признана стандартной. Найти вероятность того, что ее проверил первый контролер.
Решение. Обозначим через  событие, состоящее в том, что деталь признана стандартной, гипотеза
событие, состоящее в том, что деталь признана стандартной, гипотеза  – деталь проверил первый контролер, гипотеза
– деталь проверил первый контролер, гипотеза  – деталь проверил второй контролер. По условию задачи имеем
– деталь проверил второй контролер. По условию задачи имеем
 (вероятность того, что деталь попадет к первому контролеру),
(вероятность того, что деталь попадет к первому контролеру),
 (вероятность того, что деталь попадет ко второму контролеру),
(вероятность того, что деталь попадет ко второму контролеру),
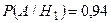 (вероятность того, что деталь будет признана стандартной первым контролером),
(вероятность того, что деталь будет признана стандартной первым контролером),
 (вероятность того, что деталь будет признана стандартной вторым контролером).
(вероятность того, что деталь будет признана стандартной вторым контролером).
Искомую вероятность того, что признанную стандартной деталь проверил первый контролер, найдем по формуле Бейеса:
 .
.
До испытания вероятность гипотезы  равнялась 0,6, а после того, как стал известен результат испытания, условная вероятность этой гипотезы изменилась и стала равной 0,59.
равнялась 0,6, а после того, как стал известен результат испытания, условная вероятность этой гипотезы изменилась и стала равной 0,59.
Схема Бернулли
В научной и практической деятельности постоянно приходится проводить многократно повторяющиеся испытания в сходных условиях (физический и технический эксперимент, метеорология, организация производства и т.д.). Как правило, при этом результаты предшествующих испытаний никак не сказываются на последующих. Простейший тип таких испытаний состоит в том, что в каждом из испытаний некоторое событие  может появиться с одной и той же вероятностью
может появиться с одной и той же вероятностью  и эта вероятность остается одной и той же, независимо от результатов предшествующих и последующих испытаний. Этот тип событий называют схемой Бернулли (по имени исследователя Якоба Бернулли). Схема Бернулли положила начало многим дальнейшим построениям и обобщениям теории вероятностей.
и эта вероятность остается одной и той же, независимо от результатов предшествующих и последующих испытаний. Этот тип событий называют схемой Бернулли (по имени исследователя Якоба Бернулли). Схема Бернулли положила начало многим дальнейшим построениям и обобщениям теории вероятностей.
Пусть проводится серия из n независимых испытаний, в каждом из которых с вероятностью  может наступить некоторое событие
может наступить некоторое событие  . В схеме Бернулли под элементарным событием принято понимать последовательность наступлений или ненаступлений события
. В схеме Бернулли под элементарным событием принято понимать последовательность наступлений или ненаступлений события  в данной последовательности испытаний.
в данной последовательности испытаний.
Формула Бернулли. Пусть производится 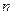 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  одна и та же и равна
одна и та же и равна  , то вероятность того, что событие
, то вероятность того, что событие  появится в этих
появится в этих 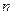 испытаниях ровно
испытаниях ровно 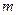 раз, вычисляют по формуле
раз, вычисляют по формуле
 .
.
Пример 8. Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы, равна  . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4-х суток не превысит нормы.
. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4-х суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на продолжении каждых из 6 суток постоянна и равна  . Тогда вероятность того, что расход электроэнергии в течение 4-х суток из 6 не превысит нормы, по формуле Бернулли, равна
. Тогда вероятность того, что расход электроэнергии в течение 4-х суток из 6 не превысит нормы, по формуле Бернулли, равна  .
.
Свойства поведения  как функции от
как функции от 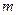
1.  .
.
2. Если  (или
(или  ), то
), то  (вероятность
(вероятность  с увеличением
с увеличением 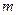 от 0 до
от 0 до  возрастает).
возрастает).
3. Если  (или
(или 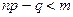 ), то
), то 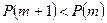 (вероятность
(вероятность  с увеличением
с увеличением 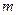 от
от  до
до 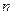 убывает).
убывает).
4. Если  (или
(или  ), то
), то  . Если
. Если  является целым числом, то максимальное значение вероятность
является целым числом, то максимальное значение вероятность  принимает для двух значений
принимает для двух значений 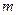 , а именно для
, а именно для  и
и  . Если
. Если  не является целым числом, то максимального значения вероятность
не является целым числом, то максимального значения вероятность  достигает при
достигает при  , равном наименьшему целому числу, большему
, равном наименьшему целому числу, большему 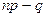 .
.
Определение 4. Число  называют наивероятнейшим числом наступлений события
называют наивероятнейшим числом наступлений события  в
в 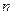 испытаниях, если значение
испытаниях, если значение  при
при  не меньше остальных значений
не меньше остальных значений  , то есть
, то есть 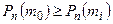 при
при  .
.
Если  и
и 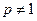 , то число
, то число  можно определить из двойного неравенства
можно определить из двойного неравенства
 .
.
Разность граничных значений в этом двойном неравенстве равна 1. Если  является целым числом, то имеется два наивероятнейших значения
является целым числом, то имеется два наивероятнейших значения 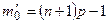 и
и 
Пример 9. Вероятность изделию некоторого производства оказаться бракованным равна 0,005. Чему равна вероятность того, что из 10 000 наудачу взятых изделий бракованных изделий окажется: а) ровно 40; б) не более 70?
Решение. 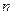 =10 000,
=10 000,  =0,005. Поэтому по формуле Бернулли находим
=0,005. Поэтому по формуле Бернулли находим
а)  ;
;
б) вероятность того, что число бракованных изделий окажется не больше 70, равна сумме вероятностей числу бракованных изделий оказаться равным 1, 2, 3, …, 70. Таким образом,
 .
.
Замечание. Пример 9 показывает, что при решении подобных задач возникают задачи, требующие приближенного вычисления сумм  для заданных
для заданных  и достаточно больших
и достаточно больших 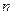 . Точно также необходимы приближенные формулы для вычисления вероятностей
. Точно также необходимы приближенные формулы для вычисления вероятностей  при больших значениях
при больших значениях 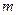 и
и 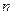 или же при малых
или же при малых 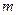 , но больших
, но больших 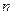 . Задача приближенного вычисления
. Задача приближенного вычисления  и
и  была решена А. Муавром.
была решена А. Муавром.