Бином Ньютона - формула.
Формула бинома Ньютона для натуральных n имеет вид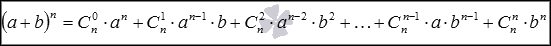 
, где 
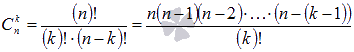- биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).
К примеру, известная формула сокращенного умножения "квадрат суммы" вида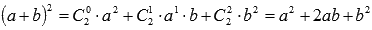 
есть частный случай бинома Ньютона при n=2.
Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)n, а выражение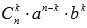 
называют (k+1) -ым членом разложения, k=0,1,2,…,n.
К началу страницы
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.
Треугольник Паскаля.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:
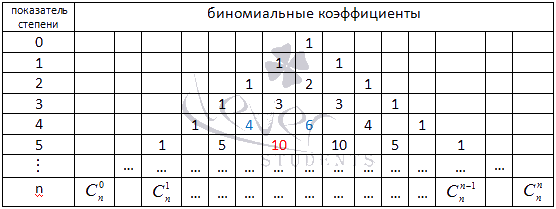
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Свойства биномиальных коэффициентов.
Для коэффициентов бинома Ньютона справедливы следующие свойства:
· коэффициенты, равноудаленные от начала и конца разложения, равны между собой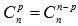 
, p=0,1,2,…,n;
· 
;
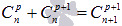· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: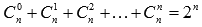 
;
· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Первые два свойства являются свойствами числа сочетаний.
К началу страницы
Доказательство формулы бинома Ньютона.
Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства 
.
Воспользуемся для доказательства методом математической индукции.
1. Проверим справедливость разложения для какого-нибудь n, допустим, для n = 3.
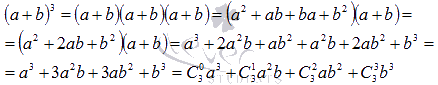
Получили верное равенство.
2. Предположим, что равенство верно для n-1, то есть, что справедливо равенство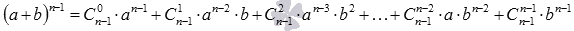 
.
3. Докажем, что верно равенство , основываясь на предположении второго пункта.
Поехали!
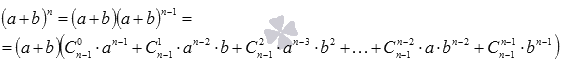
Раскрываем скобки
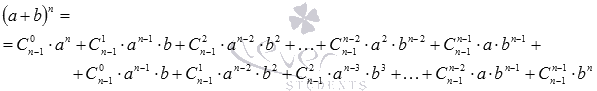
Группируем слагаемые
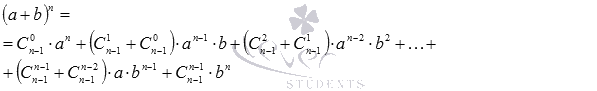
Так как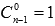 
и 
, то 
; так как 
и 
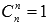, то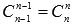 
; более того, используя свойство сочетаний 
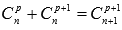, получим
Подставив эти результаты в полученное выше равенство
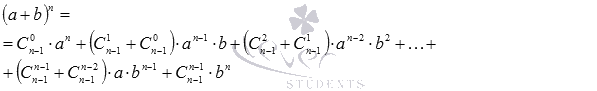
придем к формуле бинома Ньютона .
Этим доказана формула бинома Ньютона.
К началу страницы
Бином Ньютона - применение при решении примеров и задач.
Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.
Пример.
Напишите разложение выражения (a+b)5 по формуле бинома Ньютона.
Решение.
Смотрим на строку треугольника Паскаля, соответствующую пятой степени. Биномиальными коэффициентами будут числа 1, 5, 10, 10, 5, 1. Таким образом, имеем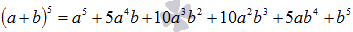 
.
Пример.
Найдите коэффициент бинома Ньютона для шестого члена разложения выражения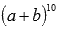 
.
Решение.
В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:
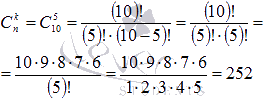
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Пример.
Доказать, что значение выражения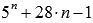 
, где n – натуральное число, делится на 16 без остатка.
Решение.
Представим первое слагаемое выражение как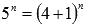 
и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16.