Механические гармонические колебания
Незатухающие гармонические колебания
1. Процесс, при котором отклонение некоторой величины от положения равновесия (смещение  ) зависит от времени
) зависит от времени  по закону синуса или косинуса
по закону синуса или косинуса
 (1)
(1)
называется гармоническим колебанием. Величина 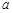 – максимальное отклонение от положения равновесия – называется амплитудой колебания, аргумент косинуса
– максимальное отклонение от положения равновесия – называется амплитудой колебания, аргумент косинуса  называется фазой,
называется фазой, 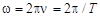 – круговая частота. Число колебаний в единицу времени
– круговая частота. Число колебаний в единицу времени 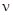 называется частотой; время
называется частотой; время  , за которое совершается одно полное колебание, называется периодом. Величина
, за которое совершается одно полное колебание, называется периодом. Величина  , определяющая величину смещения при
, определяющая величину смещения при 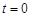 ,
, 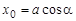 , называется начальной фазой. Зависимость
, называется начальной фазой. Зависимость 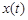 при гармоническом законе можно представить также в виде
при гармоническом законе можно представить также в виде
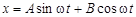 (2)
(2)
либо
 , (3)
, (3)
где символ  обозначает реальную часть от комплексного числа
обозначает реальную часть от комплексного числа 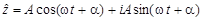 , т.е.
, т.е. 
2. Необходимым и достаточным условием возникновения гармонических колебаний является появление при отклонении тела (или системы) от равновесного положения квазиупругой возвращающей силы 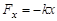 (
(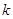 – коэффициент квазиупругой силы). Можно это условие выразить и так, зависимость потенциальной энергии
– коэффициент квазиупругой силы). Можно это условие выразить и так, зависимость потенциальной энергии  вблизи равновесного положения от смещения
вблизи равновесного положения от смещения  имеет вид
имеет вид
 .
.
С учетом приведенного выше выражения для квазиупругой силы дифференциальное уравнение движения тела запишется как
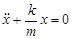 . (4)
. (4)
Общим решением этого уравнения является выражение (1), причем величины 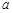 и
и  выполняют роль постоянных интегрирования, определяемых из начальных условий, а
выполняют роль постоянных интегрирования, определяемых из начальных условий, а 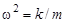 .
.
3. Типичные задачи на определение периода колебаний некоторого тела (или системы) решаются обычно одним из двух способов: а) динамический, при котором уравнение движения необходимо привести к виду (2); б) энергетический, при котором необходимо доказать, что потенциальная энергия может быть записана в виде 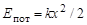 . Поскольку при гармонических колебаниях кинетическая энергия тела может быть представлена в виде
. Поскольку при гармонических колебаниях кинетическая энергия тела может быть представлена в виде
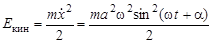 ,
,
то, приравнивая максимальную кинетическую энергию к максимальной потенциальной
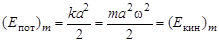 ,
,
снова приходим к формуле 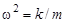 , что также в ряде задач позволяет найти частоту и период гармонических колебаний.
, что также в ряде задач позволяет найти частоту и период гармонических колебаний.
4. При незатухающих колебаниях (отсутствие трения) полная энергия колебания равна
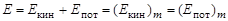

и не меняется со временем, причем  и
и  также являются периодическими функциями времени. Однако, поскольку
также являются периодическими функциями времени. Однако, поскольку
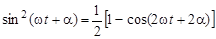 ,
,
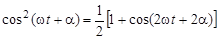 ,
,
 и
и  колеблются с частотой
колеблются с частотой 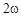 , т.е. удвоенной по сравнению с частотой смещения. В то же время
, т.е. удвоенной по сравнению с частотой смещения. В то же время
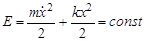 (5)
(5)
Дифференцируя по времени это соотношение, снова приходим к уравнению (4). В тех случаях, когда удается полную энергию тела представить в виде (5), это дает еще один способ нахождения частоты колебаний.
Вопросы для самоконтроля
1. В чем измеряется амплитуда гармонического колебания?
2. Что определяет фаза колебаний? Что означает утверждение: два колебания находятся в фазе, в противофазе?
3. Нарисуйте график зависимости 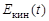 для гармонического колебания.
для гармонического колебания.
4. Как соотносятся фазы смещения, скорости и ускорения при гармоническом колебании?
5. Получите формулу для периода колебаний математического маятника.
6. Что такое приведенная длина физического маятника?
7. Какие преимущества имеются у комплексной формы записи смещения при гармонических колебаниях? (соотношение (3)).
8. Чему равны средняя кинетическая и средняя потенциальная энергии гармонического колебания?
9. Пусть смещение при гармоническом колебании дается формулой (1). Фаза скорости  имеет вид:
имеет вид:
а)  , б)
, б)  ,
,
в) 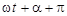 , г)
, г) 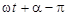 .
.
Укажите правильный ответ.
10. Пусть смещение при гармоническом колебании дается формулой (1). Фаза ускорения 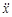 имеет вид:
имеет вид:
а)  , б)
, б)  , в)
, в) 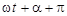 .
.
Укажите правильный ответ.
Примеры решения задач.
Пример 1. Точка совершает гармонические колебания по закону (2), где  и
и 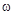 – постоянные. Найти амплитуду
– постоянные. Найти амплитуду 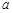 этих колебаний.
этих колебаний.
Р е ш е н и е. Чтобы найти амплитуду 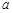 , следует привести соотношение (2) к виду (1). Для этого запишем (2) следующим образом
, следует привести соотношение (2) к виду (1). Для этого запишем (2) следующим образом
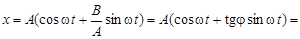
=  .
.
Здесь введено обозначение 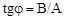 , таким образом,
, таким образом,
 .
.
Пример 2. Точка совершает гармонические колебания вдоль некоторой прямой с периодом 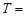 0,6 с и амплитудой
0,6 с и амплитудой 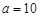 см. Найти среднюю скорость точки за время, в течение которого она проходит путь
см. Найти среднюю скорость точки за время, в течение которого она проходит путь 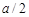 из положения равновесия.
из положения равновесия.
Р е ш е н и е. Удобно записать смещение точки в виде 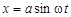 .
.
В равновесии 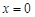 . Точка проходит путь
. Точка проходит путь 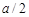 за время, определяемое соотношением
за время, определяемое соотношением
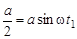 ,
,
откуда находим 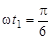 или
или 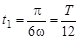 . Средняя скорость на этом участке пути равна
. Средняя скорость на этом участке пути равна
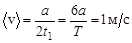 .
.
Пример 3. Частица массы  находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты
находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты  как
как  ,
,  и
и  постоянные. Найти период малых колебаний частицы около положения равновесия.
постоянные. Найти период малых колебаний частицы около положения равновесия.
Р е ш е н и е. В потенциальном поле сила, действующая на частицу, равна
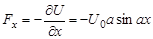 .
.
В положении равновесия  . Следовательно,
. Следовательно, 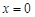 соответствует равновесному положению. При малых
соответствует равновесному положению. При малых 
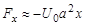 .
.
Видно, что это выражение имеет вид квазиупругой силы, причем  , а значит, частота
, а значит, частота 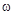 колебаний и период
колебаний и период  равны
равны
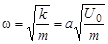 ,
,  .
.
Пример 4. Однородный стержень положили на два быстро вращающихся блока, как показано на рис. 1. Расстояние между осями блоков  , коэффициент трения между стержнем и блоками
, коэффициент трения между стержнем и блоками  . Показать, что стержень будет совершать гармонические колебания. Найти их период.
. Показать, что стержень будет совершать гармонические колебания. Найти их период.
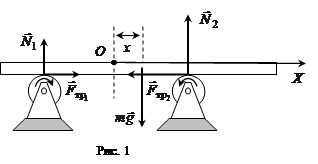
Р е ш е н и е. На рисунке показаны силы, действующие на стержень, при смещении его центра масс вправо на расстояние  . Поскольку в этом случае сила реакции
. Поскольку в этом случае сила реакции 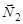 больше силы реакции
больше силы реакции 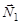 , то
, то 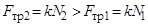 , и на стержень будет действовать возвращающая сила
, и на стержень будет действовать возвращающая сила 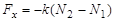 . Величины
. Величины 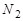 и
и 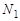 найдем из системы уравнений
найдем из системы уравнений
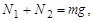
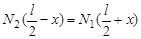 .
. 
Откуда
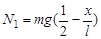 ,
, 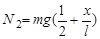 .
.
Уравнение движения стержня имеет вид

или
 .
.
Окончательно
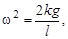
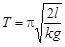 .
.
Пример 5. Тело массы  упало с высоты
упало с высоты  на чашку пружинных весов. Коэффициент жесткости пружины
на чашку пружинных весов. Коэффициент жесткости пружины  . Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний в случае, когда массы чашки и пружины можно считать малыми.
. Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний в случае, когда массы чашки и пружины можно считать малыми.
Р е ш е н и е. Прежде всего следует выбрать начало координат. Его естественно поместить в положение равновесия, относительно которого и будут происходить колебания. Под действием груза  , положенного на чашку весов без удара, пружина прогнется на величину
, положенного на чашку весов без удара, пружина прогнется на величину 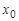 , определяемую из условия равновесия
, определяемую из условия равновесия
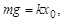
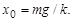
Ясно, что в момент, когда тело массы  коснется чашки весов, положение тела будет характеризоваться начальным смещением
коснется чашки весов, положение тела будет характеризоваться начальным смещением 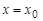 при
при 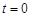 . Если пренебречь массами чашки и пружины, при их взаимодействии с упавшим телом не будет происходить перехода кинетической энергии тела в тепло (образно выражаясь, нечему нагреваться). Поэтому пружина фактически выполняет функцию некоторого эффективного потенциального поля, которое по мере сжатия пружины отбирает кинетическую энергию у груза. Начальная скорость тела (при
. Если пренебречь массами чашки и пружины, при их взаимодействии с упавшим телом не будет происходить перехода кинетической энергии тела в тепло (образно выражаясь, нечему нагреваться). Поэтому пружина фактически выполняет функцию некоторого эффективного потенциального поля, которое по мере сжатия пружины отбирает кинетическую энергию у груза. Начальная скорость тела (при 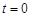 ) находится из закона сохранения энергии
) находится из закона сохранения энергии
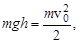
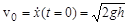
Далее можно решать задачу динамическим способом. Для чего используется уравнение движения груза в виде  или
или 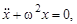
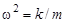 . Решение этого уравнения имеет стандартную форму (1), а амплитуда
. Решение этого уравнения имеет стандартную форму (1), а амплитуда 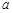 и начальная фаза
и начальная фаза  определяются из начальных условий
определяются из начальных условий 
 при
при 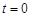 . Эти условия дают
. Эти условия дают

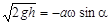 .
.
Используя основное тригонометрическое соотношение
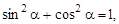
получим для амплитуды 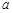 выражение
выражение

Найдем решение этой задачи также энергетическим способом. Из закона сохранения энергии следует уравнение

решение которого дает также вышеприведенный ответ для 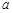 .
.
Затухающие гармонические колебания
5. Если колебание некоторого тела сопровождается трением, то энергия и амплитуда колеблющегося тела будут уменьшаться. Если сила трения зависит от скорости по закону  , то закон такого затухающего колебания будет иметь вид
, то закон такого затухающего колебания будет иметь вид
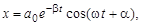 (6)
(6)
где 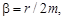
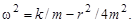
Величина 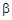 носит название коэффициента затухания, а
носит название коэффициента затухания, а  называется временем релаксации: за время
называется временем релаксации: за время 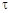 амплитуда колебаний уменьшается в
амплитуда колебаний уменьшается в 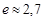 раз. Затухающие колебания характеризуют также логарифмическим коэффициентом затухания
раз. Затухающие колебания характеризуют также логарифмическим коэффициентом затухания
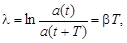
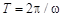 (7)
(7)
и добротностью  где
где 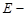 полная энергия колебаний в некоторый момент времени
полная энергия колебаний в некоторый момент времени  , а
, а  потеря энергии колебаний за отрезок времени, равный периоду колебаний
потеря энергии колебаний за отрезок времени, равный периоду колебаний  и следующий за моментом времени
и следующий за моментом времени 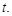 При выполнении неравенства
При выполнении неравенства  затухающие колебания невозможны и процесс становится апериодическим.
затухающие колебания невозможны и процесс становится апериодическим.
Вопросы для самоконтроля
11. Вывести дифференциальное уравнение затухающих колебаний, решением которого является закон (1).
12. Дать определение логарифмического декремента затухания.
13. Каков физический смысл добротности? Указание: принять во внимание формулы  и
и 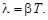

14. Изобразить графически зависимость амплитуды затухающих колебаний от времени.
15. Добротность при затухающем колебании дается формулой:
а) 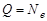 , б)
, б) 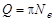 , в)
, в) 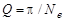 , г)
, г)  ,
,
где 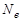 - число колебаний, за которое амплитуда затухающего колебания уменьшится в
- число колебаний, за которое амплитуда затухающего колебания уменьшится в  раз.
раз.
Укажите правильное утверждение.
Примеры решения задач
Пример 6. Амплитуда затухающих колебаний в начальный момент времени равна 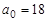 см. Через
см. Через 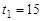 с после начала движения она равна
с после начала движения она равна  см. В какой момент времени
см. В какой момент времени  амплитуда будет равна
амплитуда будет равна 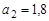 см.
см.
Р е ш е н и е. Воспользуемся зависимостью амплитуды затухающих колебаний от времени
 .
.
Отсюда
 ,
,  .
.
Из этих соотношений можно найти
 с.
с.
Пример 7. Точка совершает колебания с частотой 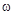 . Найти коэффициент затухания
. Найти коэффициент затухания 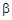 , если в начальный момент времени скорость точки равна нулю, а ее смещение из положения равновесия в
, если в начальный момент времени скорость точки равна нулю, а ее смещение из положения равновесия в 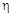 раз меньше амплитуды.
раз меньше амплитуды.
Р е ш е н и е. Найдем с помощью (6) скорость точки
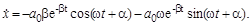
По условию задачи
0 =  (8)
(8)
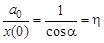 или
или 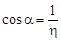 ,
, 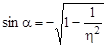 .
.
Тогда
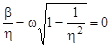 или
или 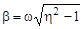 .
.
(Здесь принято 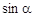 < 0, поскольку иначе правая часть уравнения (8) будет больше нуля).
< 0, поскольку иначе правая часть уравнения (8) будет больше нуля).