Метод векторных диаграмм.

6. Решение многих задач о малых колебаниях значительно упрощается и становится наглядным, если изображать гармонические колебания в виде векторов на плоскости (см. рис.2).

На плоскости проведем ось . Из точки , находящейся на оси , под углом (положительным направлением будем считать направление против часовой стрелки) к построим вектор длиной . При вращении этого вектора с угловой скоростью проекция конца вектора перемещается по оси в интервале значений от до . В соответствии с определением косинуса координата этой проекции изменяется со временем по закону

Таким образом, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой равной , круговой частотой 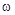, равной угловой скорости вращения вектора, и начальной фазой .

Векторное представление колебаний тесно связано также с часто используемым методом представления колебаний с помощью комплексных чисел (см. формулу (3)). Действительно, из формул Эйлера

(9)

следует, что

, (10)

 

В то же время комплексное число можно также записать в виде

, (11)

где и – полярные координаты (модуль и аргумент комплексного числа).

Соотношения между и приведены на рис.3. Если считать и 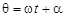, то становится очевидным, что гармонические колебания вполне однозначно определяются вектором, вращающимся в комплексной плоскости.

7. Векторное представление колебаний особенно удобно в задачах, где приходится колебания складывать. Возможны случаи, когда тело участвует одновременно в нескольких колебаниях. Если, например, шарик подвесить на пружине к потолку каюты корабля, качающегося на волнах, то движение шарика относительно суши будет складываться из колебаний корабля относительно суши и колебаний шарика относительно корабля.

Если складываемые колебания происходят с одной и той же частотой 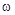, то сложив векторы, соответствующие отдельным колебаниям в начальный момент времени 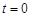, можно утверждать, что с течением времени полученная картинка сложения векторов, вращающихся с угловой скоростью против часовой стрелки, не будет деформироваться. При этом найденная результирующая амплитуда сохраняет свою величину и при времени .

Примеры решения задач

Пример 8. Решим задачу из примера 1 методом векторных диаграмм.

Р е ш е н и е. Приведем первое колебание 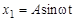к стандартному для метода векторных диаграмм виду

и сложим векторно с колебанием .

Из рисунка 4 видно, что результирующая амплитуда колебания равна 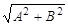, а начальная фаза 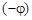определяется соотношением , что совпадает с решением, полученным в примере 1.

Пример 9. Найти амплитуду колебаний, которые возникают при сложении следующих колебаний одного направления:

, ;

, , .

Решать эту задачу можно по-разному.

Графический способ. На миллиметровой бумаге вычерчиваются графики слагаемых колебаний. Затем по точкам проводят графическое сложение смещений для различных моментов времени. Образуется график гармонической функции (советуем проверить). По клеткам миллиметровой бумаги отсчитывается амплитуда колебания.

Тот, кто силен в тригонометрии, может применить другой способ: сложить функции аналитически, воспользовавшись тригонометрическими соотношениями.

Один из способов основан на применении комплексных чисел. В данном случае предлагаем использовать метод векторных диаграмм.

Р е ш е н и е. а). Отметим сразу же, что оба вектора и (“шляпка” над означает, что это комплексная векторная величина) будут вращаться с одинаковой угловой скоростью . Следовательно, угол между и остается постоянным в любой момент времени . Изобразим вектор . При 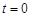он образует с осью угол . По формулам приведения . Следовательно, вектор образует с осью отрицательный угол, равный 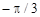(рис.5).

Сложим векторы и по правилу параллелограмма и получим (длина вектора ). Очевидно, что вектор будет вращаться также с угловой скоростью .

Проекция этого вектора на ось равна сумме проекций слагаемых векторов , следовательно, вектор представляет собой результирующее колебание. Таким образом, результирующее движение будет гармоническим колебанием с частотой и амплитудой 7,0. Амплитуда колебаний, т.е. длина вектора , может быть получена, например, при помощи теоремы ”косинусов’’.

б) Так как 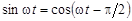, то отстает по фазе от на , а от – на (рис. 6).

В данном случае при сложении трех векторов (см. рис. 7) удобно, построив цепочку слагаемых векторов, воспользоваться правилом, по которому начало результирующего вектора совпадает с началом первого, а конец – с концом последнего из слагаемых векторов.

Из рис. 7 легко определить длину вектора . Составляющая вектора вдоль оси равна , а вдоль оси – . По теореме Пифагора:

 

Биения

8. Рассмотрим случай, когда два гармонических колебания, происходящие в одном направлении, мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называют биениями.

Обозначим частоту одного из колебаний буквой , частоту другого выразим через . Пусть << . Амплитуды обоих колебаний будем полагать одинаковыми и равными .

Пульсации амплитуды результирующего колебания легко объяснимы при рассмотрении векторных диаграмм этих колебаний. Уравнения колебаний будут иметь вид:

, (12)

(13)

На рис.8. изображено взаимное расположение векторов и и вектор результирующего колебания в некоторый момент времени . Вектор ”убежал” от на угол из-за того, что его угловая скорость превышает угловую скорость вектора на . При достижении значения, равного , и будут направлены в противоположные стороны и векторная сумма обратится в нуль.

Через ситуация повторится, амплитуда вновь обратится в ноль. Таким образом, является периодом биений, которые будут происходить с частотой , равной разности частот слагаемых колебаний.

При помощи теоремы ”косинусов” можно рассчитать длину диагонали параллелограмма (рис. 8):

Спроецируем вектор на ось и получим

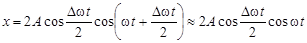. (14)

В этом выражении сомножитель изменяется значительно медленнее сомножителя Поэтому можно рассматривать приближенно как гармоническое колебание с медленно меняющейся амплитудой.

Так как амплитуда по определению неотрицательна, то будем называть амплитуду биений величину

. (15)

Пример 10. При сложении двух гармонических колебаний одного направления результирующее колебание точки имеет вид:

,

где дано в секундах. Найти круговые частоты складываемых колебаний и и период результирующего колебания.

Р е ш е н и е. Из формулы (14) следует, что:

1) , рад/с;

2) , то есть рад /с,

а так как рад/с, то рад /с.

Период биений

с.

Вынужденные колебания

9. Применим II закон Ньютона для того, чтобы написать уравнение движения груза массой , подвешенного на пружине с жесткостью в вязкой среде с коэффициентом трения , (например, в воздухе или воде) и колеблющегося под действием гармонической силы :

(16)

Разделив это уравнение на и перенеся члены с и в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:

, (17)

где , – коэффициент затухания; – собственная частота колебаний системы. Предположим, что решение (частное, т.е. не содержащее произвольных постоянных) этого уравнения имеет вид:

(18)

Вид решения подсказывает опыт. В самом деле, под действием гармонической силы через определенное время устанавливаются устойчивые колебания с постоянной амплитудой и частотой вынуждающей силы. При этом можно ожидать, что перемещение груза на пружине будет отставать от внешней силы по фазе на .

Дифференцируя (18) по времени, первые два члены уравнения (17) можно записать в следующем виде:

(19)

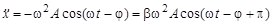(20)

Согласно уравнению (17), гармоническое колебание 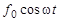является суммой трех гармонических колебаний то же частоты: (20), (19) и 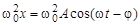. Если изобразить гармоническое колебание вектором (длиной ), направленным вправо, то вектор (19) длиной будет повернут относительно против часовой стрелки на , а (20) – на угол . Чтобы равенство (17) выполнялось, векторная сумма перечисленных векторов должна совпадать с вектором, изображающим колебание . При получающаяся векторная диаграмм изображена на рис. 9, а при – на рис.10.

В обоих случаях:

или

(21)

Из векторных диаграмм (рис. 9, 10) также получаем, что:

(22)

Окончательное решение уравнения (18) имеет вид:

. (23)

Исследование выражения (21) показывает, что амплитуда вынужденных колебаний в зависимости от частоты вынуждающей силы имеет колоколообразный график, а при 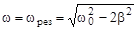достигает максимума . Это явление называется резонансом. При малых коэффициентах затухания (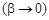 величина может достигать очень больших значений, что имеет широкое применение в технике.