Семинарское задание Кузьмина Елена СП в ИВС (игровые виды спорта)
Практическая работа к теме 3 «Оценка воспроизводимости теста»
(на примере теппинг-теста).
Тест представлял собой время 20-ти нажатий телеграфного ключа в максимально быстром темпе.
Выполняется оценка надежности теста (по ранговому коэффициенту корреляции) и расчёт необходимого числа измерений для достижения надежности r* = 0,95.
1. Заполните таблицу 1:
Таблица 1
Расчет рангового коэффициента корреляции результатов
1-й и 2-й попыток студентов СибГУФК
| № пп i | Результаты теста, с | Ранги |
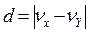
| 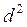
| ||
1-я попытка
(тест)
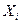 ,с ,с
| 2-я попытка
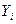 ,с ,с
| 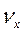
| 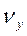
| |||
| 1,801 | 1,838 | |||||
| 1,910 | 1,854 | |||||
| 2,138 | 2,003 | |||||
| 2,181 | 2,310 | |||||
| 2,227 | 2,195 | |||||
| 2,249 | 2,398 | |||||
| 2,382 | 2,425 | |||||
| 2,416 | 2,440 | 11,5 | 3,5 | 12,25 | ||
| 2,430 | 2,720 | |||||
| 2,471 | 2,364 | 10,5 | 2,5 | 6,25 | ||
| 2,471 | 2,440 | 10,5 | 11,5 | |||
| 2,483 | 2,278 | |||||
| 2,495 | 2,538 | |||||
| 2,568 | 2,457 | |||||
| 2,584 | 2,832 | |||||
| 2,650 | 2,263 | |||||
| 2,781 | 2,810 | |||||
| 2,795 | 3,009 | |||||
| 2,946 | 3,120 | |||||
| 3,259 | 3,684 | |||||
сумма 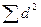 = 250,5 = 250,5
|
Определение рангов.
Ранги величин Х и Y (обозначение 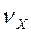 и
и 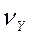 , соответственно) определяются путем ранжирования данных из граф 2 и 3. Для этого необходимо:
, соответственно) определяются путем ранжирования данных из граф 2 и 3. Для этого необходимо:
а) выписать в строчку все значения величины из соответствующейграфы в порядке возрастания (или убывания);
б) пронумеровать их;
в) для совпадающих значений рассчитать средний ранг.
Работу по ранжированию вариант X и Y удобно оформить в виде строчных табличек;
| Варианты X | |
| Номера по порядку в ранжированном ряду |  1 2 3 4 5 6 7 8 9…………. 1 2 3 4 5 6 7 8 9………….
|
Ранги 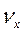
| 1 3 5 6 7 8 9………….. |
В приведенной форме фигурной скобкой выделены номера трех совпадающих вариант и показан процесс определения среднего ранга.
Для несовпадающих вариант рангиравны номерам вариант в ранжированном ряду.
Результаты ранжирования следует внести в графы4, 5 таблицы 1.
Расчет разностей рангов.
Результаты расчета
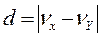
заносятся в графу 6 таблицы 1.
Знак разности не следует учитывать, т.к. в дальнейших расчетах участвуют квадраты d.
Подсчет суммы квадратов разностей рангов.
После возведения в квадрат каждого числа из графы 6 результат фиксируется в графе 7 таблицы 4. Итог суммирования данных этой графы помещается в строке «сумма».
Определение коэффициента корреляции.
Используя итог таблицы 1 рассчитать коэффициент ранговой корреляции:
· 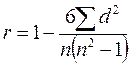 =
= 
Итоговое значение нет смысла получать точнее, чем 0,01.
Оценка уровня надежности теста
Используя вычисленное значение коэффициента 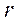 , оцените уровень надежности (воспроизводимости) избранного Вами теста.
, оцените уровень надежности (воспроизводимости) избранного Вами теста.
При этом руководствуйтесь оценочной шкалой:
0,95 и > − отличная надёжность
0,90≤0,81≤0,95 − высокая
0,80−0,90 − удовлетворительная
0,70−0,80− приемлемая
менее 0,70 − низкая
Если r < 0,7, то использовать тест для индивидуальной оценки не следует, такой тест может быть применён только для оценки группы по среднему арифметическому значению результатов испытуемых.
Результат оценки с соответствующими пояснениями отразите в отчете. Если выявленный уровень надежности окажется не достаточно высоким, то, используя формулу


где К – необходимое число попыток для расчета среднего результата каждого испытуемого.
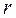 − надежность, полученная в данном эксперименте.
− надежность, полученная в данном эксперименте.
r * − желаемый уровень надежности теста (= 0,95)
Выводы по практическому заданию
В этой части отчета Вы должны в очень сжатой форме ответить навопросы:
1) является ли тест надежным и почему?
Тест представлял собой время 20-ти нажатий телеграфного ключа в максимально быстром темпе. Данный тест является надежным (высокая), потому что коэффициент ранговой корреляцииравен 0,81 (смотреть в оценочной шкале).