Определение параметров МДП-структур на основе анализа C-V характеристик

Анализ вольт-фарадных характеристик позволяет получить обширную информацию об основных параметрах МДП-структур: типе проводимости полупроводниковой подложки (n - или p -тип); концентрации легирующей примеси в подложке и законе ее распределения в приповерхностной области полупроводника; величине и знаке встроенного в диэлектрик МДП-структуры заряда; толщине подзатворного окисла; плотности поверхностных состояний на границе раздела полупроводник - диэлектрик. Рассмотрим более подробно эти вопросы.

Определение типа проводимости полупроводниковой подложки

Рис. 5 Высокочастотные ВАХ МДП-структур, изготовленных на полупроводниковых подложках n- и p-типа

Для определения типа проводимости подложки воспользуемся высокочастотной вольт-фарадной характеристикой.

Как следует из эквивалентной схемы, приведенной на рис. 1, и вида высокочастотной C-V кривой при обогащении основными носителями емкость МДП-структуры максимальна и определяется емкостью диэлектрика. В инверсии же емкость МДП-структуры максимальна. Таким образом, если максимум емкости C-V кривой лежит в более положительных напряжениях, чем минимум, то подложка изготовлена из полупроводника n -типа, если же максимум C-V кривой находится в более отрицательных напряжениях, то подложка изготовлена из полупроводника p-типа. На рис. 5 приведены для примера высокочастотные ВФХ на n - и p -типах подложки.

Определение толщины подзатворного диэлектрика

Поскольку, как было показано ранее, в обогащении емкость МДП-структуры определяется только геометрической емкостью диэлектрика C _ox, то:

(10)

где ε_ox - относительная диэлектрическая проницаемость окисла.

Отсюда следует, что:

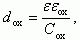(11)

Напомним, что здесь C _ox - удельная емкость подзатворного диэлектрика, т.е. емкость на единицу площади. Для подстановки в (10) экспериментальных значений необходимо сначала пронормировать емкость, т.е. разделить экспериментальное значение емкости на площадь S МДП-структуры. Как можно видеть из рис. 5, при напряжениях на затворе V _G - V _FB ≈ (2÷3) В практически для всех МДП-структур полная емкость C только на 2-3% отличается от емкости диэлектрика. Исключение составляют структуры со сверхтонким окислом d_ox < 100 A, у которых в этой области V_G становится существенным квантование в ОПЗ, и это отличие может достигать 10%.

Определение величины и профиля концентрации легирующей примеси

Для определения величины легирующей концентрации воспользуемся следующим свойством высокочастотных C-V характеристик МДП-структур: их емкость в области инверсии достигает минимальной величины C _min и определяется только емкостью области ионизованных доноров C _B и емкостью диэлектрика C _ox. При этом

(12)

Используя для емкости окисла C_ox выражение (8) и для емкости области ионизованных акцепторов, получаем:

(13)

Выражение (12 приводит к выражению для концентрации:

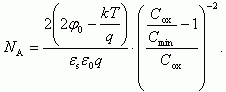(14)

На рис. 6 приведена номограмма зависимости нормированной величины емкости C _min/ C _ox от толщины d _ox для систем Si-SiO₂ с концентрацией легирующей примеси N _A в качестве параметра. Из рис. 6 видно, что чем меньше толщина диэлектрика и ниже концентрация легирующей примеси, тем больше перепад емкости от минимального до максимального значений наблюдается на ВФХ. Для определения профиля концентрации N _A от расстояния вглубь полупроводника z воспользуемся высокочастотной C-V кривой, снятой в области неравновесного обеднения. Неравновесное обеднение возможно реализовать в том случае, когда период напряжения развертки меньше постоянной τ генерационного времени неосновных носителей в ОПЗ. В этом случае величина поверхностного потенциала может быть больше ψ_s > 2φ₀, а ширина ОПЗ соответственно больше, чем ширина ОПЗ в равновесном случае. Возьмем также МДП-структуру с достаточно тонким окислом, таким, чтобы падением напряжения на окисле V _ox можно было бы пренебречь по сравнению с величиной поверхностного потенциала, т.е. V _ox << ψ_s; V _G ≈ ψ_s. В этом случае, согласно (11) и (13), тангенс угла наклона зависимости

(15)

определит величину концентрации N _A.

Значение координаты z, которой соответствует рассчитанная величина N _A, определяется при подстановке значения ψ_s = V _G в выражение для ширины ОПЗ:

Рис. 6 Зависимость нормированной величины емкости Cmin/Cox в минимуме высокочастотной ВАХ от толщины подзатворного диэлектрика dox при различных величинах концентрации легирующей примеси для кремниевых МДП-структур

(16)

В предельном случае, когда толщина окисла d _ox → 0, эту величину используют, измеряя неравновесную емкость как емкость барьеров Шоттки при обратном смещении.

Определение величины и знака встроенного заряда

Для определения величины и знака встроенного в диэлектрик МДП-структуры заряда обычно пользуются высокочастотным методом ВФХ. Для этого, зная толщину подзатворного диэлектрика d _ox, концентрацию легирующей примеси N _A и работу выхода материала затвора, рассчитывают согласно (5) теоретическое значение емкости плоских зон C _FB МДП-структуры и напряжения плоских зон V _FB = Δφ_ms.

Рис. 7 Расчет плотности поверхностных состояний дифференциальным методом: а) экспериментальная и теоретическая ВФХ для МДП-системы Si-SiO2-Al; б) зависимость сдвига напряжения ΔVG от поверхностного потенциала ψs, полученная из сечения постоянной емкости C = const МДП-структуры; в) зависимость плотности ПС от энергии E в запрещенной зоне полупроводника, полученная графическим дифференцированием кривой ΔVG(ψs) по уравнению (19)

Поскольку экспериментальная C-V кривая высокочастотная, т.е. C _ss → 0, то, проводя сечение C = const = C _FB (теор.), мы получаем при пересечении этой кривой с экспериментальной ВФХ напряжение, соответствующее ψ_s = 0, т.е. экспериментальное напряжение плоских зон V _FB (эксп.). При этом

(17)

Если Q _ox, Q _ss > 0, то V _FB (эксп.) > V _FB (теор.), и наоборот, если Q _ox, Q _ss < 0, то V _FB (эксп.) < V _FB (теор.).

Таким образом, знак и величина суммарного заряда в плоских зонах определяются соотношением (17) однозначно. Для вычленения заряда в поверхностных состояниях воспользуемся тем, что он обусловлен основными носителями (p -тип, Q _ss(ψ_s = 0) > 0 и n -тип, Q _ss(ψ_s = 0) < 0), захваченными на поверхностные состояния. Зная величину N _ss, можно рассчитать величину заряда в поверхностных состояниях Q _ss и таким образом определить величину и знак встроенного в диэлектрик заряда Q _ox.