 ,
,
в данном случае  . Так как число
. Так как число
a +bi =2 + i не является корнем характеристического уравнения, то частное решение будем искать в форме

Найдем производные  :
:


Подставим выражения  и производных в заданное уравнение, получим после приведения подобных членов
и производных в заданное уравнение, получим после приведения подобных членов

Сократим на 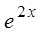 и приравняем коэффициенты при
и приравняем коэффициенты при 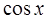 и
и 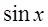 , получим два уравнения для определения А и В:
, получим два уравнения для определения А и В:
 ,
,
откуда 
 Запишем частное решение
Запишем частное решение
 .
.
Общее решение будет иметь вид

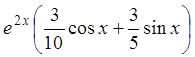 .
.
Пример 12. Найти частное решение линейного неоднородного уравнения, удовлетворяющее начальным условиям


Решение. Найдем вначале общее решение, которое будет иметь вид  . Чтобы найти общее решение соответствующего однородного уравнения
. Чтобы найти общее решение соответствующего однородного уравнения  , составим характеристическое уравнение и найдем его корни
, составим характеристическое уравнение и найдем его корни

Общее решение соответствующего однородного уравнения

Правая часть данного неоднородного уравнения имеет вид
 ,
,
в данном случае  . Так как число
. Так как число
a +bi = i не является корнем характеристического уравнения, то частное решение будем искать в форме



Подставим выражения  и производных в заданное уравнение, получим после приведения подобных членов
и производных в заданное уравнение, получим после приведения подобных членов

Приравняем коэффициенты при  и
и  , получим два уравнения для определения А и В:
, получим два уравнения для определения А и В:

Откуда  Следовательно, частным решением будет
Следовательно, частным решением будет  . Общее решение будет иметь вид
. Общее решение будет иметь вид

 .
.
Найдем С 1, С 2, используя начальные условия,
 или
или 
Отсюда С1=1, С2=0. В итоге получаем, что 
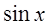 .
.
Система дифференциальных уравнений вида

где  ,
,  , …,
, …,  – неизвестные функции независимой переменной
– неизвестные функции независимой переменной  , называется нормальной системой.
, называется нормальной системой.
Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно  ,
, 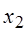 , …,
, …,  , то система дифференциальных уравнений называется линейной.
, то система дифференциальных уравнений называется линейной.
Иногда, нормальную систему дифференциальных уравнений удается свести к одному уравнению n -го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
Рассмотрим этот метод на конкретных примерах.
Пример 13. Найти общее решение системы дифференциальных уравнений

Решение. Продифференцируем по  первое уравнение:
первое уравнение:  . Подставляя сюда выражения
. Подставляя сюда выражения  и
и  из системы, получим
из системы, получим

или имеем  . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  . Следовательно, общее решение для
. Следовательно, общее решение для  запишется в виде
запишется в виде 
Общее решение y находим из первого уравнения:
 .
.
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
К КОНТРОЛЬНОЙ РАБОТЕ №6
Для решения задач 1 необходимо изучить пункт 8 программы.
Пример 14. Найти частные производные второго порядка функции 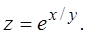
Решение. Рассматривая, переменную  как постоянную величину, получим
как постоянную величину, получим

Аналогично, рассматривая  как постоянную величину, получим
как постоянную величину, получим

Так же находим и производные второго порядка




Перед решением задачи 2 необходимо изучить пункт 9 программы.
Пример 15. Найти наибольшее и наименьшее значения функции в замкнутой области
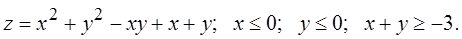
Решение. Указанная область есть треугольник АВС (рис.1).


 –1
–1 
–3 
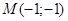
 –1
–1
–3 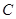
Рис. 1
Функция, дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения или в стационарной точке, или на границе области.
Найдем стационарные точки из условия  В нашем случае
В нашем случае
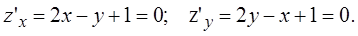
Решая систему уравнений, получим  . Точка
. Точка  является стационарной. Находим
является стационарной. Находим 
Исследуем функцию на границах. На линии  :
:  ,
,  . Задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на отрезке [–3,0].
. Задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на отрезке [–3,0].
 – стационарная точка функции одной переменной. Вычисляем
– стационарная точка функции одной переменной. Вычисляем 
На линии  :
:  ;
; 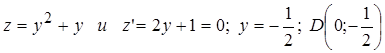 – cтационарная точка. Вычисляем
– cтационарная точка. Вычисляем 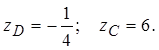
На линии  :
:  и
и  ;
;  – стационарная точка,
– стационарная точка, 
Сопоставляя все полученные значения функции  , заключаем, что
, заключаем, что 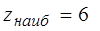 в точках
в точках  и С(0; –3),
и С(0; –3),  в точке
в точке  .
.
Для решения задачи 3 необходимо изучить пункт 8 программы.
Пример 16. Даны: функция  , точка
, точка 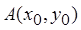 и вектор
и вектор  . Найти: 1) grad z в т.
. Найти: 1) grad z в т.  ; 2) производную в точке
; 2) производную в точке  по направлению вектора
по направлению вектора 

Решение. 1) Градиент функции  имеет вид grad
имеет вид grad  .
.
Вычисляем частные производные в точке 

Таким образом, grad z 
2) Производная по направлению вектора  , определяется по формуле
, определяется по формуле

где  – угол, образованный вектором
– угол, образованный вектором  с осью
с осью 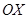 . Тогда
. Тогда
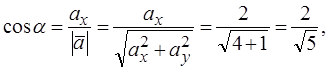

Используя значения производных в точке  , найденные ранее, получим
, найденные ранее, получим
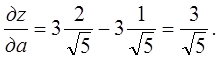
Перед решением задачи 4 необходимо изучить пункты 10 – 15, программы.
Пример 17. Вычислить объем тела, ограниченного поверхностями

Решение. Если область определена неравенствами

то объем тела  находится по формуле
находится по формуле

Для определения пределов интегрирования сделаем чертеж данного тела и его проекции на плоскость XOY (рис 2а и 2б).
Следует обратить внимание на то, что для переменной x границами являются наибольшее и наименьшее значения в заданной области, т.е.  .
.

Рис. 2а
Переменная y является функцией переменной x. На рисунке видно, что область D ограничена снизу кривой  , а сверху – кривой
, а сверху – кривой  . Следовательно,
. Следовательно,  .
.

Рис.2б
Аналогично, из рисунка тела видно, что оно снизу ограничено плоскостью  , а сверху поверхностью
, а сверху поверхностью 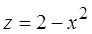 . Таким образом, переменная z является функцией двух переменных x и y, и
. Таким образом, переменная z является функцией двух переменных x и y, и 

Перед решением задачи 5 необходимо изучить пункты 16 – 22 программы.
Пример 19. Вычислить криволинейный интеграл

вдоль 1) ломаной 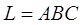 от точки
от точки 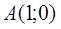 до точки
до точки  , где
, где  ;2) дуги эллипса
;2) дуги эллипса 


Решение. Пусть кривая L задана уравнениями в параметрической форме  . Пусть точкам M и P этой кривой соответствуют значения параметра t
. Пусть точкам M и P этой кривой соответствуют значения параметра t  соответственно. Тогда
соответственно. Тогда  Если кривая задана уравнением
Если кривая задана уравнением  , причем точке M соответствует
, причем точке M соответствует  , а точке P –
, а точке P –  , то
, то

1) Криволинейный интеграл вдоль ломаной L можно разбить на сумму двух интегралов: вдоль отрезков AB и BC. Запишем уравнение прямой, проходящей через две точки A и B

Найдем производную 
Уравнение отрезка BC имеет вид  . В этом случае
. В этом случае  Таким образом,
Таким образом,


2) Кривая задана в параметрическом виде. Найдем
производные
 .
.
Тогда

Приложение 1
Таблица производных
I. (С)¢ = 0.
II.  в частности
в частности 
III. (log а х)¢ =  log а е, в частности (ln х)¢ =
log а е, в частности (ln х)¢ =  .
.
IV.  в частности,
в частности, 
V. (sin х)¢ = cos х. VI. (cos х)¢ = - sin х.
vii. ( )¢ =
)¢ =  VIII. (ctg x)¢=
VIII. (ctg x)¢= 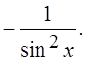
IX. (arcsin х)¢ =  . X. (arccos x)¢ =
. X. (arccos x)¢ =  .
.
XI.(arctg x)¢ =  . XII.(arcctg x)¢ =
. XII.(arcctg x)¢ =  .
.
XIII. (sh х)¢ = ch х. XIV. (ch х)¢ = sh х.
XV. (th x) ¢ =  XVI. (cth x) ¢ =
XVI. (cth x) ¢ = 
Приложение 2
Таблица интегралов
I. 
II. 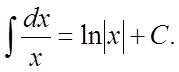
III. 
IV. 
V. 
VI. 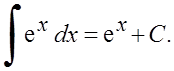
VII. 
VIII. 
IX. 
X. 
XI. 
 .
.
XII. 
XIII. 
XIV. 