Определение критической скорости вращающегося вала
Цель работы: определить теоретически и экспериментально критическую скорость вращающегося вала при различном расположении дисков относительно опор и сравнить полученные данные. Сделать выводы о причинах отклонения расчетных и экспериментальных данных.
Краткие теоретические сведения
Поперечные колебания, возникающие при вращении вала, вызывают вибрацию всей конструкции и при значительной величине амплитуд колебаний могут привести к быстрому разрушению подшипников и вала. Скорость, при которой возникают наибольшие поперечные колебания вала, называется КРИТИЧЕСКОЙ.
Рассмотрим вращение вала с одним круглым диском, центр массы которого с расположен с эксцентриситетом е по отношению к оси вала.
При вращении вала появляется центробежная
сила, которая вызывает прогиб вала на величину х.
Реакция изогнутого вала будет пропорциональна
прогибу: R = kx.
Рассматривая условие равновесия вала под
действием центробежной силы и реакции
изогнутого вала, получаем: m· (x+a) ·ω2 = kx, (1)
где ω – угловая скорость вращения диска, рад/с.
Решая уравнение (1), находим
. (2)
Известно, что k/m = p2. Амплитуда колебаний вала 
, (3)
где р - круговая частота собственных колебаний.
Анализируя выражение (3), легко установить, что амплитуда колебаний вала быстро растет, когда ω по величине приближается к р. Наиболее опасным является резонанс (ω = р).
Таким образом, вал достигает критической скорости тогда, когда его угловая скорость в радианах в секунду равна круговой частоте поперечных колебаний вала, т.е.
(4)
где k = 
– коэффициент жесткости, представляет собой силу, которую нужно приложить к валу для того, чтобы получить деформацию, равную единице длины; m – сосредоточенная масса на валу, m = m1+0,5mв,
m1 – масса диска, равная 2,8 кг; mв – масса вала, равная 0,5 кг; g – ускорение силы тяжести, 9.81 м/с2;
δ – статический прогиб вала, м,
; (5)
F – сила, на линии действия которой определяется прогиб вала, Н, F = mg;
a, b, L – размеры, показанные на рисунке, м;
Е – модуль упругости стали, Е = 2,1·1011 Па;
J – момент инерции сечения вала, J = π·d4 / 64;
d = 0,012 м – диаметр вала.
Порядок выполнения работы
2.1. Определить критическую скорость вала по формулам для следующих случаев:
а) диск расположен на равном расстоянии от опор: L = 550 мм; a = b = 275 мм; m = m1 + 0,5mв;
b) диск смещен от середины вала: L = 550 мм; a = 325 мм; b = 225 мм; m = m1 + 0,5mв.
2.2. Определить критическую скорость вращения вала экспериментально. Для этого:
а) запустить установку и поворотом рукоятки прибора ЛАТР -2М увеличить скорость вращения вала. При загорании лампы «Резонанс» записать по шкале тахометра величину скорости. Работа вала в режиме резонанса не должна продолжаться более 5 секунд. Для выхода из зоны резонанса продолжают увеличивать скорость и второй раз записывают ее значение в момент затухания лампы «Резонанс». Затем, уменьшая скорость вращения вала, регистрируют ее аналогичным образом при загорании и затухании лампы. Опыт повторяют по 3 раза при размещении диска на середине вала и при его расположении на расстоянии 325 мм от опоры со стороны электродвигателя;
б) определить критическую частоту вращения по формуле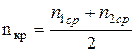 
,
где n1ср – среднее значение частоты вращения в момент входа вала в резонансную зону; n2ср – то же при выходе из резонансной зоны.
2.3. Заполнить таблицу расчетных и экспериментальных данных:
| I Таблица экспериментальных данных | ||||||||||
| Расположение диска на валу | Критическая частота вращения, об/мин | Угловая скорость, с-1 | ||||||||
| № п/п | В момент входа в зону резо нанса- n1 | В момент выхода из зоны резо нанса- n2 | n1ср | n2ср | nкр | ωкр= π·nкр/30 | ||||
| Диск на середине вала: a = b = 275 мм | ||||||||||
| Диск смещен: a = 325 мм, b = 225 мм | ||||||||||
| II Теоретический расчет | ||||||||||
| № п/п | Формулы | Результаты расчета | ||||||||
| Диск на середине вала: a = b = 275 мм | Диск смещен: a = 325 мм, b = 225 мм | |||||||||
| m = | ||||||||||
| F = | ||||||||||
| J = | ||||||||||
| δ = | ||||||||||
| k = | ||||||||||
| ωкр = | ||||||||||
2.4. Сравнить расчетные значения критических скоростей с экспериментальными и сделать выводы:
_____________________________________________________________________________________________
_____________________________________________________________________________________________
_____________________________________________________________________________________________
2.5. На отдельном листе бумаги формата А4 построить график по формуле (3) изменения амплитуд колебаний Х (ось ординат) в зависимости от отношения р/ω (ось абсцисс). Для построения задаются последовательно значениями р/ω от 0,1 до 2.
3. Контрольные вопросы
3.1. Дать определение критической скорости.
3.2. При каком условии вал достигает критической скорости?
3.3. Как зависит частота свободных колебаний от коэффициента жесткости?
3.4. Как уменьшить вредное влияние критической скорости (резонанса);
Выполнил: ст. _______________________________ гр. ___________ Принял: ________________________________