Необходимым условием отнесения кристаллов к кубическойсингонии является присутствие четырех осей третьего порядка - 4L3.
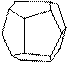
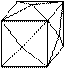
Элементарная ячейка кристаллов кубической сингонии имеет форму куба и обладает наивысшей симметрией (рис. 13). Координатные оси X, Y, Z располагаются под углом 90° друг к другу.
Параметры элементарной ячейки: a0 =b0=c0; a=b=g=90°
 |
Рис. 13. Элементарная ячейка кристаллов кубической сингонии.
В кубической сингонии выделяется пять классов симметрии:
1. 3L4 4L3 6L2 9P C
2. 3L4 4L3 6L2
3. 4L3 3 L2 6P
4. 4L3 3 L2 3P C
5. 4L3 3 L2
Для кристаллов кубической сингонии характерен изометрический (равновеликий) облик.
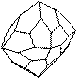
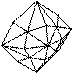
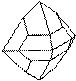
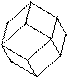
Среди простых форм кристаллов этой сингонии выделяются основные и производные. Свое название они получают по числу и форме граней (табл. 1, рис. 14).
Таблица 1.
Простые формы кристаллов кубической сингонии
| № | Основные формы | Производные формы | Кол-во граней | Форма грани |
| Тетраэдр | Равносторонний треугольник | |||
| Тригонтритетраэдр | Равнобедренный треугольник | |||
| Тетрагонтритетраэдр | Четырехугольник | |||
| Пентагонтритетраэдр | Несимметричный пятиугольник | |||
| Тригонгексатетраэдр (гексатетраэдр) | Разносторонний треугольник | |||
| Октаэдр | Равносторонний треугольник | |||
| Тригонтриоктаэдр | Равнобедренный треугольник | |||
| Тетрагонтриоктаэдр | Четырехугольник | |||
| Пентагонтриоктаэдр | Несимметричный пятиугольник | |||
| Тригонгексаоктаэдр (гексаоктаэдр) | Разносторонний треугольник | |||
| Гексаэдр (куб) | Квадрат | |||
| Тригонтетрагексаэдр (пирамидальный куб) | Равнобедренный треугольник | |||
| Ромбо-додекаэдр | Ромб с углами наклона 45° к двум координатным осям и параллельный третьей | |||
| Пентагон-додекаэдр | Симметричный пятиугольник с углами наклона 30° и 60° к двум координатным осям и параллельный третьей | |||
| Дидодекаэдр | Четырехугольник |
Ориентировка кристаллов при проектировании.
С координатными осями XYZ совмещают 3L4 (1 и 2 классы симметрии) или 3L2 (3 - 5 классы симметрии).
Единичная грань - грань октаэдра или тетраэдра - отсекает равные единичные отрезки на координатных осях. Если единичная грань в кристалле отсутствует, то можно в качестве единичных выбрать отрезки любой одинаковой длины по X, Y, Z.
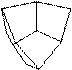
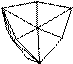
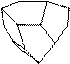
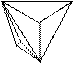
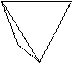 1. 2. 3. 4. 5.
1. 2. 3. 4. 5.
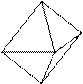 | 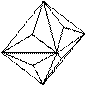 | 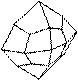 |  |  | |||||
6. 7. 8. 9. 10.
 | |||
 | |||
 11. 12. 13. 14. 15.
11. 12. 13. 14. 15.
РАБОТА 6
СРЕДНЯЯ КАТЕГОРИЯ
К средней категории относятся гексагональная, тетрагональная и тригональная сингонии.
Необходимым условием отнесения кристаллов к средней категории является наличие одной оси высшего порядка соответственно: L6, L4, L3. Вместо L6 и L4 могут присутствовать зеркально-поворотные оси шестого и четвертого порядка.
Зеркально-поворотной осью шестого порядка является прямая линия, при вращении вокруг которой на 360° кристалл через 60° трижды совмещается с первоначальным положением и трижды со своим зеркальным отражением.
 Зеркально-поворотная ось шестого порядка является простой осью третьего порядка, но не наоборот.
Зеркально-поворотная ось шестого порядка является простой осью третьего порядка, но не наоборот.
 Обозначается ось - L36.
Обозначается ось - L36.
На проекции ось изображается в виде -
Зеркально-поворотной осью четвертого порядка является прямая линия, при вращении вокруг которой на 360° кристалл через 90° дважды совмещается с первоначальным положением и дважды со своим зеркальным отражением.
Зеркально-поворотная ось четвертого порядка является простой осью второго порядка, но не наоборот.
 Обозначается ось - L24.
Обозначается ось - L24.
На проекции ось изображается в виде -
 |
ГЕКСАГОНАЛЬНАЯ СИНГОНИЯ
Необходимым условием отнесения кристаллов к гексагональной сингонии является наличие одной оси шестого порядка L6 или зеркально-поворотной оси шестого порядка L36.
Элементарная ячейка кристаллов гексагональной сингонии имеет форму шестигранной призмы (рис. 15). Для удобства пространственной ориентировки кристаллов гексагональной сингонии вводится дополнительная пространственная ось U. Таким образом, выделяется четыре координатных оси X, Y, U, Z. Оси X, Y, U располагаются в горизонтальной плоскости под углом 120°

|
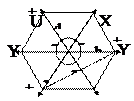 а.
а.
Рис. 15. Элементарная ячейка кристаллов гексагональной и тригональной сингонии: а - общий вид; б - вид сверху;
В гексагональной сингонии выделяется семь классов симметрии:
1. L66L2 7P C
2. L6 6L2
3. L6 6P
4.L6 P C
5. L6
6. L36 3L2 3P C
7. L36 C
Простые формы кристаллов гексагональной сингонии (рис. 16):
Различают открытые и закрытые простые формы. Открытые – состоят из граней не полностью ограничивающих пространство и встречаются только в комбинациях с другими простыми формами.
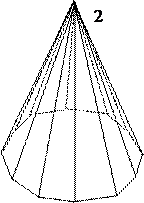
1. Гексагональная пирамида - 6 наклонных граней, сходящихся в одной вершине, через которую проходит L6. Сечение перпендикулярное ей - правильный шестиугольник.
2. Дигексагональная пирамида - 12 наклонных граней, образующих гексагональную пирамиду, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L6 , имеет вид равностороннего 12-угольника с углами, равными через один.
3. Гексагональная бипирамида - 12 наклонных граней, имеющих форму равнобедренного треугольника и образующих две одинаковые пирамиды, сложенные основаниями.
4. Дигексагональная бипирамида - 24 наклонных грани, образующих две одинаковые дигексагональные пирамиды, сложенные основаниями.
5. Гексагональная призма - 6 вертикальных граней параллельных L6 и попарно параллельных друг другу, поперечное сечение имеет вид правильного шестиугольника.
6. Дигексагональная призма - 12 вертикальных граней, образующих гексагональную призму, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L6 , имеет вид равностороннего 12-угольника с углами, равными через один.
7. Гексагональный трапецоэдр - 12 наклонных граней, имеющих форму 4-угольника с двумя равными смежными сторонами. Эта форма похожа на бипирамиду, у которой нижняя часть относительно верхней расположена асимметрично. Не имеет плоскостей и центра симметрии.
8. Ромбоэдр - 6 наклонных граней, имеющих форму ромба. Чередуясь, три из них сходятся к верхней вершине кристалла, три - к нижней. Характеризуется наличием зеркально-поворотной оси L36.
9. Гексагональный скаленоэдр - 12 граней, сгруппированных попарно, каждая из которых имеет вид разностороннего треугольника. Три пары нижних граней располагаются симметрично между тремя парами верхних. Эта простая форма характеризуется наличием зеркально-поворотной оси L36.
10. Пинакоид - 2 равных параллельных грани, имеющих любую форму. Встречается только в комбинации, например с призмой («основания» призмы).
11. Моноэдр - 1 грань, имеющая любую форму. Встречается только в комбинации, например с пирамидой («основание» пирамиды).
Ориентировка кристаллов при проектировании.
С координатными осями XYU совмещают:
- либо три оси L2 (1, 2, 6 классы симметрии);
- либо перпендикуляры к плоскостям симметрии (3 класс);
- либо направления, параллельные трем ребрам, расположенным под углом 120° друг к другу (4, 5, 7 классы).
С координатной осью Z совмещают оси симметрии L6 или L36.
Единичная грань - грань гексагональной пирамиды, бипирамиды или ромбоэдра.
Грани простых форм, принимаемые за единичные, в сложных кристаллах могут быть ориентированы по разному относительно горизонтальных осей координат. В соответствии с этим различают формы I и II рода.
 Единичная грань формы первого рода пересекает три горизонтальных координатных оси. Единичные отрезки, отсекаемые на осях X и Y равны, а отрезок, отсекаемый на оси U - вдвое меньше. Такая грань проектируется в точку I и имеет символ (1121).
Единичная грань формы первого рода пересекает три горизонтальных координатных оси. Единичные отрезки, отсекаемые на осях X и Y равны, а отрезок, отсекаемый на оси U - вдвое меньше. Такая грань проектируется в точку I и имеет символ (1121).
 Единичная грань формы второго рода пересекает две горизонтальные координатные оси и параллельна третьей. Такая грань проектируется в точку II и имеет символ (1011).
Единичная грань формы второго рода пересекает две горизонтальные координатные оси и параллельна третьей. Такая грань проектируется в точку II и имеет символ (1011).
В обоих случаях величина единичных отрезков по X, Y, U одинакова.
Величина единичных отрезков по оси Z не равна единичным отрезкам по X, Y и U.
В комбинациях могут встречаться простые формы третьего рода, грани которых проектируются в точку III. Такие грани отсекают на всех координатных осях различные по величине отрезки и единичными быть не могут. При наличии в кристалле форм третьего рода отсутствуют оси симметрии L2 и вертикально расположенные плоскости симметрии (4, 5 и 7 классы симметрии).
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
Рис. 16. Простые формы кристаллов гексагональной сингонии.
Необходимым условием отнесения кристаллов к тетрагональной сингонии является наличие одной оси четвертого порядка L4 или зеркально-поворотной оси четвертого порядка L24.
Элементарная ячейка кристаллов тетрагональной сингонии имеет форму параллелепипеда с квадратным сечением (рис. 17). Координатные оси X, Y, Z располагаются под углом 90° друг к другу.
Параметры элементарной ячейки: a0 =b0¹c0; a=b=g=90°
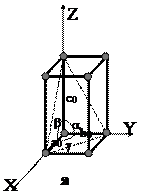 | |||
 | |||
Рис. 17. Элементарная ячейка кристаллов тетрагональной сингонии:
а -общий вид; б - вид сверху.
В тетрагональной сингонии выделяется семь классов симметрии:
1. L4 4L2 5P C
2. L4 P C
3. L4 4P
4. L4 4L2
5. L4
6. L24 2L2 2P
7. L24
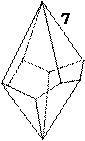
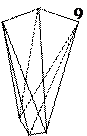
Простые формы кристаллов тетрагональной сингонии (рис. 18):
1. Тетрагональная пирамида - 4 наклонных грани, сходящихся в одной вершине, через которую проходит L4. Сечение перпендикулярное ей - квадрат.
2. Дитетрагональная пирамида - 8 наклонных граней, образующих тетрагональную пирамиду, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L4 , имеет вид равностороннего 8-угольника с углами, равными через один.
3. Тетрагональная бипирамида - 8 наклонных граней, имеющих форму равнобедренного треугольника и образующих две одинаковые пирамиды, сложенные основаниями.
4. Дитетрагональная бипирамида - 16 наклонных граней, образующих две одинаковые дитетрагональные пирамиды, сложенные основаниями.
5. Тетрагональная призма - 4 вертикальных грани, параллельных L4 и попарно параллельных друг другу, поперечное сечение имеет вид квадрата.
6. Дитетрагональная призма - 8 вертикальных граней, образующих тетрагональную призму, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L4 , имеет вид равностороннего 8-угольника с углами, равными через один.
7. Тетрагональный трапецоэдр - 8 наклонных граней, имеющих форму 4-угольника с двумя равными смежными сторонами. Эта форма похожа на бипирамиду, у которой нижняя часть относительно верхней расположена асимметрично. Эта простая форма не имеет плоскостей и центра симметрии.
8. Тетрагональный тетраэдр - 4 наклонных грани, имеющих форму равнобедренного треугольника. Для этой простой формы характерно наличие зеркально-поворотной оси четвертого порядка L24.
9. Тетрагональный скаленоэдр - 8 наклонных граней, сгруппированных попарно, каждая из которых имеет вид разностороннего треугольника. Две пары нижних граней располагаются симметрично между двумя парами верхних. Для этой простой формы характерно наличие зеркально-поворотной оси четвертого порядка L24.
10. Пинакоид.
11. Моноэдр.
 | |||||||||||||||||
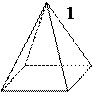 | |||||||||||||||||
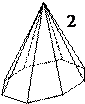 |  | ||||||||||||||||
 | |||||||||||||||||
 | |||||||||||||||||
 |  | ||||||||||||||||
 | |||||||||||||||||
Рис. 18. Простые формы кристаллов тетрагональной сингонии.
Ориентировка кристаллов при проектировании.
С координатными осями X,Y совмещают:
- либо оси L2 (в 1, 4 и 6 классах симметрии);
- либо перпендикуляры к вертикальным плоскостям симметрии (в 3 классе симметрии);
- либо направления, параллельные двум взаимно перпендикулярным ребрам (в 2, 5 и 7 классах симметрии).
С координатной осью Z совмещают оси симметрии L4 или L24.
Единичная грань - грань тетрагональных пирамиды, бипирамиды и тетраэдра.
ТРИГОНАЛЬНАЯ СИНГОНИЯ
Необходимым условием отнесения кристаллов к тригональной сингонии является наличие одной оси третьего порядка L3 .
Элементарная ячейка кристаллов тригональной сингонии аналогична таковой у гексагональной сингонии.
В тригональной сингонии выделяется пять классов симметрии:
1. L3 3L2 4P
2. L3 3L2
3. L3 3P
4.L3 P
5. L3
Характерно, что ни в одном из классов нет центра симметрии.
Простые формы кристаллов тригональной сингонии (рис. 19):
1. Тригональная пирамида - 3 наклонных грани, сходящихся в одной вершине, через которую проходит L3. Сечение перпендикулярное ей - равносторонний треугольник.
2. Дитригональная пирамида - 6 наклонных граней, образующих тригональную пирамиду, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L3 , имеет вид равностороннего 6-угольника с углами, равными через один.
3. Тригональная бипирамида - 6 наклонных граней, образующих две одинаковые пирамиды, сложенные основаниями. Сечение перпендикулярное L3, имеет вид равностороннего треугольника.
4. Дитригональная бипирамида - 12 наклонных граней, образующих две одинаковые дитригональных пирамиды, сложенные основаниями.
5. Тригональная призма - 3 вертикальных грани, параллельных L3, поперечное сечение имеет вид равностороннего треугольника.
6. Дитригональная призма - 6 вертикальных граней, образующих тригональную призму, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L3, имеет вид равностороннего 6-угольника с углами, равными через один.
7. Тригональный трапецоэдр - 6 наклонных граней, имеющих форму 4-угольника с двумя равными смежными сторонами. Эта форма похожа на бипирамиду, у которой нижняя часть расположена асимметрично верхней и поэтому не имеет плоскостей симметрии.
8. Пинакоид.
9. Моноэдр.
 | |||||
 | |||||
 | |||||
Рис. 19. Простые формы кристаллов тригональной сингонии.
В сложных формах кристаллов тригональной сингонии могут участвовать простые формы гексагональной сингонии.
Ориентировка кристаллов при проектировании.
С осью Z совпадает L3. В остальном ориентировка аналогична кристаллам гексагональной сингонии.
Единичная грань - грань тригональных пирамиды или бипирамиды. В сложных формах, также как и в гексагональной сингонии, различают формы 1-го, 2-го и 3-го рода.
РАБОТА 7
НИЗШАЯ КАТЕГОРИЯ
К низшей категории относятся ромбическая, моноклинная и триклинная сингонии.
Необходимым условием отнесения кристаллов к низшей категории является отсутствие осей симметрии высших порядков (L6, L4, L3), наличие только осей симметрии второго порядка - L2 или вообще отсутствие каких-либо элементов симметрии.
РОМБИЧЕСКАЯ СИНГОНИЯ
Необходимым условием отнесения кристаллов к ромбической сингонии является наличие не менее трех элементов симметрии (осей второго порядка и плоскостей, не считая центра).
Элементарная ячейка кристаллов ромбической сингонии имеет форму параллелепипеда с прямоугольным сечением (рис. 20). Координатные оси X, Y, Z располагаются под углом 90° друг к другу.
 Параметры элементарной ячейки: a0 ¹b0¹c0; a=b=g=90°
Параметры элементарной ячейки: a0 ¹b0¹c0; a=b=g=90°
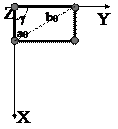 | ||||||
|
| |||||
Рис. 20. Элементарная ячейка кристаллов ромбической сингонии:
а - общий вид; б - вид сверху.
В ромбической сингонии выделяется три класса симметрии:
1. 3L2 3P C
2. 3L2
3. L2 2P
Простые формы кристаллов ромбической сингонии (рис. 21):
1. Ромбическая пирамида - 4 наклонных грани, сходящихся в одной вершине, через которую проходит L2. Сечение ей перпендикулярное - ромб.
2. Ромбическая бипирамида - 8 наклонных граней, образующих две одинаковые пирамиды, сложенные основаниями и имеющих форму разностороннего треугольника.
3. Ромбическая призма - 4 одинаковых грани попарно параллельных друг другу, поперечное сечение имеет вид ромба.
4. Ромбический тетраэдр - 4 наклонных грани, имеющих форму разностороннего треугольника. В отличие от тетраэдров кубической и тетрагональной сингоний не имеет плоскостей симметрии.
5. Диэдр - 2 равных наклонных грани, имеющих любую форму и пересекающихся наподобие крыши.
6. Пинакоид.
7. Моноэдр.
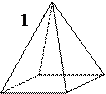 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
Рис. 21. Простые формы кристаллов ромбической сингонии.
Ориентировка кристаллов при проектировании:
В 1 и 2 классе с координатными осями XYZ совмещают оси L2 .
В 3 классе с координатной осью Z совмещают L2, а с X и Y - перпендикуляры к вертикальным плоскостям симметрии;
Единичная грань - грань ромбических пирамиды, бипирамиды и тетраэдра. Если такая грань отсутствует, символы задаются в общем виде, то есть индексы обозначаются буквами - h, k, l - по осям XYZ, которые грань пересекает. Например (hk0), (0kl), (h0l).
МОНОКЛИННАЯ СИНГОНИЯ
Необходимым условием отнесения кристаллов к моноклинной сингонии является наличие не более двух элементов симметрии, не считая центра.
Элементарная ячейка кристаллов моноклинной сингонии имеет форму наклонного параллелепипеда, две стороны которого - равные параллелограммы, две другие - прямоугольники (рис. 23). Координатные оси Y и Z располагаются под углом 90° друг к другу. Ось X перпендикулярна оси Y, а с осью Z ее положительный конец образует угол > 90°
Параметры элементарной ячейки: a0 ¹b0¹c0; a=g=90°, b > 90°
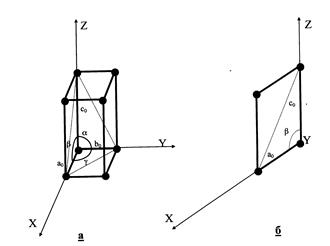
Рис. 23. Элементарная ячейка кристаллов моноклинной сингонии:
а - общий вид; б - вид на плоскость X Z.
В моноклинной сингонии выделяется три класса симметрии:
1. L2 P C
2. L2
3. P
Простые формы кристаллов моноклинной сингонии:
1. Ромбическая призма.
5. Диэдр.
6. Пинакоид.
7. Моноэдр.
Все простые формы моноклинной сингонии относятся к числу открытых, то есть не ограничивают пространство со всех сторон и потому встречаются только в комбинациях (рис. 24).
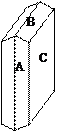 |
Рис. 24. Кристалл гипса: А, В - грани ромбических призм; С - пинакоида.
Ориентировка кристаллов при проектировании:
Ось Z располагается вертикально и параллельно ей ориентируются характерные грани кристалла, чаще всего удлиненные грани ромбической призмы.
В 1 и 2 классе с координатной осью Y совмещают ось L2 , а X и Z располагаются в плоскости, перпендикулярной L2 (в первом классе это плоскость симметрии), ось X - параллельна наклонным ребрам кристалла.
В 3 классе координатную ось Y совмещают с перпендикуляром к плоскости симметрии, а X и Z, лежащие в этой плоскости, проводятся так же, как в первом и втором классах.
На стереографической проекции ось X представлена точкой - проекцией ее отрицательного конца, лежащей внутри круга проекций на диаметре, перпендикулярном оси Y, выше центра.
Единичная грань - грань любой простой формы, пересекающая все три оси координат, задавая по ним единичные отрезки.
Если такая грань отсутствует, символы задаются в общем виде, то есть индексы обозначаются буквами - h, k, l - по осям, которые грань пересекает.
ТРИКЛИННАЯ СИНГОНИЯ
Необходимым условием отнесения кристаллов к триклинной сингонии является наличие только центра симметрии или отсутствие каких-либо элементов симметрии.
Элементарная ячейка кристаллов триклинной сингонии имеет форму наклонного параллелепипеда все стороны которого параллелограммы (рис. 25). Углы между координатными осями X, Y и Z различны и не равны 90°.
Параметры элементарной ячейки: a0 ¹b0¹c0; a ¹b ¹g ¹ 90°
 |  | ||
Рис. 25. Элементарная ячейка кристаллов триклинной сингонии:
а - общий вид; б - вид на плоскость X Z.
В триклинной сингонии выделяется 2 класса симметрии:
1. C.
2. Отсутствие элементов симметрии.
Простые формы кристаллов триклинной сингонии:
1. Пинакоид.
2. Моноэдр.
Все простые формы триклинной сингонии встречаются только в комбинациях.
Ориентировка кристаллов при проектировании.
За координатные оси X, Y, Z выбираются направления, параллельные наиболее развитым граням или ребрам кристалла, углы между которыми не равны 90°. Ось Z должна располагаться вертикально, тогда X и Y будут наклонными относительно горизонтальной плоскости проекции. Проекции осей X и Y представляют собой точки в круге проекций.
Единичная грань - грань любой простой формы, пересекающая все три оси координат, определяя по ним величину единичных отрезков.
Часто такая грань отсутствует и символы задаются в общем виде аналогично моноклинной сингонии.
Правила установки кристаллов всех сингоний при проектировании, их единичные грани и параметры элементарных ячеек приведены в приложении 1 на стр. 25.
Приложение 1
Установка кристаллов, единичная грань и параметры элементарной ячейки в различных сингониях
| Сингония | Направления, выбранные в качестве координатных осей | Соотноше-ние элемен-тарных отрезков | Осевые углы | Простые формы, грани которых могут быть единичными |
| Кубическая | 3L4 или 3L2 принимают за X,Y, Z | a0=b0=c0 | a=b=g=90° | тетраэдр, октаэдр |
| Гексагональная и тригональная* | L6, L36 или L3 принимают за Z, L2 за X, Y, U, если L2 нет, выбирают соответствующие им нормали к P или направления ребер | a0=b0=d0¹c0 | a=b=D=90° g1=g2=g3=120° | пирамида, бипирамида, ромбоэдр (гекс. сингония) |
| Тетрагональная | L4 или L24 принимают за Z L2 за X и Y, если L2 нет, выбирают соответствующие им нормали к P или направления ребер | a0=b0¹c0 | a=b=g=90° | пирамида, бипирамида тетраэдр |
| Ромбическая | 3L2 принимают за X, Y, Z, в классе (L2 2Р) ось L2 принимают за Z, нормали к Р - за X и Y | a0¹b0¹c0 | a=b=g=90° | пирамида, бипирамида тетраэдр |
| Моноклинная | L2 или нормаль к Р принимают за Y, направления двух ребер, перпендикулярных к Y принимают за X и Z | a0¹b0¹c0 | a=g=90° b¹90° | грань любой простой формы, пересекающая оси XYZ |
| Триклинная | Направления любых трех ребер, не лежащих в одной плоскости и не составляющих друг с другом угол 90о, принимают за X, Y, Z | a0¹b0¹c0 | a¹b¹g¹90° | грань любой простой формы, пересекающая оси XYZ |
* Обе сингонии имеют одинаковые число и расположение кристаллографических осей, а также соотношения единичных отрезков и осевых углов