ЭЛЕМЕНТЫ СИММЕТРИИ В КРИСТАЛЛАХ

 

Раздел кристаллографии, посвященный изучению внешней формы кристаллов, называется геометрической кристаллографией.

Кристаллами называются твердые тела, в которых материальные частицы - атомы, ионы, молекулы - расположены упорядоченно, по принципу узлов пространственных решеток.

В структуре пространственных решеток выделяются узлы, ряды, плоские сетки и элементарные ячейки.

Кристаллической решеткой называется пространственная решетка с наименьшим для данного минерала расстоянием между частицами.

Кристаллы (идеальные) представляют собой выпуклые многогранники, ограниченные гранями (часть плоскости - многоугольник), ребрами (линия пересечения граней) и вершинами (точка пересечения ребер).

Наличием кристаллической решетки объясняется правильная форма кристаллов и их важнейшие свойства - плоскогранность и прямореберность.

Грани реальных кристаллов параллельны плоским сеткам пространственных решеток, отличающихся большой плотностью материальных частиц (ретикулярная плотность). Ребра параллельны рядам пространственных решеток, а вершины отвечают их узлам.

Симметрия - важнейшее свойство кристаллов.Симметричными называются тела, у которых наблюдается закономерная повторяемость в расположении их частей в пространстве.

В геометрической кристаллографии рассматривается симметричное расположение граней, ребер, вершин кристаллов.

Степень симметричности кристаллов оценивается по наличию элементов симметрии - плоскостей, осей и центра симметрии.

Элементы симметрии в кристаллах разных видов могут присутствовать в различных количествах или отсутствовать.

Плоскость симметрии - делит кристалл на две зеркально равные части.

Плоскости симметрии в кристалле могут проходить:

а) через ребра;

б) перпендикулярно к ребрам через их середину;

в) через середины граней, перпендикулярно к ним;

г) через вершины.

Количество плоскостей симметрии в кристаллах может быть - от 1 до 9 (кроме 8).

Обозначение плоскости симметрии - Р.

Ось симметрии - прямая линия, при вращении вокруг которой кристалл совмещается с первоначальным положением в пространстве.

Минимальный угол на который необходимо повернуть кристалл до совмещения, называется элементарным углом поворота. Он может быть равен 180°, 120°, 90°, 60°.

Число совмещений кристалла с первоначальным положением при повороте на 360° определяет порядок оси симметрии. В соответствии с этим существуют оси второго, третьего, четвертого и шестого порядков.

Оси симметрии могут проходить:

- через середины граней;

- перпендикулярно граням;

- через середины ребер;

- перпендикулярно ребрам;

- через вершины.

Количество осей симметрии в кристаллах может быть:

- второго порядка - 1, 2, 3, 4, 6;

- третьего порядка - 1, 4;

- четвертого порядка - 1, 3;

- шестого порядка - 1

Обозначаются оси симметрии соответственно: L₂, L₃, L₄, L₆.

Центр симметрии (инверсии) - точка, равноудаленная от соответствующих противоположных граней, ребер и вершин кристалла. Центр симметрии совпадает с центром тяжести кристалла.

Практически наличие центра симметрии определяется следующим образом: если каждой грани кристалла соответствует равная, противоположная и параллельная грань, центр симметрии есть. Если хотя бы для одной грани нет равной, противоположной и параллельной - центра симметрии нет.

Центр симметрии может быть только один.

Обозначается центр симметрии - С.

 

Каждый кристалл характеризуется строго определенным набором элементов симметрии.

Разберем пример определения элементов симметрии кристалла галита, имеющего форму куба (рис. 1).

Если вращать кристалл вокруг линии, проходящей через середины противоположных граней, то при повороте на 360°, он четыре раза совместится со своим первоначальным положением в пространстве. Таким образом, эта линия является осью симметрии четвертого порядка(L₄). Поскольку граней шесть и через каждую пару можно провести L₄, то всего в кристалле три оси симметрии четвертого порядка (3L₄).

Линия, проходящая через противоположные вершины, является осью симметрии третьего порядка (L₃). Поскольку вершин восемь и через каждую пару можно провести L₃, то всего в кристалле четыре оси симметрии третьего порядка (4L₃).

Линия, проходящая через середины двух противоположных ребер, является осью симметрии второго порядка (L₂). Поскольку ребер двенадцать и через каждую пару можно провести L₂, то всего в кристалле шесть осей симметрии второго порядка (6L₂).

а. б.

 

Рис. 1. Расположение осей симметрии в кристалле галита:

а - четвертого и третьего порядка; б - второго порядка. Концы осей обозначены: L₂ - L₃ -; L₄ -.

На рисунке 2 показано расположение девяти плоскостей симметрии (9Р) - 4 вертикальных, 1 горизонтальная, 4 наклонных.

 

 

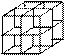Рис. 2. Расположение плоскостей симметрии в кристалле галита.

Поскольку каждой из шести граней соответствует равная и параллельная, то у кристалла имеется центр симметрии (С).

Таким образом, кристалл галита характеризуется следующим набором элементов симметрии: 3L₄, 4L₃, 6L₂, 9Р, С.

 

РАБОТА 2