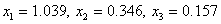Метод простой итерации или метод Якоби
Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:
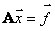 ,
,
где  ,
, 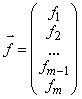 ,
, 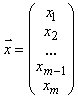 .
.
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
 (1),
(1),
Теперь, задав нулевое приближение 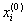 , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
, по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
 (2)
(2)
Аналогично находятся следующие приближения 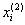 , где в (2) вместо
, где в (2) вместо 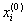 необходимо подставить
необходимо подставить 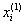 .
.
Или в общем случае:
 . (3)
. (3)
или 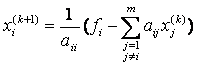
Условие окончания итерационного процесса 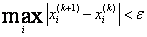 .
.
Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. 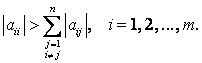 , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
, то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут 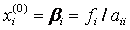 или
или 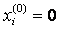 .
.
Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.
Пример.
Решить систему линейных уравнений с точностью 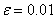 :
:
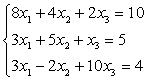
| x1 | ||||||||
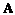 = =
| 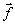 = =
| 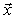 = =
| x2 | |||||
| –2 | x3 |
Решение прямыми методами, например, обратной матрицей, даёт решение:
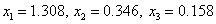 .
.
Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: 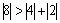 ,
, 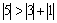 ,
, 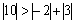 .
.
Приводим систему уравнений к виду (1):
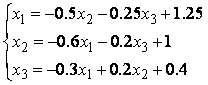 .
. 
Начальное приближение 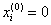 . Дальнейшие вычисления оформим в виде таблицы:
. Дальнейшие вычисления оформим в виде таблицы:
| k | x1 | x2 | x3 | точность |
| 1.250 | 1.000 | 0.400 | 1.2500 | |
| 0.650 | 0.170 | 0.225 | 0.8300 | |
| 1.109 | 0.565 | 0.239 | 0.4588 | |
| ……… | ||||
| 0.908 | 0.287 | 0.180 | 0.2781 | |
| 1.061 | 0.419 | 0.185 | 0.1537 | |
| 0.994 | 0.326 | 0.165 | 0.0931 | |
| 1.046 | 0.370 | 0.167 | 0.0515 | |
| 1.023 | 0.594 | 0.160 | 0.2235 | |
| 0.913 | 0.582 | 0.212 | 0.1101 | |
| 0.906 | 0.505 | 0.242 | 0.0764 | |
| 0.937 | 0.495 | 0.229 | 0.0305 | |
| 0.945 | 0.516 | 0.218 | 0.0210 | |
| …… | ||||
| 0.937 | 0.523 | 0.220 | 0.0077 |
Здесь 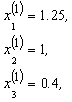
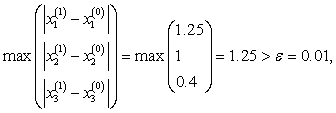

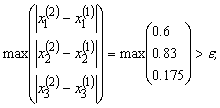
 ,
, 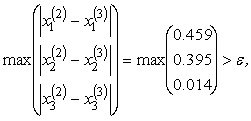
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.
Следовательно, приближенное решение имеет вид: 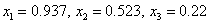
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
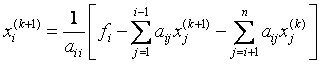
т.е. для подсчета i –й компоненты (k +1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k +1)–м шаге, новые значения первых i –1 компонент.
Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:
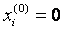
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
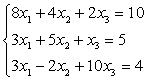
Расчетные формулы:

| k | x1 | x2 | x3 | точность |
| 1.250 | 0.250 | 0.075 | 1.2500 | |
| 1.106 | 0.321 | 0.132 | 0.1438 | |
| 1.056 | 0.340 | 0.151 | 0.0500 | |
| 1.042 | 0.344 | 0.156 | 0.0139 | |
| 1.039 | 0.346 | 0.157 | 0.0036 |
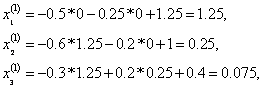
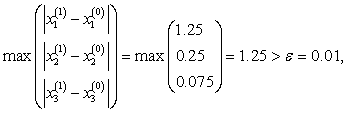

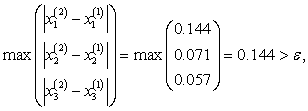
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.