Рис.6.4.
Предположим теперь, что
· наблюдатель X решил измерить длину метровой линейки, покоящейся относительно штрихованной системы координат,
· сама же система координат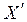 
движется относительно нештрихованной X со скоростью 
· Концы этой линейки закреплены в точках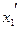 
и 
, тогда из преобразований Лоренца получаем:
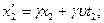
· Длина линейки в штрихованной системе (длина покоящейся линейки) равна
.
· Чтобы наблюдатель 
правильно измерил в своей системе отсчета длину движущегося предмета, он должен постараться отметить положения концов линейки в моменты времени, которые он считает совпадающими: 
, поэтому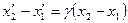 
.
· Очевидно, 
- длина линейки, которую измерит наблюдатель X. Относительно этого наблюдателя линейка движется со скоростью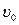 
.
· Тогда 
, или 
- длина движущейся линейки в 
раз меньше длины этой же линейки в покое. Данный факт получил название Лоренцево сокращение длины.
Одновременность событий в разных системах отсчета.
То, что один наблюдатель считает метровую линейку короче, чем другой, с точки зрения физики объясняется несовпадением для них понятия одновременности, т.е. события, одновременные для одного наблюдателя, не являются таковыми для другого.
При этом следует помнить, что для измерения длины метровой линейки положения обоих ее концов следует отмечать одновременно.
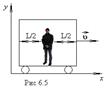Рис.6.5. Рассмотрим движущийся вагон
и покажем, что события одновременные с точки зрения неподвижного наблюдателя, не будут одновременными для наблюдателя внутри вагона. 
- длина вагона в состоянии покоя для наблюдателя 
, стоящего в центре вагона.
Предположим, что в момент времени 
наблюдатель проезжает мимо наблюдателя X, который стоит рядом с железнодорожным полотном.
В это время (по часам наблюдателя X) две молнии ударяют в концы вагона и оставляют следы на рельсах.
Наблюдателю X это дает хорошую возможность измерить длину 
вагона как расстояние между отметками, при этом .
Однако наблюдатель считает, что молния ударила сначала в правый конец, действительно, наблюдатель в вагоне движется навстречу свету от правой молнии и видит раньше этот свет.
Если лицо наблюдателя раньше освещается светом справа, то это означает, что свет справа достиг его раньше, и этот факт не зависит от наблюдателя. Но по мнению наблюдателя , обе вспышки молнии произошли на одинаковом расстоянии от него, и если он сначала видел вспышку справа, то он и считает, что она произошла раньше.
Если ввести еще одного наблюдателя 
, который начал двигаться из той же точки не вправо, а влево, то для него раньше произойдет левая вспышка.
Таким образом, если промежуток времени между двумя событиями короче того времени, которое необходимо для распространения света между ними, то порядок следования этих событий остается неопределенным: он зависит от скорости наблюдателя.
В таких случаях может оказаться, что будущее событие опережает предыдущее, если выбрать подходящего движущегося наблюдателя.
Интервал
Вернемся к понятию интервала между событиями.
В нештрихованной системе отсчета квадрат интервала равен
.
Будем считать, что оба события происходят с одной и той же частицей.
Тогда 
Но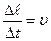 
- скорость частицы,
поэтому 
, или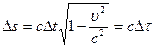 
,
где 
- промежуток собственного времени частицы между событиями.
Мы говорили, что и c являются инвариантами, следовательно, интервал 
равен произведению двух инвариантов и также является инвариантом, т.е. его величина не зависит от выбора системы отсчета и во всех инерциальных системах отсчета одинакова.
· Если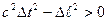 
, интервал называется вещественным.
В этом случае существует такая система отсчета , в которой 
, т.е. события, разделенные вещественным интервалом, могут быть пространственно совмещенными.
Однако не существует системы отсчета, в которой 
, т.е. события, разделенные вещественным интервалом, ни в коем случае не могут быть одновременными.
Поэтому вещественный интервал называется времениподобным.
· Если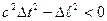 
, интервал называется мнимым.
Для таких интервалов существует система , в которой , т.е. события оказываются одновременными.
Однако не существует системы, в которой (при интервал будет вещественным), т.е.события, разделенные мнимым интервалом, не могут оказаться пространственно совмещенными.
Такой интервал называется пространственноподобным, при этом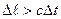 
, поэтому события не могут воздействовать друг на друга и не могут быть причинно связанными друг с другом, так как не существует воздействий, распространяющихся со скоростью, большей скорости света, порядок следования событий может быть произвольным.
Рис. 6.6 
.
· Возьмем мировую точку О некоторого события за начало отсчета времени и координат.
· Проведем в четырехмерном пространстве через эту точку взаимно перпендикулярные оси x,y,z,t. представлена плоскость x,t, для которой y= 0, z= 0.
На рисунке
· Движение частицы со скоростью 
, происходящее в трехмерном пространстве вдоль оси x, изображено прямыми 
.
· Скорость частицы не может превышать , поэтому мировые линии всех частиц, проходящий при своем движении через мировую точку О, будут лежать в пределах незаштрихованной области.
В четырехмерном пространстве этой области соответствует конус, осью которого является t. Образующие конуса представляют собой мировые линии световых сигналов. Поэтому его называют световым конусом.
- Для любой мировой точки А, лежащей в области, названной - абсолютно будущей,
- 
- интервал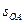 
между событиями О и А – времениподобный,
- причем в выбранной нами системе отсчета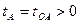 
.
Если брать системы отсчета, скорость которых относительно нашей системы меняется непрерывно, будет непрерывно меняться и промежуток времени 
. Однако, ни в одной системе отсчета не может быть равным нулю (два события, разделенные времениподобным интервалом, ни в какой системе отсчета не могут быть одновременными). Следовательно, не существует и таких систем отсчета, в которых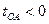 
(чтобы стать отрицательным, должен при непрерывном изменении измениться скачком).
- Таким образом, во всех системах отсчета событие А будет происходить позже события О.
- Для любой мировой точки B, лежащей в абсолютно прошедшей области,
- 
,
- и нтервал 
-времениподобный,
- однако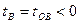 
- и во всех системах отсчета событие B предшествует событию О.
- Для любого события C или D, мировая точка которого лежит в абсолютно удаленных областях,
- 
,
- интервалы 
и 
- пространственноподобные.
- В любой системе отсчета события O и C, или O и D происходят в разных точках пространства. Понятие одновременности этих событий является относительным. В одних системах отсчета событие C (или D) происходит позже, а в других раньше события O.
Имеется одна система отсчета, в которой событие C (или D) происходит одновременно с O).