ЛЕКЦИЯ 5
НЕКОТОРЫЕ ТИПИЧНЫЕ АЛГОРИТМЫ/3,5,7,9/
------------------------------------------------------------------------------------------------------------------
Вводный комментарий
Алгоритмы поиска
Сортировка массивов
5.3.1. Вводный комментарий
5.3.2. Сортировка простыми включениями
5.3.3. Сортировка простым выбором
5.3.4. Сортировка простым обменом (метод пузырька)
Улучшенные методы сортировки
5.4.1. Сортировка включениями с убывающими приращениями
5.4.2. Сортировка с помощью дерева (пирамидальная сортировка)
5.4.3. Сортировка с разделением (быстрая сортировка)
5.4.4. Сравнение методов сортировки
5.4.5. Алгоритм поиска медианы
Алгоритмы сжатия информации
5.5.1. Основные понятия
5.5.2. Кодирование Хаффмена
5.5.3. Адаптивное сжатие
5.5.4. Кодирование Лемпела-Зива
Рекурсивные алгоритмы
5.6.1. Основные понятия
5.6.2. Типичные примеры рекурсивных алгоритмов
-----------------------------------------------------------------------------------------------------------------
Вводный комментарий
Рисунок 5.1
Алгоритмы поиска
Линейный поиск.
Дихотомию (поиск делением пополам или двоичный поиск)
Поиск в таблице.
Прямой поиск строки.
Поиск в строке.
Сортировка массивов
5.3.1. Вводный комментарий
Сортировка - это распределение элементов множества по группам в соответствии с определенными правилами.
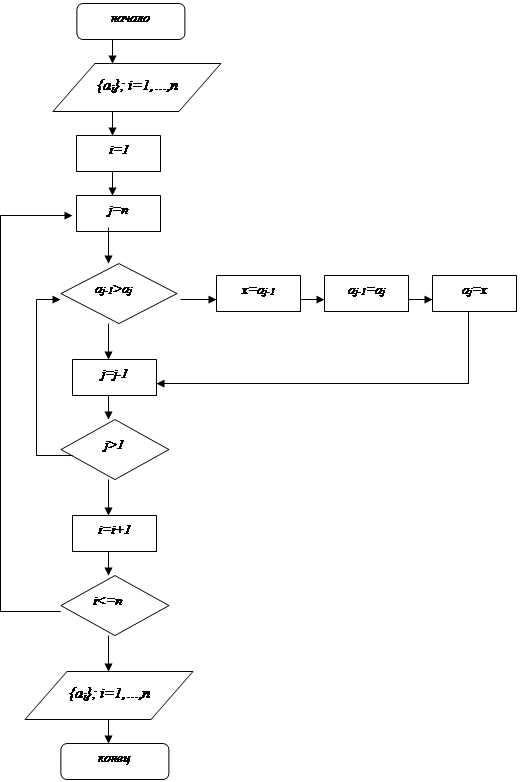
5.3.2. Сортировка простыми включениями
Таблица 5.1
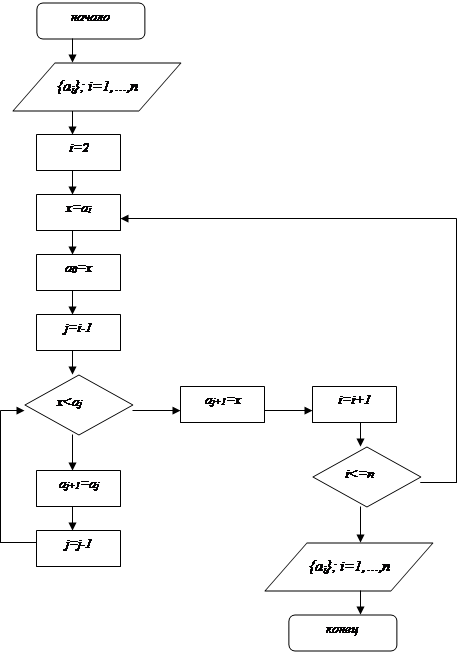
Пример упорядочения элементов числового массива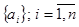 
по возрастанию методом сортировки простыми включениями представлен на рисунке 5.2.
5.3.3. Сортировка простым выбором
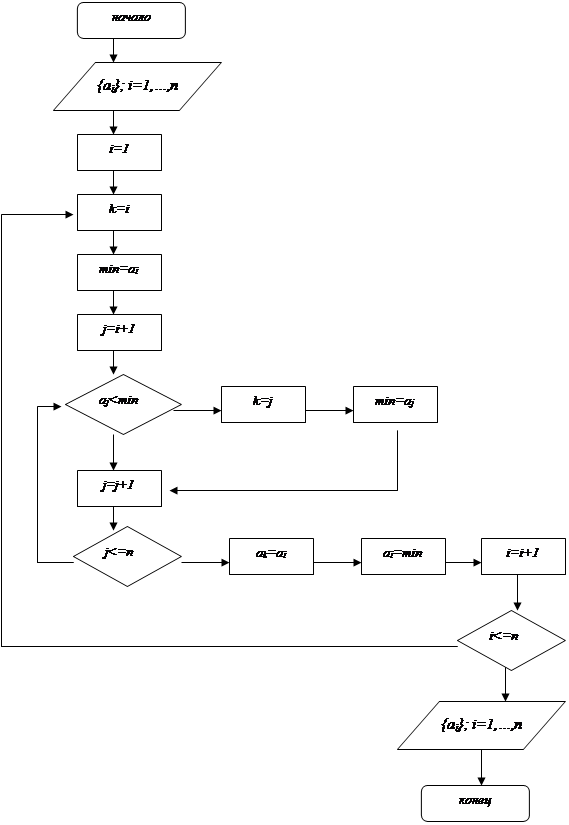
Пример сортировки простым выбором представлен на рисунке 5.3. Выполняется упорядочение по возрастанию элементов массива 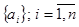, элементы удаляются из начала последовательности (находится минимальный элемент и ставится на место первого).
|
|
 |
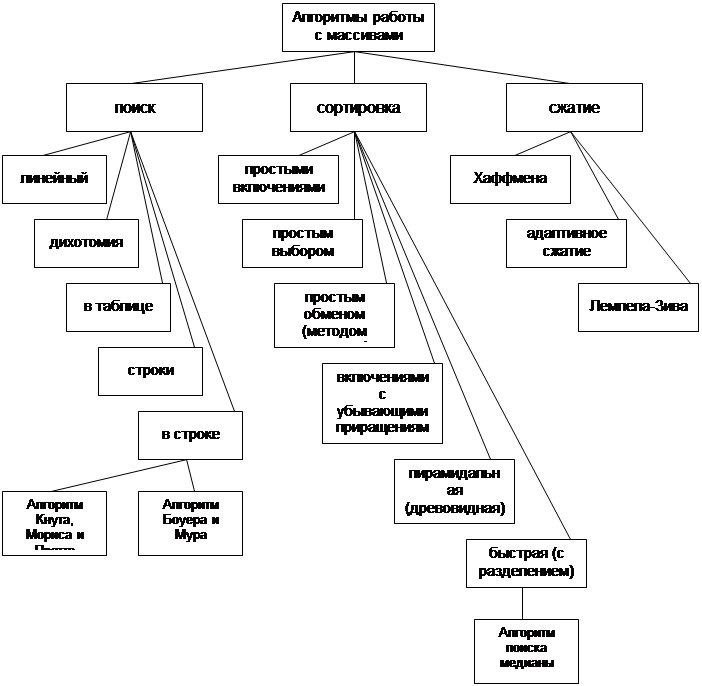Рис. 5.1. Типичные алгоритмы работы с массивами
Таблица 5.1 Иллюстрация сортировки простыми включениями
| Начальные ключи |  44
| |||||||
| i=2 | ||||||||
| i=3 |  12
| |||||||
| i=4 | ||||||||
| i=5 | ||||||||
| i=6 | ||||||||
| i=7 | ||||||||
| i=8 |
_
+
+
–
Рис. 5.2. Блок-схема сортировки простыми включениями
Иллюстрация сортировки простым выбором
| Начальные ключи |  44
| |||||||
| i=2 | ||||||||
| i=3 | 06 | 12 | 55 | 42 | 94 | 18 | 44 | 67 |
| i=4 | 06 | 12 | 18 | 42 | 94 | 55 | 44 | 67 |
| i=5 | 06 | 12 | 18 | 42 |  94
| 55 | 44 | 67 |
| i=6 | 06 | 12 | 18 | 42 | 44 | 55 | 94 | 67 |
| i=7 | 06 | 12 | 18 | 42 | 44 | 55 | 94 | 67 |
| i=8 | 06 | 12 | 18 | 42 | 44 | 55 | 67 | 94 |
+
–
+ –
–
+
Рис. 5.3. Блок-схема сортировки простым выбором
5.3.4. Сортировка простым обменом (метод пузырька)
Пример упорядочения элементов одномерного числового массива 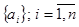по возрастанию методом сортировки простым обменом представлен на рисунке 5.4. Сравнение элементов начинается с конца последовательности.
Таблица 5.3
Иллюстрация сортировки методом пузырька
| Начальные ключи | i=2 | i=3 | i=4 | i=5 | i=6 | i=7 | i=8 |
 44
| |||||||
Таблица 5.4
|
|
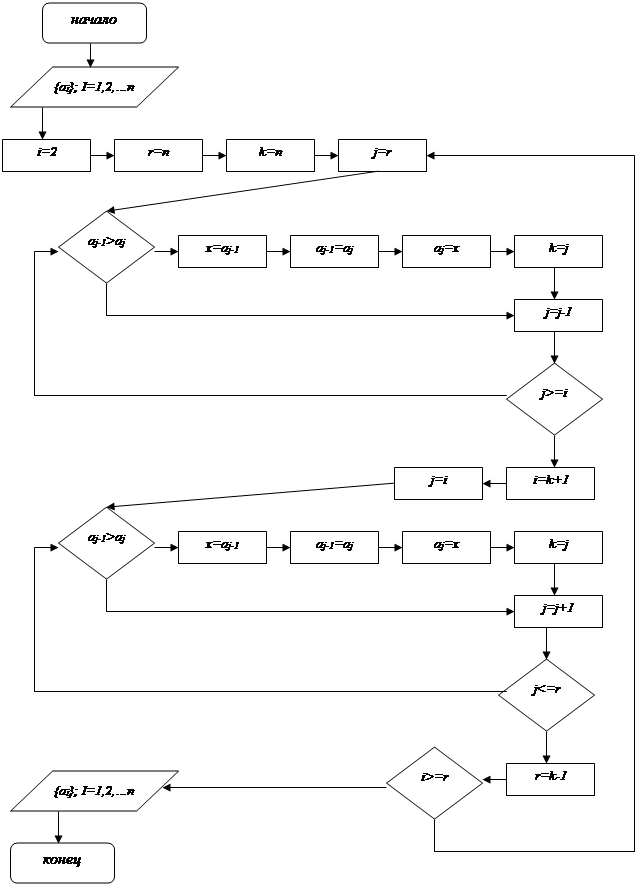
Иллюстрация шейкер-сортировки
| i=2 | i=3 | i=3 | i=4 | i=4 |
| r=8 | r=8 | r=7 | r=7 | r=4 |
| | ¯ | | ¯ | |
 44
| ||||
Улучшенные методы сортировки
5.4.1. Сортировка включениями с убывающими приращениями
В 1959 г., Д. Шелл
 |
_
+
+
_
+
_
Рис. 5.4. Блок-схема сортировки методом пузырька
 |
_
+
+
–
+
_
+
–
Рис. 5.5. Блок-схема сортировки оптимизированным методом пузырька
 |
+
–
+
_
–
+
+
–
+
–
Рис. 5.6. Блок-схема шейкер-сортировки
Пример, иллюстрирующий сортировку включениями с убывающими приращениями, представлен на рисунке 5.7.
44 55 12 42 94 18 06 67 четверная сортировка
44 18 06 42 94 55 12 67 двойная сортировка
06 18 12 42 44 55 94 67 одинарная сортировка
06 12 18 42 44 55 67 97 отсортированный массив
Рис. 5.7. Сортировка включениями с убывающими приращениями
Приращения обозначаются через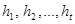 
, причем 
.
Пример упорядочения числового массива в порядке возрастания методом сортировки Шелла (рис. 5.8). Здесь t=4.
|
|
5.4.2. Сортировка с помощью дерева (пирамидальная сортировка)
Дж. Уильямс, Р. Флойд
5.4.3. Сортировка с разделением (быстрая сортировка)
К. Хоар
5.4.4. Сравнение методов сортировки
Таблица 5.5. Сравнение простых методов сортировки
| алгоритм | минимальное | Среднее | Максимальное |
| простые включения | C=n-1 M=2(n-1) | C=(n2+n-2)/4 M=(n2-9n-10)/4 | C=(n2-n)/2-1 M=(n2-3n-4)/2 |
| простой выбор | C=(n2-n)/2 M=3(n-1) | C=(n2-n)/2 M=n(ln(n)+0,75) | C=(n2-n)/2 M=n2/4+3(n-1) |
| простой обмен | C=(n2-n)/2 M=0 | C=(n2-n)/2 M=(n2-n)*0,75 | C=(n2-n)/2 M=(n2-n)*1,5 |
5.4.5. Алгоритм поиска медианы
Медианой последовательности из n элементов называется элемент, значение которого меньше или равно половины n элементов и больше или равно другой половины.
+
–
_
+
+
–
+
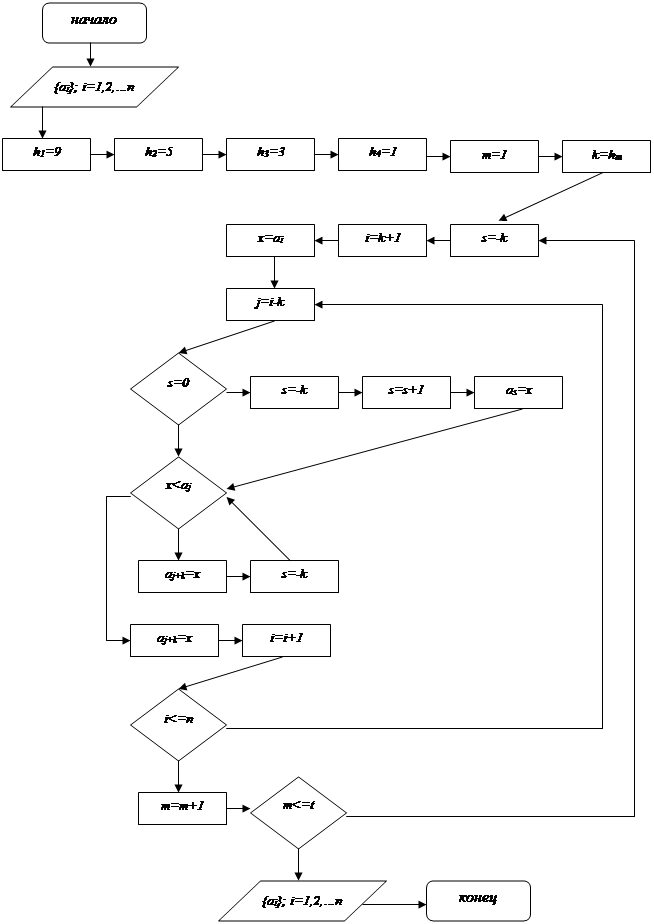
Рис. 5.8. Блок-схема сортировки Шелла