Введение
Развитие науки и техники, повышение требований к качеству продукции и эффективности производства привели к радикальному изменению требований к измерениям. Один из основных аспектов этих требований - обеспечение возможности достаточно достоверной оценки погрешности измерений. Отсутствие данных о точности измерений или недостаточно достоверные ее оценки полностью или в значительной степени обесценивают информацию о свойствах объектов и процессов, качестве продукции, об эффективности технологических процессов, о количестве сырья, продукции и т.п., получаемую в результате измерений [2]. Некорректная оценка погрешности измерений чревата большими экономическими потерями, а иногда и техническими последствиями. Заниженная оценка погрешности измерений ведет к увеличению брака продукции, неэкономичному или неправильному учету расходования материальных ресурсов, неправильным выводам при научных исследованиях, ошибочным решениям при разработке и испытаниях образцов новой техники. Завышенная оценка погрешности измерений, следствием чего, как правило, является ошибочный вывод о необходимости применения более точных средств измерений (СИ), вызывает непроизводительные затраты на разработку, промышленный выпуск и эксплуатацию СИ. Стремление максимально приблизить оценку погрешности измерений к ее действительному значению так, чтобы она при этом оставалась в вероятностном смысле "оценкой сверху", - одна из характерных тенденций развития современной практической метрологии. Эта тенденция приобретает особенно большое практическое значение там, где требуемая точность измерений приближается к точности, которую могут обеспечивать образцовые СИ и где повышение корректности оценок точности измерений по существу является одним из резервов повышения точности измерений. Погрешность измерений обусловлена, в общем случае, рядом факторов. Она зависит от свойств применяемых СИ, способов использования СИ (методик выполнения измерений), правильности калибровки и поверки СИ, условий, в которых производятся измерения, скорости (частоты) изменения измеряемых величин, алгоритмов вычислений, погрешности, вносимой оператором [2]. Следовательно, задача оценки погрешности измерений в современных условиях, в частности, технических измерений - сложная комплексная задача.
Уманская А.К. Линеаризация (моделирование)
функций преобразования средства измерения. -
Челябинск: ЮУрГУ, ПС; 2012.18с.4ил.,
библиогр. список - 1 наим.
На основе исходных данных произведена линеаризация (моделирование) функции преобразования средства измерения и рассчитаны погрешности.
Задачи
ЗАДАЧА 1.
Чувствительность СИ и предельную нестабильность чувствительности. Чувствительность СИ:
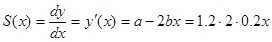
Предельная нестабильность чувствительности [1]:
ЗАДАЧА 2.
Предельные относительные погрешности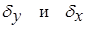 
, приведенные к выходу и ко входу СИ
Найдем погрешность выходного сигнала 
.
По определению:
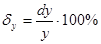
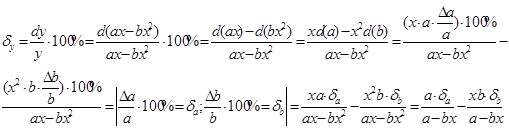
Определим значения относительной погрешности [1] при значениях входной измеряемой величины:
Найдем погрешность выходного сигнала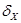 
, приведенную к выходу СИ.
По определению:
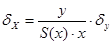
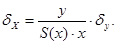, где 
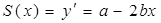
Определим значения относительной погрешности при значениях входной измеряемой величины:
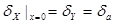
ЗАДАЧА 3.
Определить абсолютную, относительную и приведенную погрешности нелинейности при аппроксимации функции преобразования СИ в виде касательной в начальной точке.
Определить наибольшую погрешность нелинейности. Уравнение касательной имеет вид:
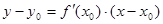
Точка, через которую проходит касательная
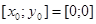
Угловой коэффициент касательной:
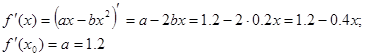
Функция линеаризации принимает вид: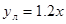 
Определим погрешности линеаризации [1]:
Абсолютная погрешность:
Относительная погрешность:
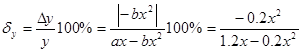
Приведенное значение погрешности (в точке x=xн):
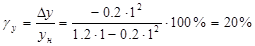
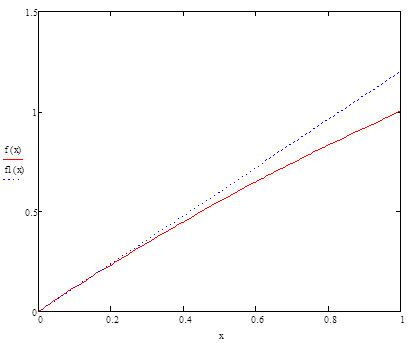
График аппроксимации функции преобразования в виде касательной в начальной точке:
ЗАДАЧА 4
Определить относительную и абсолютную погрешности нелинейности при аппроксимации функции преобразования СИ в виде хорды, проходящей через начальную и конечную точки диапазона измерения. Определить наибольшую погрешность нелинейности.
Уравнение хорды имеет вид:
Точки, через которых проходит хорда:
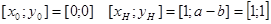
Функция линеаризации принимает вид:
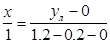
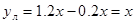
Определим погрешности линеаризации.
Абсолютная погрешность:
Относительная погрешность:
Максимальная погрешность нелинейности при xэ:
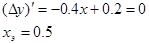
Найдем погрешность:
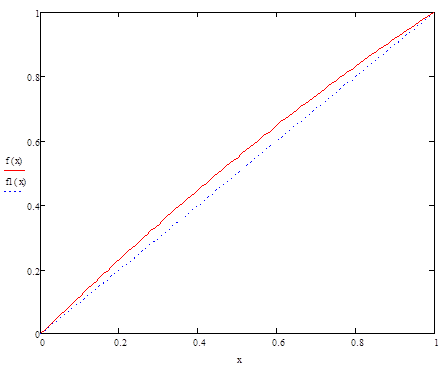
График аппроксимации функции преобразования в виде хорды, проходящей через начальную и конечную точки нашего диапазона.
ЗАДАЧА 5.
Аппроксимировать функцию преобразования СИ на интервале: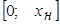 
линейной функцией вида: 
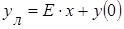, так, чтобы наибольшая погрешность линеаризации была минимальна: 
. Определить предельные относительную и приведенную погрешности линеаризации.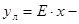 
функция аппроксимации.
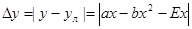- абсолютная погрешность линеаризации.
Погрешность принимает наименьшее значение в точке, в которой:
средство измерения погрешность нелинейность
Запишем условие оптимизации системы:
, где
погрешность в конце диапазона измерения:
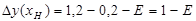
погрешность в экстремальной точке:
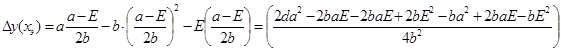
Расскроем модули и запишем уравнение:
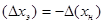
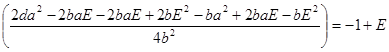
Откуда: 
Функция аппроксимации имеет вид: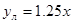 
Определим погрешность в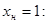 
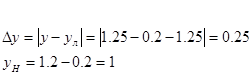
Предельная приведенная погрешность линеаризации равна:
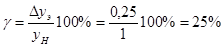
График аппроксимации функции преобразования линейной функцией вида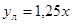 
с минимальной наибольшей погрешностью.
ЗАДАЧА 6.
Аппроксимировать функцию преобразования СИ на интервале: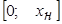 
линейной функцией вида: 
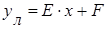, так, чтобы наибольшая погрешность линеаризации была минимальна: 
.
Определить предельные относительную и приведенную погрешности линеаризации.
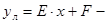функция аппроксимации.
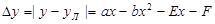-абсолютная погрешность линеаризации.
Погрешность принимает наименьшее значение в точке, в которой:
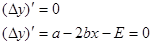
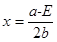
Условие оптимизации системы:
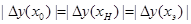, где
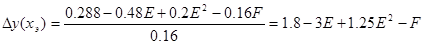
Составим систему:
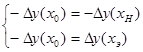
Из решения системы получим:
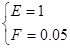
Функция аппроксимации имеет вид:
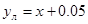
Определим погрешности.
Предельная приведенная погрешность линеаризации равна:
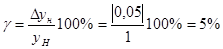
График аппроксимации функции преобразования линейной функцией вида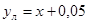 
с минимальной наибольшей погрешностью.
Заключение
Построив линейные модели функций преобразования средств измерения разными способами, мы убедились, что способ моделирования функции преобразования линейной функцией вида: 
, так, чтобы наибольшая погрешность линеаризации была минимальна, самый эффективный, т.к. в нем была наименьшая погрешность и постоянная чувствительность.
Библиографический список
1. Аксенова, Е.Н. Элементарные способы оценки погрешностей результатов прямых и косвенных измерений / учебное пособие для вузов. - М.: Изд-во Логос; Университетская книга, 2007.
2. Методический материал по применению ГОСТ 8.009-84 "ГСИ. Нормируемые метрологические характеристики средств измерений"-https://www.gosthelp.ru/text/Metodicheskijmaterialpopr.html