Понятие о СОУ и их классификация.

По дисциплине «Эконометрика»

на тему:

«Системы эконометрических уравнений».

Вопросы:

Понятие о системах одновременных уравнений (СОУ) и их классификация.

Структурная и приведенная формы модели. Проблема идентификации.

Оценивание параметров систем одновременных уравнений.

Применение систем для моделирования макроэкономических процессов.

Вопросы для самостоятельной проверки знаний по теме.

Рекомендуемая литература.

Понятие о СОУ и их классификация.

При построении регрессионных моделей с одним уравнением предполагалось, что между независимыми переменными и зависимой переменной в каждый момент времени существует только односторонняя связь: В такой ситуации зависимая переменная не оказывала ни какого влияния на переменные, входившие в правую часть модели.

Это не означает, что все факторы характеризуются как абсолютно независимые. Однако предопределяющие их значения причины не находились под воздействием явления, отражаемого переменной . Таким образом, в тенденциях развития переменных и просматривалась как бы строгая очередность. Сначала в момент t возникали явления, выражаемые независимыми в модели переменными , а затем под их влиянием формировалось явление, которое выражалось переменной .

В реальной жизни многие экономические и социальные явления развиваются, воздействуя друг на друга одновременно, так что в единичный период времени, обозначаемый индексом t, невозможно установить, какое из этих явлений первично, а какое вторично. В качестве типичного примера такой взаимосвязи обычно называют соотношение между спросом и предложением, характеризующееся в единичном интервале времени взаимным влиянием друг на друга цены и объема производства (потребления) товара при участии некоторого количества других факторов, которые можно считать независимыми.

Другой пример. При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.

В еще большей степени возрастает потребность в использовании системы взаимоствязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам. Модель национальной экономики включает в себя систему уравнений: функции потребления, инвестиций заработной платы, а также тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Так, расходы на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.

Система уравнений в эконометрических исследованиях может быть построена по-разному.

Рассмотрим разновидности систем эконометрических уравнений.

1) системы независимых уравнений:

Фактически, каждое уравнение такой системы представляет собой линейную модель множественной регрессии. Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели, характеризующие эффективность сельскохозяйственного производства, а в качестве факторов – величины, обуславливающие эту эффективность.

2) системы рекурсивных уравнений:

Каждое последующее уравнение такой системы кроме перечня независимых факторов включает в себя оцененные ранее эндогенные переменные. Примером такой системы может служить модель производительности труда и фондоотдачи.

3) системы взаимозависимых уравнений (СОУ):

В этой системе каждое уравнение содержит весь перечень экзо- и эндогенных переменных. Примером системы одновременных уравнений может служить модель динамики цены и заработной платы.

 

2. Структурная и приведенная формы модели. Проблема идентификации.

 

Структурной формой модели (СФМ) называется модель вида

Если в результате соответствующих преобразований система примет вид

то она будет называться приведенной формой модели (ПФМ).

Пример. Пусть СФМ имеет вид

Необходимо получить ПФМ. Для этого выражение для переменной из второго уравнения подставим в первое уравнение:

Если обозначить

, ,

то получим первое уравнение ПФМ

Аналогично, можно получить второе уравнение ПФМ

Замечания: 1) обычный метод наименьших квадратов не подходит для оценивания параметров структурной модели, поэтому осуществляется переход к ПФМ;

2) ПФМ по своему значению уступает СФМ, так как в последней учитывается все многообразие экономических взаимосвязей.

Параметры ПФМ являются нелинейными функциями параметров СФМ. При выполнении обратного перехода иногда возникает проблема идентификации. Идентификация – это однозначность соответствия между структурными и приведенными коэффициентами. Проблема является результатом несоответствия числа приведенных и структурных коэффициентов. С позиций идентифицируемости выделяют модели:

- точно идентифицируемые,

- неидентифицируемые,

- сверхидентифицируемые.

Модель точно идентифицируема, если параметры СФМ однозначно определяются по параметрам ПФМ. Модель неидентифицируема, если параметров СФМ больше, чем параметров ПФМ. Модель сверхидентифицируема, если параметров ПФМ больше, чем у СФМ.

Рассмотрим необходимое и достаточное условия идентифицируемости модели.

Если обозначить число эндогенных переменных в i-ом уравнении СФМ через Н, а число предопределенных переменных, которые содержатся в системе, но не входят в данное уравнение, через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

- если D+1<H, то уравнение неидентифицируемо;

- если D+1=H, то уравнение идентифицируемо;

- если D+1>H, то уравнение сверхидентифицируемо.

Это правило является необходимым, но недостаточным условием идентификации. Для идентифицируемости уравнения еще должно выполняться дополнительное условие.

Отметим эндогенные и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу. При этом, если переменная стоит в левой части уравнения, то коэффициент надо брать с обратным знаком. Тогда дополнительное условие состоит в следующем:

- если определитель полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие идентификации для данного уравнения выполнено.

Пример. СФМ задана в виде матрицы коэффициентов модели

Номер уравнения	Переменные
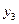
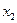
	-1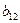
		-1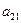
			-1

 

Необходимо записать СОУ и проверить ее на идентифицируемость.

Решение. СФМ имеет вид

Проверим необходимое и достаточное условия идентифицируемости для каждого уравнения системы:

первое уравнение:

Н=3, D=2, 2+1=3 – необходимое условие выполнено;

,

так как определитель этой матрицы равен нулю, то достаточное условие идентификации для этого уравнения не выполнено; первое уравнение неидентифицируемо;

второе уравнение:

Н=2, D=1, 1+1=2 – необходимое условие выполнено;

,

так как определитель этой матрицы отличен от нуля, а rank=2, что не меньше 3-1, то достаточное условие идентификации для этого уравнения выполнено; таким образом, второе уравнение идентифицируемо;

третье уравнение:

Н=3, D=2, 2+1=3 – необходимое условие выполнено;

,

так как определитель этой матрицы равен нулю, то достаточное условие идентификации для этого уравнения не выполнено; третье уравнение неидентифицируемо.

Вывод. В данной системе идентифицируемо только одно уравнение, следовательно, система неидентифицируема.