Момент силы и момент импульса материальной точки.

Полная механическая энергия. Консервативные системы. Закон сохранения механической энергии. Диссипация энергии. Общефизический закон сохранения и превращения энергии.

Полная механическая энергия характеризует движение и взаимодействие тел, следовательно, зависит от скоростей и взаимного расположения тел.

Полная механическая энергия замкнутой механической системы равна сумме кинетической и потенциальной энергии тел этой системы:

Консервативная система (от лат. conservo — сохраняю) — физическая система, для которой все действующие на неё внешние и внутренние непотенциальные силы не совершают работы, а все потенциальные силы стационарны,^[1][2] все связи стационарны, силы не зависят от времени.

Для такой системы верен закон сохранения энергии.

Закон сохранения энергии

Закон сохранения энергии - фундаментальный закон природы.

В ньютоновской механике закон сохранения энергии формулируется следующим образом:

• Полная механическая энергия изолированной (замкнутой) системы тел остаётся постоянной.

Другими словами:

• Энергия не возникает из ничего и не исчезает никуда, она может только переходить из одной формы в другую.

Диссипация энергии (лат. Dissipatio — рассеяние) — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. П.) В энергию неупорядоченных процессов, в конечном счёте — в теплоту. Системы, в которых энергия упорядоченного движения с течением времени убывает за счёт диссипации, переходя в другие виды энергии, например, в теплоту или излучение, называются диссипативными.

Если диссипация энергии происходит в замкнутой системе, то энтропия системы возрастает. Диссипация энергии в открытых системах, обусловленная процессами уноса энергии из системы, например, в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды.

формулировка закона сохранения механической энергии:

- полная энергия замкнутой механической системы не меняется с течением времени.

В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.

Момент силы и момент импульса материальной точки.

Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по 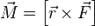определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м

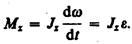Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произ­ведением:

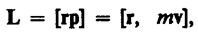Где r — радиус-вектор, проведенный из точки О в точку A, p =m v — импульс мате­риальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р.

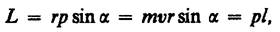
Модуль вектора момента импульса

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость.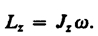

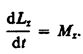уравнения динамики вращательного движения твер­дого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.