Лекция 2. Энергетические характеристики
Электростатического поля
План лекции
2.1. Работа электростатического поля
2.2. Циркуляция вектора напряженности электростатического поля. Потенциал электростатического поля и его связь с напряженностью.
2.3. Локальное описание электростатических полей.
Работа электростатического поля
Если в электростатическом поле точечного заряда Q в вакууме из точки 1 в точку 2, перемещается другой точечный заряд Q 0 (рис.2.1), то сила, приложенная к заряду Q 0 (со стороны поля заряда Q) совершает работу. Работа силы  на элементарном перемещении
на элементарном перемещении  в вакууме
в вакууме  ;
;  ;
;  и в итоге получаем
и в итоге получаем  . Работа по перемещению заряда Q 0 из "1" в "2"
. Работа по перемещению заряда Q 0 из "1" в "2"
 (2.1)
(2.1)
Из (2.1) следует, что А не зависит от траектории перемещения и по замкнутому пути равна нулю, то есть кулоновские силы – консервативны, а электростатическое поле точечного заряда является потенциальным. Согласно (2.1) так же получаем, что работа, совершаемая при перемещении электрического заряда в электростатическом поле по любому замкнутому пути "L" равна нулю, то есть
 (2.2)
(2.2)


Рис.2.1
Циркуляция вектора напряженности
Электростатического поля. Потенциал
Электростатического поля и его связь с
Напряженностью
При перемещении единичного точечного положительного заряда в электростатическом поле элементарная работа  , где
, где  – проекция Е на направление элементарного перемещения. Применяя (2.2), можно записать
– проекция Е на направление элементарного перемещения. Применяя (2.2), можно записать
 (2.3)
(2.3)
Интеграл  называют циркуляцией вектора напряженности и полученный результат (2.3) означает, что циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Так как это получено из выражения (2.2), то можно утверждать, что силовое поле, обладающее свойством (2.3), обязательно является потенциальным. Из (2.3) следует также, что линии напряженности электростатического поля не могут быть замкнутыми; они начинаются и кончаются на зарядах (соответственно положительных или отрицательных) или же уходят в бесконечность.
называют циркуляцией вектора напряженности и полученный результат (2.3) означает, что циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Так как это получено из выражения (2.2), то можно утверждать, что силовое поле, обладающее свойством (2.3), обязательно является потенциальным. Из (2.3) следует также, что линии напряженности электростатического поля не могут быть замкнутыми; они начинаются и кончаются на зарядах (соответственно положительных или отрицательных) или же уходят в бесконечность.
Ранее отмечалось (см. лекцию 4 части I, выражение 4.13), что в потенциальных полях работа консервативных сил совершается за счет убыли потенциальной энергии. Таким образом, работу (2.2) сил электростатического поля можно представить как разность потенциальных энергий которыми обладает точечный заряд Q0 в точках "1" и "2" поля заряда Q, то есть
 , (2.4)
, (2.4)
откуда следует, что потенциальная энергия заряда Q 0 в поле заряда Q в вакууме равна  . Таким образом, так же, как и в механике, здесь потенциальная энергия определяется лишь с точностью до произвольной постоянной. Обычно принято считать, что в бесконечности (при
. Таким образом, так же, как и в механике, здесь потенциальная энергия определяется лишь с точностью до произвольной постоянной. Обычно принято считать, что в бесконечности (при  )
)  (то есть С = 0) и окончательно: потенциальная энергия заряда Q 0, находящегося в поле заряда Q на расстоянии r от него равна
(то есть С = 0) и окончательно: потенциальная энергия заряда Q 0, находящегося в поле заряда Q на расстоянии r от него равна
 . (2.5)
. (2.5)
Из (2.5) следует, что при помещении в некоторую точку А в электростатическом поле поочередно зарядов Q 1; Q 2;… Q n отношение  остается постоянным, то есть может быть принято за энергетическую характеристику поля в данной точке. Эта величина
остается постоянным, то есть может быть принято за энергетическую характеристику поля в данной точке. Эта величина
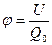 (2.6)
(2.6)
является энергетической характеристикой электростатического поля, называемой потенциалом. При Q 0 = 1 (из 2.6) имеем  , то есть потенциал
, то есть потенциал  в какой-либо точке поля определяется, как потенциальная энергия единичного положительного заряда, помещенного в рассматриваемую точку. Из (2.6 и 2.5) следует, что потенциал поля, создаваемого точечным зарядом Q в вакууме равен
в какой-либо точке поля определяется, как потенциальная энергия единичного положительного заряда, помещенного в рассматриваемую точку. Из (2.6 и 2.5) следует, что потенциал поля, создаваемого точечным зарядом Q в вакууме равен
 (2.7)
(2.7)
Согласно (2.4, 2.6 и 2.7) работу, совершаемую силами электростатического поля при перемещении заряда Q0 из точки "1" в точку "2" можно представить как
 (2.8)
(2.8)
Величина
 (2.9)
(2.9)
называется разностью потенциалов двух точек 1 и 2 в электростатическом поле и (в соответствии с (2.9)) определяется работой, совершаемой силами поля при перемещении единичного положительного заряда из одной точки поля в другую. Если перемещать заряд Q0 из произвольной точки за пределы поля (то есть в бесконечность, где по условию (2.7)  ), то согласно (2.8)
), то согласно (2.8)  2, откуда
2, откуда
 , (2.10)
, (2.10)
то есть потенциал имеет (помимо рассмотренного выше) и такой физический смысл: потенциал определяется работой по перемещению единичного положительного заряда (при удалении его) из данной точки в бесконечность. Из (2.6) следует, что в "СИ" единица потенциала 1 Вольт:

Рассмотрим перемещение единичного точечного положительного заряда из одной точки поля в другую вдоль оси Х при условии, что точки расположены бесконечно близко друг к другу. Исходя из формул механической работы в этом случае dA = Еxdх. Согласно (2.8) эта же работа  . Приравнивая оба выражения, получим
. Приравнивая оба выражения, получим
 (2.9)
(2.9)
По аналогии в декартовой системе координат (x, y, z) расположение зарядов можно записать
 , (2.10)
, (2.10)
где оператор  ;
;  – единичные векторы координатных осей x, y, z.
– единичные векторы координатных осей x, y, z.
Введем векторный дифференциальный оператор Гамильтона, обозначаемый греческой буквой 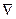 (набла) и равный в декартовой системе координат
(набла) и равный в декартовой системе координат
 .
.
Тогда вектор напряженности  поля
поля  .
.
Для электрических полей, обладающих центральной или осевой симметрией (в сферической системе координат, где отсутствует зависимость от углов  и
и  ),
),
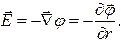
Таким образом силовая и энергетическая характеристики электрического поля связаны между собой соотношением (2.10): напряженность электростатического поля  равна градиенту потенциала со знаком "–". Знак "–" определяется тем, что вектор напряженности поля направлен в сторону убывания потенциала.
равна градиенту потенциала со знаком "–". Знак "–" определяется тем, что вектор напряженности поля направлен в сторону убывания потенциала.
Для графического изображения энергетической обстановки в электростатическом поле используются эквипотенциальные поверхности – поверхности, во всех точках которых потенциал  имеет одно и тоже значение. Так как между
имеет одно и тоже значение. Так как между  и
и  существует определенная взаимосвязь (2.10), то и во взаимном расположении элементов графического изображения силовой и энергетической обстановки в электростатическом поле (линий напряжённости и эквипотенциальных поверхностей) должна быть определенная закономерность.
существует определенная взаимосвязь (2.10), то и во взаимном расположении элементов графического изображения силовой и энергетической обстановки в электростатическом поле (линий напряжённости и эквипотенциальных поверхностей) должна быть определенная закономерность.
Рассмотрим элементарную работу по перемещению заряда Q вдоль эквипотенциальной поверхности на расстояние dx. Согласно (2.9)  , так как (
, так как ( ). В соответствии с формулой механической работы эта же работа dA равна
). В соответствии с формулой механической работы эта же работа dA равна

Ни одна из величин Q, E, dx не равна нулю, и для выполнения этого равенства необходима реализация условия  , то есть вектор
, то есть вектор  должен быть перпендикулярен dx (касательной к эквипотенциальной поверхности). Таким образом, линии напряженности всегда нормальны к эквипотенциальным поверхностям.
должен быть перпендикулярен dx (касательной к эквипотенциальной поверхности). Таким образом, линии напряженности всегда нормальны к эквипотенциальным поверхностям.
В любом электростатическом поле можно провести бесчисленное множество эквипотенциальных поверхностей (так же как и силовых линий). Обычно их проводят так, чтобы разности потенциалов между двумя соседними поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках (где эти поверхности расположены гуще – напряженность поля больше).
В качестве примера на рис. 2.2 показано взаимное расположение линий вектора  и эквипотенциальных поверхностей для поля двух равномерно заряженных параллельных плоскостей ("а") и поля точечного заряда ("б").
и эквипотенциальных поверхностей для поля двух равномерно заряженных параллельных плоскостей ("а") и поля точечного заряда ("б").


Рис. 2.2
Существующая взаимосвязь между напряженностью поля и потенциалом (2.10) позволяет по известной напряжённости поля находить разность потенциалов между двумя произвольными точками этого поля. В качестве примера рассмотрим поле равномерно заряженной бесконечной плоскости, напряженность которой определяется выражением (1.13) 
где  – поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х 1 и х 2 от плоскости согласно (2.9) равна
– поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х 1 и х 2 от плоскости согласно (2.9) равна
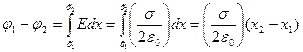 , (2.11)
, (2.11)
Аналогично, используя выражение (1.13а) для поля двух бесконечных параллельных разноименно заряженных плоскостей (расстояние между которыми " d "), получим, что разность потенциалов между плоскостями равна
 . (2.11а)
. (2.11а)
Локальное описание электростатических полей
Для локального описания электростатических полей в данной точке поля Р вводят следующие характеристики поля, полученные из усредненных величин: это дивергенция вектора  (
( ) и ротор вектора
) и ротор вектора  (
( ).
).
Дивергенцией (или расхождением) вектора  называют предел, к которому стремиться отношение потока ФЕ вектора
называют предел, к которому стремиться отношение потока ФЕ вектора  через замкнутую поверхность S к величине объема V, ограниченного этой поверхностью, когда объем V стремиться к нулю, а поверхность S стягивается к данной точке поля Р, т.е.
через замкнутую поверхность S к величине объема V, ограниченного этой поверхностью, когда объем V стремиться к нулю, а поверхность S стягивается к данной точке поля Р, т.е.
 .
.
Используя оператор Гамильтона 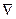 ,
,  можно записать как скалярное произведение
можно записать как скалярное произведение 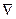 на
на  , и в декартовой системе координат
, и в декартовой системе координат  .
.
С помощью теоремы Гаусса ( ) можно доказать, что
) можно доказать, что  связана с объемной плотностью заряда
связана с объемной плотностью заряда 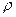 в данной точке поля следующим соотношением:
в данной точке поля следующим соотношением:  .
.
Это равенство является теоремой Гаусса в локальной или дифференциальной форме и показывает, что источниками электрического поля являются заряды.
Проекция ротора напряженности  (
( ) и в направлении положительной нормали
) и в направлении положительной нормали  равна пределу, к которому стремиться отношение циркуляции
равна пределу, к которому стремиться отношение циркуляции  по замкнутому контуру l к площади S, охватываемой этим контуром l. Когда площадь S стремиться к нулю, а контур l стягивается в точку, тогда
по замкнутому контуру l к площади S, охватываемой этим контуром l. Когда площадь S стремиться к нулю, а контур l стягивается в точку, тогда  , где n – нормаль к плоскости контура l, вдоль которой достигает максимума (
, где n – нормаль к плоскости контура l, вдоль которой достигает максимума ( ).
).
Используя дифференциальный оператор 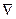 ,
,  записывается как векторное произведение
записывается как векторное произведение 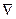 на
на  , и в декартовой системе координат равняется
, и в декартовой системе координат равняется  .
.
Из равенства нулю циркуляции вектора 

можно показать, что  в каждой точке электростатического поля и поле
в каждой точке электростатического поля и поле  является потенциальным.
является потенциальным.
Рассмотренные выше характеристики электростатического поля и закономерности в их взаимозависимости относились в основном к полю в вакууме. Естественно, что электростатическое поле в веществе имеет свою специфику. Посмотрим, как влияют особенности строения различных веществ на характеристики электростатического поля.
К началу