Если плоская кривая задана функцией  , то уравнения касательной и нормали в точке
, то уравнения касательной и нормали в точке  имеют вид:
имеют вид:
Уравнение касательной к кривой:  .
.
Уравнение нормали к кривой:  .
.
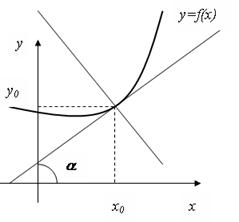
Рис. 13
Замечание: направление кривой в каждой ее точке определяется направлением касательной в этой точке.
|
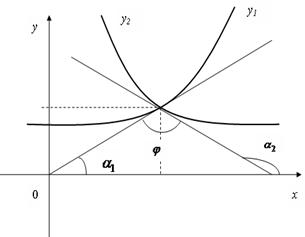
| Рис.14 |
Угол между пересекающими кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (Рис. 14) по формуле 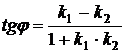 , где
, где  и
и 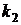 - угловые коэффициенты касательных к кривым в точке их пересечения
- угловые коэффициенты касательных к кривым в точке их пересечения  , т.е. частные значения в точке
, т.е. частные значения в точке  производных от y по x из уравнений этих
производных от y по x из уравнений этих
кривых:  ,
,  .
.
Пример 6. Найти уравнения касательной и нормали к кривой в заданной точке:
а)  при
при  .
.
Решение. Из уравнения кривой найдем  и производную
и производную 

 .
.
Уравнение касательной: 

 .
.
Уравнение нормали: 

 .
.
б)  в точке
в точке  .
.
Решение. Из уравнения кривой найдём производную:  , т.е.
, т.е. 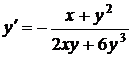 .
.
Следовательно,  .
.
Уравнение касательной: 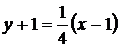 или
или  .
.
Уравнение нормали:  или
или  .
.
в)  при
при  .
.
Решение. Найдём  ,
,  и
и  . Следовательно
. Следовательно  .
.
Уравнение касательной:  или
или  .
.
Уравнение нормали:  или
или  .
.
Пример 7. Найти угол между параболами  и
и  .
.
Решение. Решив совместно уравнения парабол, находим точки их пересечения 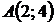 и
и  . Продифференцируем уравнения парабол:
. Продифференцируем уравнения парабол:  ,
,  . Найдём угловые коэффициенты касательных к параболам в точке А (т.е. значения производных при х =2):
. Найдём угловые коэффициенты касательных к параболам в точке А (т.е. значения производных при х =2): 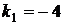 ,
,  . Следовательно,
. Следовательно,  ,
,  . Так же определяется угол между кривыми в точке В:
. Так же определяется угол между кривыми в точке В: 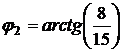 .
.
Исследование функций
Теорема 1. Если функция f (x) имеет производную на отрезке [ a, b ] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢ (x) ³ 0.
Теорема 2. Если функция f (x)непрерывна на отрезке [ a, b ] и дифференцируема на промежутке (а, b), причем f¢ (x) > 0 для a < x < b, то эта функция возрастает на отрезке [ a, b ].
Аналогично можно сделать вывод о том, что если функция f (x) убывает на отрезке [ a, b ], то f¢ (x)£0 на этом отрезке. Если f¢ (x)<0 в промежутке (a, b), то f (x) убывает на отрезке [ a, b ].
Функция f (x) имеет в точке  максимум, если
максимум, если  при любом D х [5].
при любом D х [5].
Функция f (x) имеет в точке  минимум, если
минимум, если  при любом D х.
при любом D х.
Точки максимума и минимума функции называются точками экстремума.
Замечание. Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Теорема 3 (необходимое условие существования экстремума) Если функция f (x) дифференцируема в точке  и точка
и точка  является точкой экстремума, то производная функции обращается в нуль в этой точке.
является точкой экстремума, то производная функции обращается в нуль в этой точке.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум.
Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно. Например.
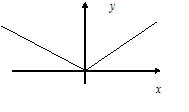
а) 
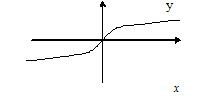
| б) 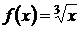
|
| 
|
В точке 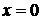 функция имеет минимум, но не имеет производной функция имеет минимум, но не имеет производной
| В точке 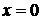 функция не имеет точек экстремума и не имеет производной функция не имеет точек экстремума и не имеет производной
|
Если при переходе через критическую точку не происходит изменение характера монотонности, то точка  не является точкой экстремума.
не является точкой экстремума.

| ||||||
| а) | б) | в) | г) | д) | ж) | з) |
| Рис. 15 |
На рис. 7 приведены возможные случаи, которые могут быть в критических точках (пусть  ):
):
а)  ,
,  ,
, 

 - точка максимума;
- точка максимума;
б)  ,
, 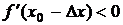 ,
, 

 - точка минимума;
- точка минимума;
в)  не существует,
не существует,  ,
, 

 -точка максимума;
-точка максимума;
г)  не существует,
не существует, 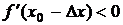 ,
, 

 - точка минимума;
- точка минимума;
д)  не существует,
не существует,  ,
, 

 - экстремума нет;
- экстремума нет;
е)  не существует,
не существует, 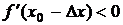 ,
, 

 - экстремума нет;
- экстремума нет;
ж)  ,
,  ,
, 

 - экстремума нет.
- экстремума нет.
Теорема 4 (достаточные условия существования экстремума). Пусть функция f (x) непрерывна в интервале (a, b), который содержит критическую точку  , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки
, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки  ).
).
Если при переходе через точку  слева направо производная функции f¢ (x) меняет знак с «+» на «-», то в точке
слева направо производная функции f¢ (x) меняет знак с «+» на «-», то в точке  функция f (x) имеет максимум, а если производная меняет знак с «-» на «+»- то функция имеет минимум.
функция f (x) имеет максимум, а если производная меняет знак с «-» на «+»- то функция имеет минимум.
На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции.
2) Найти значения функции в критических точках.
3) Найти значения функции на концах отрезка.
4) Выбрать среди полученных значений наибольшее и наименьшее.
Пусть в точке 
 и
и  существует и непрерывна в некоторой окрестности точки
существует и непрерывна в некоторой окрестности точки  .
.
Теорема 5. Если  , то функция f(x) в точке
, то функция f(x) в точке  имеет максимум, если
имеет максимум, если  и минимум, если
и минимум, если  .
.
Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
Теорема 6. Если во всех точках интервала (a, b) вторая производная функции 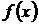 отрицательна, то кривая
отрицательна, то кривая 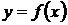 обращена выпуклостью вверх (выпукла).
обращена выпуклостью вверх (выпукла).
Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Теорема 7. Пусть кривая определяется уравнением 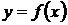 . Если вторая производная
. Если вторая производная 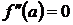 или
или 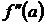 не существует и при переходе через точку
не существует и при переходе через точку 
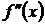 меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой  является точкой перегиба.
является точкой перегиба.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Из определения асимптоты следует, что если  или
или  или
или  , то прямая
, то прямая  – асимптота кривой y = f(x).
– асимптота кривой y = f(x).
Наклонная асимптота находится по формуле  , где
, где  ,
,  .
.
Замечание. Горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо:
1. найти область определения и область значений функции;
2. установить, является ли функция чётной или нечётной, периодической или нет;
3. исследовать поведение функции на  ;
;
4. найти точки разрыва функции и её односторонние пределы в этих точках;
5. найти точки пересечения графика функции с осями координат и интервалы знакопостоянства;
6. найти асимптоты графика функции;
7. найти точки экстремума и интервалы возрастания, убывания функции;
8. найти точки перегиба и интервалы выпуклости, вогнутости функции;
9. построить график функции, используя все полученные результаты исследования, если их окажется недостаточно, то следует найти ещё несколько точек графика функции, исходя из её уравнения.
Пример 8. Исследуем функцию  и построим её график.
и построим её график.
1) Заметим, что знаменатель имеет корни 1 и 2, так что функцию можно представить в виде 
Теперь легко видеть, что области определения функции не принадлежат только точки 1 и 2: D (f)=(-¥;1)È(1;2)È(2;+¥).
Область значений E (f) найти без всяких вычислений мы не можем; отложим этот вопрос до нахождения локальных экстремумов.
2) Поскольку область определения D (f) не симметрична относительно точки 0, функция не может быть ни чётной, ни нечётной. Очевидно также, что она не периодична (хотя бы потому, что её область определения не имеет периодической структуры).
3)  .
.
4) Область определения этой элементарной функции имеет две граничных точки: 1 и 2.
В достаточно малой левой окрестности точки 1  . А правый предел равен
. А правый предел равен 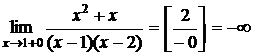
 в точке
в точке  разрыв второго рода.
разрыв второго рода.
Левый предел в точке x =2  , а правый
, а правый 
 в точке
в точке  разрыв второго рода.
разрыв второго рода.
5) Найдём точки пересечения графика с осями координат. Поскольку  , то график пересекает ось Oy (и, одновременно, ось Ox) в начале координат.
, то график пересекает ось Oy (и, одновременно, ось Ox) в начале координат.
Приравнивая числитель к нулю, получаем уравнение  , которое имеет два корня: x= 0 и x= -1. Значит, график пересекает ось Ox в этих двух точках (одну из них мы уже отметили ранее).
, которое имеет два корня: x= 0 и x= -1. Значит, график пересекает ось Ox в этих двух точках (одну из них мы уже отметили ранее).
Пользуясь методом интервалов (известным из школьной программы), определим знак функции на интервалах между корнями и точками разрыва (Рис.16). Таких интервалов получается пять: (-¥;-1);(-1;0);(0;1);(1;2);(2;+¥).


Рис. 16
Интервалы знакопостоянства[6] функции.
6)  . Значит, вертикальная прямая x =1 - это вертикальная асимптота графика функции.
. Значит, вертикальная прямая x =1 - это вертикальная асимптота графика функции.  Тем самым доказали, что вертикальная прямая x =2 служит второй вертикальной асимптотой графика функции.
Тем самым доказали, что вертикальная прямая x =2 служит второй вертикальной асимптотой графика функции.
Наклонная асимптота находится по формуле  , где
, где 
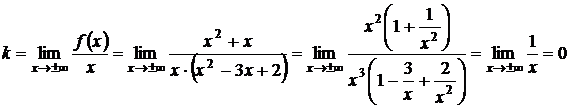 , а
, а 
 y =1 – прямая, которая служит горизонтальной асимптотой графика как при x®-¥, так и при x®+¥.
y =1 – прямая, которая служит горизонтальной асимптотой графика как при x®-¥, так и при x®+¥.
7) Найдём производную: 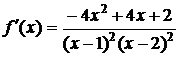 .
.
Для нахождения интервалов возрастания решим неравенство 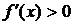 , эквивалентное квадратному неравенству
, эквивалентное квадратному неравенству  (при
(при 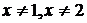 ), поскольку знаменатель принимает положительные значения. Решением квадратного неравенства служит интервал
), поскольку знаменатель принимает положительные значения. Решением квадратного неравенства служит интервал  ; однако точка x=1, не входящая в область определения, принадлежит этому интервалу. Тем самым, интервалов возрастания функции два: это
; однако точка x=1, не входящая в область определения, принадлежит этому интервалу. Тем самым, интервалов возрастания функции два: это 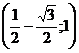 и
и 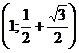 .
.
Для нахождения интервалов убывания нужно решить неравенство  , или (
, или ( при
при 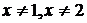 ). Решением квадратного неравенства служит, очевидно, объединение двух интервалов
). Решением квадратного неравенства служит, очевидно, объединение двух интервалов  и
и  ; точка x=2 делит второй из них на две части.
; точка x=2 делит второй из них на две части.
Тем самым, функция убывает на трёх интервалах (Рис. 17):  , и
, и 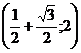 , (2;+¥).
, (2;+¥).

Рис. 17
Точка  является точкой минимума,
является точкой минимума, 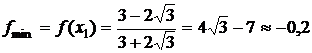 . Точка
. Точка  является точкой максимума,
является точкой максимума,  .
.
Теперь мы можем записать область значений функции:
это E (f)=(-¥; f max]È[ f min;+¥)»(-¥;-13,8]È[-0,2;+¥).
8) Найдём вторую производную:  .
.
Для нахождения интервалов выпуклости, вогнутости нужно решить неравенство  . Заметим, что числитель
. Заметим, что числитель  меняет знак при переходе через точку. x 0»-0,919.Поскольку знаменатель содержит нечётные степени биномов x -1 и x -2, то они также меняют знак при переходе, соответственно, через точки x =1 и x =2. Итак,
меняет знак при переходе через точку. x 0»-0,919.Поскольку знаменатель содержит нечётные степени биномов x -1 и x -2, то они также меняют знак при переходе, соответственно, через точки x =1 и x =2. Итак,  меняет знак при переходе через три точки: x 0, 1 и 2. Из этих трёх точек функция f (x) непрерывна только в точке x 0, так что это единственная точка перегиба. Методом интервалов легко выясняем, что на интервалах (-¥; x 0) и (1;2) функция выпукла, а на интервалах (x 0 ;1) и (2;+ ¥) – вогнута (Рис. 18).
меняет знак при переходе через три точки: x 0, 1 и 2. Из этих трёх точек функция f (x) непрерывна только в точке x 0, так что это единственная точка перегиба. Методом интервалов легко выясняем, что на интервалах (-¥; x 0) и (1;2) функция выпукла, а на интервалах (x 0 ;1) и (2;+ ¥) – вогнута (Рис. 18).

Рис. 18
Интервалы выпуклости, вогнутости
9) С учётом предыдущих семи пунктов строим график функции (Рис. 19).

Рис. 19