1. Приближенное моделирование
В курсе ставится целью создание практически приемлемых приемов расчета на прочность и жесткость типовых строительных и машиностроительных элементов конструкций. Для этого широко используются упрощающие гипотезы и приближенные методы расчетов.
Упрощающие гипотезы – предположения о характере нагрузок, деформаций, свойств материала. В результате полученная математическая модель – обычно система дифференциальных уравнений – получается достаточно сложной и часто не допускает аналитического решения. Извлечение практической информации из математической модели в этом случае производится приближенно:
- численными методами,
- упрощением самой модели,
- выделением частных случаев, имеющих аналитическое решение, и распространением результатов на общее решение (суммированием результатов простых воздействий).
В результате приближенного моделирования и приближенных расчетов оценка напряженного (НС) и деформированного (ДС) состояний также приближенна. Адекватность расчетов обеспечивается сравнением с результатами специальных экспериментов, расчеты по которым проводятся с теми же упрощающими гипотезами, что и моделирование НС и ДС с некоторым запасом (см. выше). Такой подход хорошо разработан и дает удовлетворительные результаты для типовых элементов (подробно в разделе детали машин). В других случаях после расчета и проектирования необходимы длительные натурные испытания и доводка опытных экземпляров машин и конструкций.
Упрощающие гипотезы применяются на разных этапах моделирования и вместе представляют собой систему схематизации объекта и его свойств. Рассмотрим основные этапы схематизации при моделировании НС и ДС, принятые в курсе.
2. Напряженное состояние и гипотезы прочности
НС в теле определяется как совокупность нормальных и касательных напряжений во всех плоскостях и точках тела. Рассмотрим численную оценку НС и предельные значения этой оценки с точки зрения прочности.
Введем правую декартову систему координат, связанную с ненагруженным телом, и опишем в ней напряжения на бесконечно малой площадке в точке.
Сначала выберем площадку, перпендикулярную одной из координатных осей, например ox. Касательное напряжение разложим по координатным осям. Составляющие полного напряжения обозначим 
. Первый индекс всегда означает направление нормали к площадке, а второй – какой оси параллельна составляющая полного напряжения. При повторяющихся индексах второй опускается.
При выборе площадок перпендикулярно другим координатным осям получим 
.
Покажем, что знание девяти чисел – проекций полных напряжений на три взаимно перпендикулярных площадки – достаточно для вычисления напряжений на произвольной площадке.
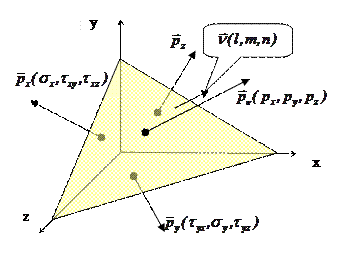Выделим в точке элементарный тетраэдр, одна грань которого - произвольная площадка, а три других – координатные площадки. Положение произвольной площадки 
будем задавать ортом нормали с проекциями 
- 
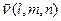. В сопротивлении материалов эти проекции называют направляющими косинусами, так как они численно равны косинусам углов наклона нормали к площадке к осям координат. Очевидно, что
. *
Составляющие вектора напряжений на произвольной площадке в проекциях на координатные оси обозначим 
, т.е.
.
Тетраэдр находится в равновесии, как и все тело в целом. Обозначим площадь наклонной грани dA, тогда площади координатных граней как проекций наклонной площади
.
Орты нормалей координатных граней противоположны координатным осям. Условие равновесия сил, действующих на элементарный тетраэдр в векторном виде:
В проекциях на координатные оси, после сокращения на dA, получаем три уравнения:
,
, **
.
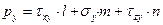Рассматривая равновесие моментов относительно координатных осей (вывод опускаем для экономии времени, предлагается сделать самим), получаем:
.
Полученные соотношения в сопротивлении материалов называют
законом парности касательных напряжений.
Таким образом, НС в точке (напряжения на любой площадке, проходящей через точку) описывается шестью числами – тремя нормальными 
и тремя касательными 
напряжениями на координатных площадках. Количество параметров можно вдвое уменьшить, если выбрать координаты в точке так чтобы в координатных площадках отсутствовали касательные напряжения. Такие площадки называют главными.
Систему ** можно представить на как линейное преобразование вектора 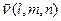в вектор 
с симметричной матрицей преобразования
,
а именно
.
Такое преобразование имеет три взаимно перпендикулярных собственных вектора 
, преобразование которых сводится к умножению на скаляр – одно из собственных чисел 
матрицы 
. Собственные вектора образуют новую систему координат (главные оси напряжений), в которой отсутствуют касательные напряжения, а нормальные напряжения - главные напряжения 
- вычисляются как собственные числа матрицы - корни кубического уравнения
.
В развернутом виде
где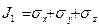 
, 
, 
.
В главных осях ** принимает вид
. ***
Нормальное напряжение на произвольной площадке (повернутой относительно главных осей)
или в развернутом виде
. ****
Полное напряжение – векторная сумма нормального и касательного напряжений, т.е
. *****
Система (*,****,*****), линейная относительно квадратов проекций нормали, исследовалась Мором на положительные корни. Графическая интерпретация результатов представлена на рисунке – круги Мора. Вывод предлагается изучить самостоятельно. Суть его в том, что решение системы должно давать положительные корни (квадраты косинусов). Круги Мора соответствуют условиям
Возможные комбинации нормальных и касательных напряжений на произвольной площадке включают только заштрихованную область. Если обозначить главные напряжения так, что
,
то
,
.
Таким образом, напряженное состояние количественно описывается тремя числами – главными напряжениями.
Рассматриваются три частных случая НСТ:
- линейное напряженное состояние, когда два из трех главных напряжений два равны нулю,
- плоское напряженное состояние, когда одно из главных напряжений равно нулю,
- чистый сдвиг, когда при плоском НС два главных напряжения равны по модулю и противоположны по знаку (из кругов Мора следует, что в точке существуют две противоположные площадки, в которых отсутствуют нормальные напряжения, а касательные равны по модулю главным напряжениям.).
Линейное НС реализуется при растяжении стандартного образца, т.к. в поперечных сечениях отсутствуют касательные напряжения, а в продольных сечениях вообще отсутствуют напряжения.
 | |||||||||
 | |||||||||
 | |||||||||
| |||||||||
| |||||||||
Плоское НС всегда наблюдается на ненагруженной поверхности детали, так как в плоскости, совпадающей с поверхностью, нет никаких напряжений.
Чистый сдвиг примерно реализуется при кручении тонкостенного трубчатого образца моментом Мz (подробно см. ниже при решении задачи о кручении круглого стержня).
Как уже говорилось, опасность напряженного состояния оценивается гипотезами (предположениями) Их известно более ста. Рассмотрим три наиболее применяемые.
· Напряженные состояния равноопасны, если равны максимальные касательные напряжения (гипотеза 3).
При растяжении стандартного образца очевидно 
и максимальное касательное напряжение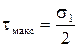 
. Разрушение происходит при 
, (т.е. при 
). Тогда в общем случае нагружения разрушение произойдет при 
или 
. Напряженное состояние, эквивалентное растяжению, характеризуется числом
,
а условие прочности
.
· Напряженные состояния равноопасны, если равны удельные потенциальные энергии изменения формы (гипотеза 4, пока без вывода).
Напряженное состояние, эквивалентное растяжению, характеризуется числом
.
Гипотезы дают разницу в пределах разброса механических характеристик материала. Например, при определении 
при кручении (чистый сдвиг 
) 
, а 
. Средняя разница в теориях составляет 
. В других напряженных состояниях разница меньше и стремится к нулю. Обычный разброс результатов испытаний на растяжение составляет 
и может достигать в двух опытах 14%. Т.е. достоверность гипотезы практически не удается оценить. В то же время погрешность расчета по одной из рассмотренных гипотез надежно перекрывается принятыми запасами прочности. Рассмотренные две гипотезы практически равносильны для сталей.
Для материалов с разной прочностью сжатия и растяжения принята третья гипотеза (гипотеза 5 Мора)
,
где коэффициент 
равен отношению прочности растяжении к прочности при сжатии. Для бетона 
(см. лек. 1), для металлов практически 
.
Задача расчета на прочность состоит в определении максимальных эквивалентных напряжений в теле по принятой гипотезе и сравнении их с допускаемыми из опыта на растяжение.
3. Реальный объект и расчетная схема
Учесть в расчетах все реально влияющие на прочность и жесткость факторы практически невозможно. Поэтому исследование начинается с выбора расчетной схемы, т.е. необходимо провести схематизацию объекта и отбросить все те факторы, которые не могут существенно повлиять на работу. Степень упрощения расчетной модели в конкретных случаях решается на этапе проектирования и уточняется при испытаниях и эксплуатации. Для типовых деталей расчетные схемы хорошо отработаны и практически не требуют экспериментальной проверки. При существенном изменении конструкции появляется необходимость испытаний по доводке. В ответственных случаях (например, в авиации, автомобилестроении) доводка изделия и уточнение расчетных схем продолжаются и при эксплуатации. При этом на начальном этапе эксплуатации принимаются меры по ограничению эксплуатационных нагрузок.
Рассмотрим в качестве примера расчетную схему каната лифта.
При малой высоте подъема тихоходных лифтов основной фактор нагрузки – сила Р от веса лифта.
При большой высоте подъема следует учитывать действие собственного веса троса (удельный вес материала γ, площадь сечения А), т.е. добавить в расчетную схему распределенную по длине троса (погонную) нагрузку q= γ·A.
Для быстроходных лифтов (ускорение лифта α, ускорение свободного падения g, масса лифта Р/g) следует учесть силу инерции лифта, т.е. прибавить к его весу 
.
Другими факторами – силой инерции троса, гидродинамическим сопротивлением воздуха, переменностью температуры по длине троса можно пренебречь.
Обобщим расчетную схему растяжения (сжатия) стержня – длинного призматического тела.
Стержень длиной l может быть нагружен несколькими сосредоточенными силами Рi и погонными нагрузками qi. Координаты приложения нагрузок будем отсчитывать от левого конца. Опоры могут быть приняты условно неподвижными и подвижными. Если деформации стержня от рабочих нагрузок соизмеримы с деформациями опоры, то опора считается упругой с жесткостью С.
Аналогичная расчетная схема стержня при изгибе. На рисунке пример расчетной схемы балки – горизонтального изгибаемого элемента конструкций.