 Применение при математическом моделировании аппарата бесконечно малых приводит к необходимости считать материал однородной и сплошной средой. В противном случае необходимо применять дискретную математику, что необозримо усложняет математическое описание и расчеты. По этой же причине приходится считать материал изотропным – свойства материала одинаковы во всех направлениях. Ясно, что последнее приемлемо для металлов, и является существенным упрощением для дерева и композитных материалов.
Применение при математическом моделировании аппарата бесконечно малых приводит к необходимости считать материал однородной и сплошной средой. В противном случае необходимо применять дискретную математику, что необозримо усложняет математическое описание и расчеты. По этой же причине приходится считать материал изотропным – свойства материала одинаковы во всех направлениях. Ясно, что последнее приемлемо для металлов, и является существенным упрощением для дерева и композитных материалов.
Математические проблемы приводят также к необходимости считать материал идеально и линейно упругим. При этом мы получаем линейные уравнения, решение которых существенно проще нелинейных, а также принцип независимости действия сил. Последний говорит, что порядок приложения сил не влияет на конечный результат, что существенно упрощает расчеты на прочность и жесткость.
На рисунке приведен пример диаграммы растяжения образца длиной l из углеродистой стали (подробнее смотри лабораторную работу №9 в лабораторном практикуме по СМ). Будет показано, что при первом нагружении нагрузка идет по диаграмме растяжения, а разгрузка по закону Гука. Пусть сила Р1 приводит в напряжениям в пределах закона Гука, а сила Р2 - за пределами закона Гука. Прикладывая силы в порядке Р1 – Р2 получаем удлинение Δl1 , изменяя порядок на Р2 – Р1 – Δl2 . Таким образом принцип независимости действия сил не выполняется. Уменьшая Р2 и оставаясь в пределах упругости сохраняем принцип независимости действия сил.
В большинстве расчетов выход за пределы упругости не допустим.
1.Линейная деформация даже для сталей  и приводит к значительным изменениям размеров детали в процессе эксплуатации - выходу за пределы допустимых нагрузок (по второй группе предельных состояний).
и приводит к значительным изменениям размеров детали в процессе эксплуатации - выходу за пределы допустимых нагрузок (по второй группе предельных состояний).
В машиностроении это приводит к нарушению условий сопряжения деталей, в строительстве – к большим прогибам.
2. Не возвращение детали к начальным размерам после нагрузки означает, что часть энергии, затраченной на деформацию, переходит в материал, необратимо меняя его свойства, накапливается при циклическом нагружении приводит к его усталости. Последний факт знаком всем : порвать проволоку руками не хватает сил, а многократный ее изгиб при больших деформациях быстро приводит к разрушению. В практических расчетах это выход нагрузок за пределы третьей группы предельных состояний (определяется образованием и развитием трещин и других повреждений).
Все сказанное приводит к применению в большинстве расчетах линейной зависимости между напряжениями и деформациями. При растяжении образца деформация постоянна и это
 ,
,
где 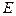 - модуль нормальной упругости материала (модуль Юнга),
- модуль нормальной упругости материала (модуль Юнга), 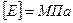 :
:
для сталей 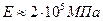 ,
,
для алюминиевых сплавов  ,
,
для сплавов титана  ,
,
для бетона 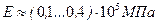 .
.
В поперечных площадках деформация меняет знак и
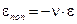 .
.
Коэффициент поперечной деформации (коэффициент Пуассона) 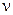 безразмерный и составляет:
безразмерный и составляет:
для сталей 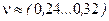 ,
,
для алюминиевых сплавов 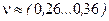 ,
,
для бетона 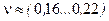 .
.
(Подробнее смотри лабораторную работу №1 в лабораторном практикуме по СМ. Там же излагается метод определения деформаций).
5. Схематизация формы детали
Решение задачи расчета на прочность и жесткость для тела произвольной формы аналитически невозможно. Численное решение громоздко, требует специальных навыков и неудобно при проектировании. Для упрощения задачи проводится схематизация формы тела: стержень, пластина, оболочка.
Стержень – тело, один из размеров которого существенно (на порядок и больше) больше двух других. Пластина – плоская деталь, один из размеров которого существенно меньше двух других. Оболочка – неплоская деталь, один из размеров которого существенно меньше двух других.
Пример: у ведра дужка – стержень, дно – пластина, боковая поверхность – оболочка.
Конечно, реальные конструкции не всегда подходят под принятую схематизацию. В этом случае схема принимается приближенно. Например, вал считают стержнем, а он бывает коротким. Расчеты поправляются специальными коэффициентами. В частности, в деталях машин вводятся специальные допускаемые напряжения для валов из данного материала. В некоторых случаях деталь разбивается на элементы, подходящие под схематизацию. Например – телевизионная вышка – стержневая система.
6. Схематизация сил. Принцип Сен-Венана
Очевидно, что понятие сосредоточенная сила в принципе не применимо в СМ, так как сила в точке дает бесконечные напряжения. Реально имеет место некоторая контактная площадка и напряжения не бесконечны. Поэтому правильно ограничиться понятиями вектора  поверхностных сил с размерностью давления и вектора
поверхностных сил с размерностью давления и вектора 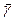 объемных сил (силы инерции, силы внешних полей, собственный вес) с размерностью удельного веса. Для стержней эти силы приводят к оси и называют погонными с размерностью Н/м или Н/мм.
объемных сил (силы инерции, силы внешних полей, собственный вес) с размерностью удельного веса. Для стержней эти силы приводят к оси и называют погонными с размерностью Н/м или Н/мм.
Сложность заключается в правильном описании изменения сил по площади (попробуйте представить, как меняется давление одной детали на другую в пределах площадки контакта и размеры этой образующейся площадки). С другой стороны, очевидно, что за пределами контактной площадки результат нагружения не зависит от закона распределения сил по площадке (принцип Сен-Венана). Поэтому силы и моменты, действующие по относительно малым площадкам, можно считать сосредоточенными. Расчеты же контактных напряжений вести отдельно в случае необходимости. Например, зубчатые колеса считают отдельно на контактную, отдельно на изгибную прочность.
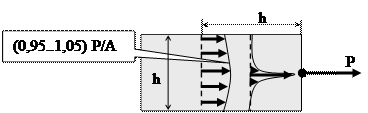 Точные численные расчеты хорошо иллюстрируют принцип Сен-Венана.
Точные численные расчеты хорошо иллюстрируют принцип Сен-Венана.
 Как видно из примера, на расстоянии порядка поперечного размера стержня напряжения от сосредоточенной силы распределены практически равномерно, т.е. допустимо применение принципа Сен-Венана.
Как видно из примера, на расстоянии порядка поперечного размера стержня напряжения от сосредоточенной силы распределены практически равномерно, т.е. допустимо применение принципа Сен-Венана.
7. Схематизация деформаций
Рассматривается в тесной связи со схематизацией формы детали.
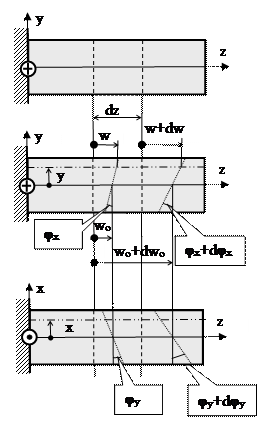
В стержнях поперечное сечение считается плоским после нагружения (гипотеза Бернулли). В пластинах и оболочках нормаль к срединной поверхности считается после нагружения прямой. Такие упрощения характера деформации существенно упрощают расчеты, уменьшая число параметров. Рассмотрим на примере изгиба и растяжения (сжатия) стержня. Задачу решаем в главных центральных осях.
Обозначим перемещение точек вдоль оси стержня w, перемещения точек оси wо, поворот сечения относительно оси x - φx, оси y – φy. Рассмотрим два бесконечно близких сечения на расстоянии dz.
Перемещение точки (волокна) с координатами x,y с учетом поворота сечения
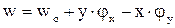 ,
,
а его дифференциал (приращение на отрезке оси dz)
 .
.
Линейная деформация
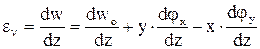 .
.
Закон Гука при растяжении волокна
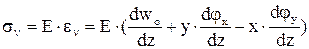 . Сравнивая с результатами приближенного представления функции
. Сравнивая с результатами приближенного представления функции  рядом, получаем, первые три члена ряда суть
рядом, получаем, первые три члена ряда суть
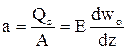 ,
, 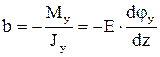 ,
,  .
.
Представление функции  первыми тремя членами ряда есть представление перемещений сечения как перемещение плоскости. Реально сечение, конечно, не плоское, и отклонения от плоскости описывается отброшенными членами ряда (это называется депланацией сечения).
первыми тремя членами ряда есть представление перемещений сечения как перемещение плоскости. Реально сечение, конечно, не плоское, и отклонения от плоскости описывается отброшенными членами ряда (это называется депланацией сечения).
Для перемещений сечения получаем разрешающие дифференциальные уравнения,
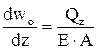 ,
,  ,
,  ,
,
из которых видно влияние площади сечения и главных центральных моментов инерции на деформации.