КОЛОКВИУМ
1. Матрица и действия над ними. Нулевая, одиничная, треугольные матрицы. Матрица поворота на угол α. Запись через столбцы.
1) Матрицы – совокупность чисел расположенных в виде таблицы из m строк и n столбцов:
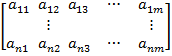
- элементы матрицы
i – индекс строки
j – индекс столбца
2) Действия:
Сумма матриц А и В одинаковых размеров, это матрица С, элементы которой 
= 
+ 
Произведением матрицы А на число α называется матрица С, элементы которой равны произведениям 
матрицы А на число α.
3) Нулевая матрица – матрица, все элементы которой равны нулю.
Единичная матрица – матрица, у которой все элементы главной диагонали равны единице, а все остальные элементы равны нулю.
Треугольная матрица – матрица, все элементы которой ниже(выше) диагонали равны нулю.
4) Матрица вида: 
– называется матрицей поворота на уголα ( 
)
5) Запись через столбцы:
если 
= 
, 
= 
, ……., 
= 
тогда матрицу 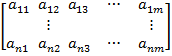можно записать в виде | 
, 
, …., 
|
2. Аксиомы линейного пространства. Линейная комбинация, зависимость и свойства системы столбцов. Базис евклидового пространства 
.
1) Аксиомы линейного пространства:
A+B=B+A
(A+B)+C=A+(B+C)
Α(A+B)=αA+αB
(α·β)A=α(β·A)
(α+β)A=αA+βA
2) Линейная комбинация:
Из матриц одинаковых размеров 
, ….., 
и чисел 
,….., 
мы можем составлять выражения вида: 
,,….., 
Такие выражения называются линейными комбинациями.
3) Линейная зависимость:
Система матриц , ….., линейно независима, если нулевая матрица раскладывается по ней однозначно, т.е. из 
,,…..,
следует 
=…..= =0. В противоположном случае, т.е. если существует k чисел ,….., одновременно не равных нулю, то система матриц линейно зависима.
4) Свойства системы столбцов:
|
|
1: Система столбцов линейно зависима, если хотя бы один из низ является линейной комбинацией остальных.
2: Если в систему входит столбец из нулей, то она линейно зависима.
3: Если имеется линейно зависимая подсистема, то содержащая ее система также линейно зависима.
4: из линейно независимой системы можно выделить линейно независимую подсистему.
Перестановки, инверсии, четность. Определитель n-го порядка. Правила вычисления определителя 2-го и 3-го порядков.
1) Перестановка – перестановка n различных чисел не превосходящих nзапись этих чисел в определенном порядке.
1, 2, 3, 4, …, n-1, n 2, 1, 3, 4, …, n-1, n
Инверсия – когда меньшее число стоит правее большего n, n-1, …., 4, 3, 2, 1.
Транспозиция – смена порядка следования чисел.
Четная или нечетная число беспорядков - четность
3, 2, 1, …, n-1, n – нечетная.
2) Определитель n-го порядка:
Есть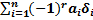 
где r – число беспорядков в δ.
Определитель 2-го порядка: detA= 
Определитель 3-го порядка: detA= 
Простейшие свойства (1-9) определителя матрицы.
1) Свойства определителя матрицы:
1: Определитель не изменяется при транспонировании: det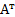 
=detA.
2: При перестановке строк (столбцов) определитель меняет знак.
3: Определитель с двумя одинаковыми строками (столбцами) равен нулю.
4: Определитель содержащий строку(столбец) из нулей равен нулю.
5: При умножений строки(столбца) на число, весь определитель умножается на это число.
6: Если строка(столбец) является суммой строк(столбцов), то определитель также раскладывается в сумму определителей.
7: При прибавлении к некоторой строке(столбцу) другую строку(столбец) определитель не меняется.
|
|
8: При прибавлении к некоторой строке(столбцу) линейную комбинацию других строк(столбцов) определитель не меняется.
9: detA= 