Сайт: Сhaplygynyy.narod.ru
Опубликовано: «Практическая силовая электроника», вып.25, 2007
Попков О.З, Чаплыгин Е.Е.
РАСЧЕТ ВЫПРЯМИТЕЛЕЙ С ЕМКОСТНЫМ ФИЛЬТРОМ
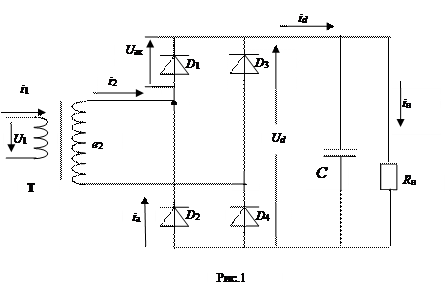Расчет однофазного выпрямителя. Анализируя процессы в двухполупериодном выпрямителе с С-фильтром (рис. 1а) пренебрегаем сопротивлением соединительных проводов, питающую сеть и диоды выпрямителя считаем идеальными.
На рис.2 приведены временные диаграммы напряжений и токов в характерных участках схемы.
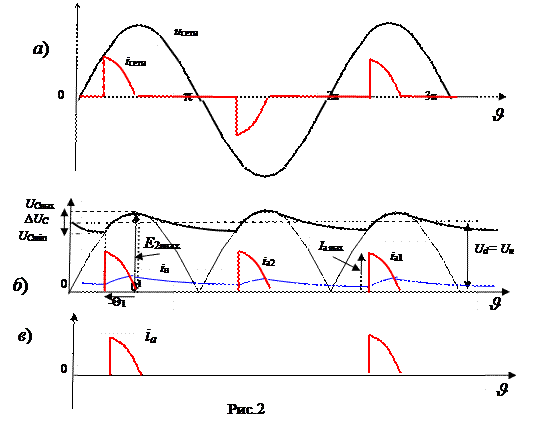
Коэффициент пульсации (q) пульсирующего напряжения часто определяется как отношение амплитуды первой гармоники переменной составляющей к среднему значению напряжения. Однако МЭК (термин 551-17-29) содержит и другое определение коэффициента пульсации: отношение половины изменения напряжения на конденсаторе D UC /2 (рис.1,а) к среднему значению напряжения на нагрузке Ud, или:
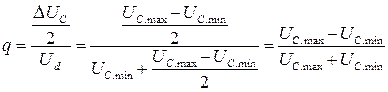(1)
Учитывая, что амплитуда напряжения на конденсаторе равна амплитуде напряжения 
и принимая во внимание (1), можно определить среднее напряжение и ток на выходе выпрямителя:
(учитывая, что по определению 
).
откуда:
(2)
при этом 
(3)
. 
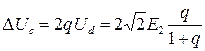(4)
Очевидно, что диод выпрямителя начинает пропускать ток в момент, когда мгновенное значение сетевого напряжения превысит величину напряжения на конденсаторе, определяемом углом отсечки q 1 (рис.2,а):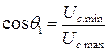 
. Из уравнения (1) 
Отсюда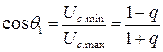 
;
Или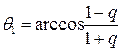 
(5)
Вентиль заканчивает пропускать ток при угле отсечки q 2, когда производная сетевого напряжения становится больше, чем производная от функции, определяющей разряд конденсатора. Ток конденсатора в этот момент равен по модулю току нагрузки. Начало отсчета углов отсечки соответствует максимальному значению сетевого (питающего) напряжения. Из условия равенства производных в момент q 2
;
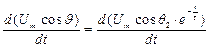откуда
,
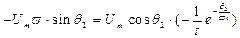выражаем угол отсечки q 2:
,
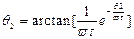где t = R н С. Учитывая, что для малых углов
,
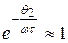получаем:
(6)
При малых значениях q (очевидно, что при больших значениях τ=R н C) угол ϴ 2 стремится к нулю.
Из временных диаграмм видно, что диод открывается в момент минимального напряжения на нагрузке:
.
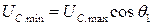С другой стороны процесс разряда конденсатора током нагрузки имеет экспоненциальный характер:
,
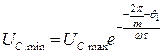где m = 2 – пульсность выпрямителя: количество пульсаций на стороне постоянного тока за период сети.
Приравниваем полученные два соотношения и учитывая, что: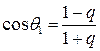 
.
После несложных преобразований имеем:
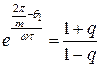
Прологарифмировав выражение с учетом того, что угол q 2 мал и cos q 2 » 1, окончательно получаем:
.
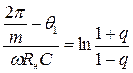Отсюда: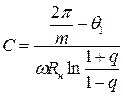 
(7)
На интервале проводящего состояния вентиля к конденсатору прикладывается напряжение источника питания, поэтому ток конденсатора:
Где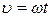 
Ток диода на интервале проводимости равен сумме токов нагрузки и конденсатора (рис.1,б):
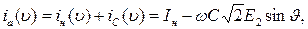(8)
Тогда максимальное значение анодного тока, достигаемое в момент - q 1, равно
(9)
Среднее значение тока вентиля:
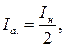(10)
Действующее значение анодного тока вторичной обмотки трансформатора:
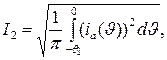. (11)
При расчетах можем пренебречь пульсациями тока нагрузки: i н = Id.
Действующее значение тока, протекающего через первичную обмотку трансформатора:
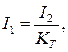. (12)
Несмотря на наличие ряда допущений точность расчета достаточно высока, как правило, она выше точности исходных данных и стабильности параметров компонентов.
соответствии с (12): IC = 5,08 A