Анализ неаризованной выводы

Задание 1.

По исходным данным выполните следующие задания:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнений линейной, степенной и показательной (экспоненциальной) парной регрессии.

3. Оцените тесноту связи с помощью показателей корреляции и де­терминации.

4. Оцените с помощью средней ошибки аппроксимации качество моделей регрессий.

5.Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования, с помощью t-статистики – значимость параметров регрессии (линейной и линеаризованной форм). По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

6. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α = 0,05.

7. Оцените полученные результаты для трех моделей, выводы оформите в аналитической записке.

8.

функция	Аналитическое выражение	R2	Теснота связи		F-критерий	t-статистика для параметров регрессии	Yпрогнозн, доверительный интервал

 

 

Исходные данные для моделирования по заданию 1

 

Вариант 1. По регионам Центрального федерального (без г. Москвы) и Уральского округов известны данные за 2013 г.

 

Район	Потребительские расходы на душу населения, руб., у	Денежные доходы на душу населения, руб., х
Белгородская область
Брянская область
Владимирская область
Воронежская область
Ивановская область
Калужская область
Костромская область
Курская область
Липецкая область
Московская область2)
Орловская область
Рязанская область
Смоленская область
Тамбовская область
Тверская область
Тульская область
Ярославская область
Курганская область
Свердловская область
Тюменская область
Челябинская область

 

Решение:

1. Построить поле корреляции

 

 

Гипотеза о форме связи: Связь прямая т. к. r_xy > 1 (положительное значение), тесная.

 

 

2. Рассчитайте параметры уравнений линейной, степенной и показательной (экспоненциальной) парной регрессии.

 

Рассчитаем параметры уравнений линейной парной регрессии:

 

1) С помощью мастера диаграмм Excel изобразим поле корреляции (зависимость y_i от x_i), выбрав тип диаграммы – ТОЧЕЧНАЯ.

 

 

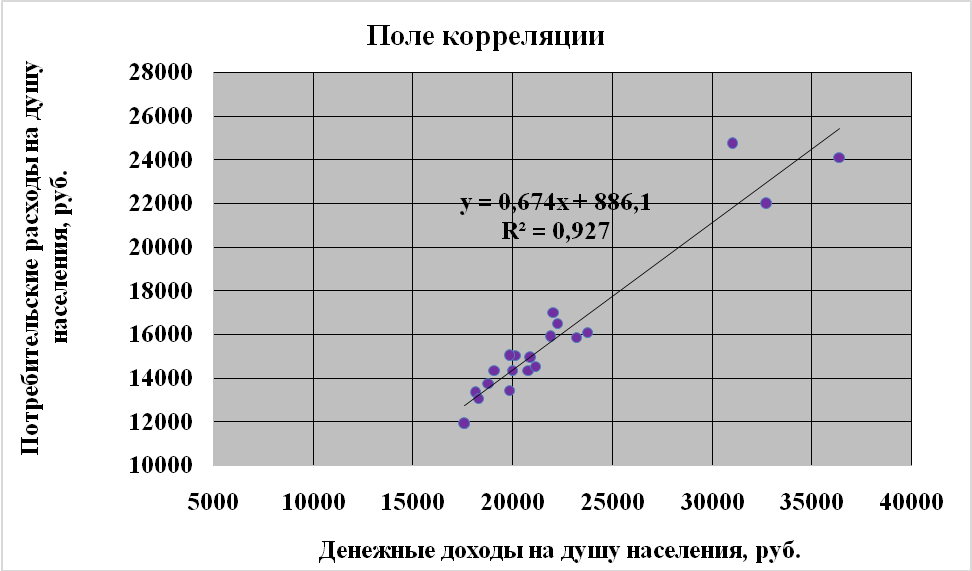
Линейное уравнение регрессии имеет вид.

2) Построим линию тренда линейного типа, которая Полученное уравнение вида: будет являться линейной регрессионной моделью зависимости потребительских расходов на душу населения и от уровня доходов населения на душу населения.

Линейное уравнение регрессии имеет вид .

 

3) Для оценки качества параметров регрессии построим расчетную таблицу

№ пп	Субъекты РФ	x i	y i	xi 2			|yi- |	|yi- |/ yi	(yi-)2	(-)2	(y i-)2
	Белгородская область					16 887,17	788,172	0,048957823		285176578,2	621215,1016
	Брянская область					14 471,68	569,317	0,037851007		209429608,9	324121,8465
	Владимирская область					13 557,53	207,468	0,015072139		183806673,9	43042,97102
	Воронежская область					15 755,27	1250,73	0,073546395		248228532,8	1564325,533
	Ивановская область					13 103,83	218,172	0,01637682		171710308,3	47599,02158
	Калужская область					16 514,37	638,365	0,040209436		272724251,4	407509,8732
	Костромская область					12 734,39	797,392	0,066800034		162164739,6	635834,0017
	Курская область					14 914,60	545,601	0,037970701			297680,4512
	Липецкая область					15 867,18	655,821	0,0396914		251767369,4	430101,184
	Московская область					22 957,24	977,242	0,04446051		527034960,2	955001,9266
	Орловская область					13 197,54	131,535	0,010066968		174174930,1	17301,45623
	Рязанская область					14 253,26	802,258	0,059643001		203155363,6	643617,8986
	Смоленская область					14 357,08	1,923	0,000133923			3,697929
	Тамбовская область					14 257,30	770,697	0,05128407		203270688,8	593973,8658
	Тверская область					13 766,52	590,48	0,041128369		189517072,9	348666,6304
	Тульская область					14 977,97	49,972	0,003347535		224339645,2	2497,200784
	Ярославская область					15 128,98	585,982	0,040293062		228886096,4	343374,9043
	Курская область					12 739,79	838,785	0,070480212		162302121,8	703560,2762
	Свердловская область					21 793,65	2942,346	0,118949951		474963354,7	8657399,984
	Тюменская область					25 424,64	1307,64	0,054220674		646412319,1	1709922,37
	Челябинская область					15 642,01	255,988	0,0161019		244672539,4	65529,85614
	Итого:					332 302,000	14925,886	0,886585929			18412280,05

4) Рассчитаем средние показатели x_i и y_i и сигму квадрат:

	Среднее значение	22157,80952	15823,90476
	Сигма квадрат	24516978,54	12019293,13

 

по формулам:

с помощью функции excel: СТАНДОТКЛОНП (C3:C23)^2 = 24516978,54

СТАНДОТКЛОНП(D3:D23)^2=12019293,13

5) Определим коэффициент детерминации для анализа общего качества уравнения линейной формы регрессии R².

, т.е. в 92,7% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии весьма высокая. Остальные 7,3% изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).

6) Средняя ошибка апросимации:

В среднем, расчетные значения отклоняются от фактических на 4,222%. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии.

7) Проверим значимость коэффициента корреляции.

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: 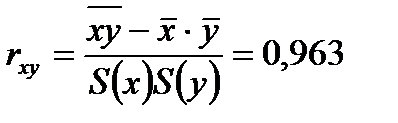, т.е. связь прямая и тесная.

8) Проверим значимость всего уравнения в целом по критерию Фишера.

Подсчитаем значение F_факт=241,4619054

Табличное значение критерия со степенями свободы:

k₁=1 и k₂=21, F_табл = 2,1438. (Для расчета критического значения использовали статистическую функцию = FРАСПОБР(0,05;21;21-1-1)

Выдвигаем гипотезы:

H₀: r_xy = 0, нет линейной взаимосвязи между переменными;

H₁: r_xy ≠ 0, есть линейная взаимосвязь между переменными;

Гипотеза H₀ – о том, что R²=0 (незначимости R²), отвергается, если F_факт>F_табл, т.е. гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

9) Определим стандартные значения ошибки σ_a, σ_b, для коэффициентов регрессии.

; ;

σ_a,= 3511,475334; σ_b,= 0,043384427

Гипотеза H₀ – о том, что коэффициенты регрессии b=0 или a=0 (незначимость коэффициентов регрессии) отвергается, если |t_факт|>|t_табл|, т.е. коэффициенты регрессии не случайно отклоняются от нуля и сформировались под влиянием систематически действующего фактора x.

10) Найдем с помощью функции СТЬЮДРАСПОБР (…) табличное значение по уровню значимости и числу степеней свободы .

11) Зная критические значения t_табл, можно найти границы доверительных интервалов для коэффициентов регрессии. Для этого находят предельные ошибки расчета для параметров регрессии:

; .

;

Рассчитаем доверительные интервалы для параметров регрессии:

, т.е. нижняя граница интервала параметра a: ;

верхняя граница интервала параметра a: .

, т.е. нижняя граница интервала параметра b: ;

верхняя граница интервала параметра b: .

Доверительные интервалы коэффициентов регрессии
a min=	-7349,34996	b min=	15,44472385
a max=	7349,854686	b max=	15,62633314

 

12) Прогнозное значение y_прогн определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x_прогн: .

млн. руб.

Стандартная ошибка индивидуального прогнозного значения:

Стандартная ошибка прогноза
	для y	962,7488142

 

Строится доверительный интервал прогноза:

, где

Доверительный интервал прогноза
	y min=	15298,90356
	y max=	19329,0164

 

Можно сделать вывод, что уравнение регрессии статистически значимо, расчетные значения F -статистик оказалось значительно больше критического уровня.

Вариация результата на 92,7% объясняется вариацией фактора x.

Связь весьма высокая, прямая.

Качество построенной модели оценивается как хорошее, т.к. не превышает 8 – 10%.

Коэффициент регрессии b значим, коэффициент регрессии а не значим.

 

	АНАЛИЗ МОДЕЛИ часть I	ВЫВОДЫ
	R квадрат	0,927052672
Ошибка аппроксимации	4,221837759	должна быть менее 8-10%
	корреляция	0,962835745
	Fфакт	241,4619054
	Fтабл	2,143834021	ЗНАЧ	Fфакт попадает / не попадает в область (Fтабл;+бесконечность)
t-статистика а факт	0,252361163	НЕЗНАЧ a
t-статистика b факт	15,53552849	ЗНАЧ b
	t табл	2,09302405	знач/незнач коэф-тов регр.	tфакт. попадает/не попадает в область (-бесконечность; t табл) и (t табл;+бесконечность)
Стандартные ошибки для коэффициентов
	для a	3511,475334
	для b	0,043384427
Доверительные интервалы коэф-тов регрессии
a min=	-7349,34996	b min=	15,44472385
a max=	7349,854686	b max=	15,62633314
Доходы ХМ АО
Хпрогн	24373,59048
Точечный
прогноз Y=	17313,95998		ожидаемая регрессия расходов в ХМ АО
Стандартная ошибка прогноза
	для y	962,7488142
Доверительный интервал прогноза
	y min=	15298,90356
	y max=	19329,0164

 

Рассчитаем параметры уравнений степеной парной регрессии:

1) С помощью мастера диаграмм Excel изобразим поле корреляции (зависимость y_i от x_i), выбрав тип диаграммы – ТОЧЕЧНАЯ.

 

 

2) Построим линию тренда степенного типа, которая Полученное уравнение вида: будет являться нелинейной регрессионной моделью зависимости потребительских расходов на душу населения и от уровня доходов населения на душу населения.

Линейное уравнение регрессии имеет вид .

3) Заполним таблицу, рассчитав значения Xi, Yi, XiYi, Xi².

№ п/п	Субъект РФ	СРЕДНЕДУ-ШЕВЫЕ ДЕНЕЖНЫЕ ДОХОДЫ2014 года (в месяц, руб)	ПОТРЕБИТЕЛЬСКИЕ РАСХОДЫв 2013 году В СРЕДНЕМ НА ДУШУ НАСЕЛЕНИЯ (в месяц, руб)	Линеаризованные переменные
x i	y i	Xi	Yi	XiYi	Xi2
	Белгородская область			4,3754	4,2068	18,4064	19,1440
	Брянская область			4,3043	4,1773	17,9803	18,5272
	Владимирская область			4,2741	4,1388	17,6894	18,2676
	Воронежская область			4,3435	4,2306	18,3757	18,8662
	Ивановская область			4,2582	4,1246	17,5634	18,1325
	Калужская область			4,3652	4,2007	18,3369	19,0545
	Костромская область			4,2449	4,0769	17,3060	18,0191
	Курская область			4,3183	4,1574	17,9528	18,6473
	Липецкая область			4,3468	4,2181	18,3351	18,8945
	Московская область			4,5151	4,3420	19,6045	20,3858
	Орловская область			4,2615	4,1161	17,5411	18,1608
	Рязанская область			4,2973	4,1288	17,7424	18,4666
	Смоленская область			4,3006	4,1571	17,8783	18,4955
	Тамбовская область			4,2974	4,1769	17,9499	18,4677
	Тверская область			4,2812	4,1571	17,7971	18,3284
	Тульская область			4,3202	4,1740	18,0326	18,6642
	Ярославская область			4,3248	4,1627	18,0028	18,7042
	Курская область			4,2451	4,0756	17,3012	18,0208
	Свердловская область			4,4915	4,3933	19,7328	20,1740
	Тюменская область			4,5611	4,3823	19,9882	20,8035
	Челябинская область			4,3402	4,2013	18,2347	18,8374
	Итого			91,0667	87,9984	381,7516	395,0621
	Среднее значение	22157,81	15823,905	4,3365	4,1904

 

 

4) Рассчитаем определители ∆, ∆ _С, ∆ _b с помощью функций: =МОПРЕД(C29:D30); =МОПРЕД(C34:D35); =МОПРЕД(C39:D40).

5) Определим параметры линеаризованной модели регрессии.

Y=C+b·X; ; .

Параметры линеаризованной модели
C=	-0,0070818
b=	0,967940429

 

6) Выполним потенцирование полученного уравнения регрессии и представим модель в виде степенной зависимости: .

 

 

Параметры степенной модели
a=	0,983825779
b=	0,967940429

 

 

Матрица коэффициентов системы нормальных уравнений для нахождения общего определителя:	Параметры линеаризованной модели
						C=	-0,0070818
			91,0667
		91,0667	395,0621			b=	0,967940429
∆=	3,159223504
Матрица коэффициентов системы нормальных уравнений для нахождения частного определителя ∆С:
		87,9984	91,0667
		381,7516	395,0621			Параметры степенной модели
∆С=	-0,022372995					a=	0,983825779
Матрица коэффициентов системы нормальных уравнений для нахождения частного определителя ∆b:
						b=	0,967940429
			87,9984
		91,0667	381,7516
∆b=	3,057940153

7) Заполним все колонки промежуточных расчетов таблицы, необходимые для дальнейшего анализа модели.

 

№ п/п	Квадраты отклонений фактора	Теоретические значения уравнения линеариз. регрессии	Общие квадраты отклонений результата	Квадраты отклонений, обусловленные регрессией (факторные/ объясненные регрессией)			Остаточные квадраты отклонения (случайные)
	(Xi-Xср) 2	Yi теор	(Yi-Yср)^2	(Yiтеор-Yср)^2	|Yi-Yiтеор|	|Yi-Yiтеор|/Yi	(Yi-Yiтеор)^2
	0,0015	4,2280	0,0003	0,0014	0,0212	0,0050	0,0005
	0,0010	4,1592	0,0002	0,0010	0,0180	0,0043	0,0003
	0,0039	4,1300	0,0027	0,0037	0,0088	0,0021	0,0001
	0,0000	4,1972	0,0016	0,0000	0,0334	0,0079	0,0011
	0,0061	4,1146	0,0043	0,0057	0,0099	0,0024	0,0001
	0,0008	4,2181	0,0001	0,0008	0,0174	0,0041	0,0003
	0,0084	4,1017	0,0129	0,0079	0,0248	0,0061	0,0006
	0,0003	4,1727	0,0011	0,0003	0,0153	0,0037	0,0002
	0,0001	4,2003	0,0008	0,0001	0,0177	0,0042	0,0003
	0,0319	4,3632	0,0230	0,0299	0,0212	0,0049	0,0004
	0,0056	4,1178	0,0055	0,0053	0,0017	0,0004	0,0000
	0,0015	4,1524	0,0038	0,0014	0,0237	0,0057	0,0006
	0,0013	4,1557	0,0011	0,0012	0,0014	0,0003	0,0000
	0,0015	4,1526	0,0002	0,0014	0,0243	0,0058	0,0006
	0,0031	4,1368	0,0011	0,0029	0,0202	0,0049	0,0004
	0,0003	4,1746	0,0003	0,0002	0,0006	0,0001	0,0000
	0,0001	4,1791	0,0008	0,0001	0,0164	0,0040	0,0003
	0,0084	4,1019	0,0132	0,0078	0,0263	0,0065	0,0007
	0,0240	4,3405	0,0412	0,0225	0,0529	0,0120	0,0028
	0,0504	4,4078	0,0368	0,0473	0,0255	0,0058	0,0006
	0,0000	4,1940	0,0001	0,0000	0,0074	0,0018	0,0001
Итого:	0,1504	87,9984	0,1510	0,1409	0,3884	0,0921	0,0100

8) Для анализа общего качества уравнения линейной формы регрессии определим коэффициент детерминации R².

.

R квадрат

0,933661

 

9)Коэффициент детерминации , т.е. в 93,4% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии – весьма высокая. Остальные 6,6% изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).

10) Рассчитаем ошибку аппроксимации , сформулируем вывод о качестве построенной модели:

 

.

Ошибка аппроксимации

1,849412

должна быть менее 8-10%

 

Качество построенной модели оценивается как хорошее, т.к. не превышает 8 – 10%.

10) Тесноту связи определяется с помощью коэффициента корреляции ρ_xy..

 

.

корреляция

0,966261

 

Связь весьма высокая, прямая.

11) значимость коэффициента детерминации R², исчислив F-критерий. Критическое (табл.) значение F-критерия определим с помощью встроенной функции «=FРАСПРОБР(α;m;n-m-1)».

,

где m – число параметров (коэффициентов) при X; n – число единиц совокупности

 

	Fфакт	267,4063
	Fтабл	4,38075	ЗНАЧ		Fфакт попадает в область (Fтабл;+бесконечность)

Расчетные значения F -статистик оказалось значительно больше критического уровня. Отсюда можно сделать вывод о наличии связи между анализируемыми факторами.

12) значимость коэффициентов для линеаризованной формы регрессии, используя t-критерии Стьюдента и . Критическое (табл.) значение t-критерия определим с помощью встроенной функции «=СТЬЮДРАСПОБР(α;n-m-1)».

 

;

 

 

t-статистика С факт

-0,37037

НЕЗНАЧ C

tфакт не попадает в область (-бесконечность;-t табл) и (t табл;+бесконечность)

t-статистика b факт

276,261

ЗНАЧ b

tфакт попадает в область (-бесконечность;-t табл) и (t табл;+бесконечность)

t табл

2,079614

 

Так как |t_{факт b}|>|t_табл|, то коэффициент регрессии b не случайно отклоняется от нуля и сформировался под влиянием систематически действующего фактора x.

Так как |t_{факт C}|<|t_табл|, то признается случайной природа формирования коэффициента регрессии C.

Зная критические значения t_табл, можно найти границы доверительных интервалов для коэффициентов регрессии. Для этого находят предельные ошибки расчета для параметров регрессии:

; .

;

13) Рассчитаем доверительные интервалы для параметров регрессии:

,

Доверительные интервалы коэф-тов регрессии
a min=	-7349,34996	b min=	15,44472385
a max=	7349,854686	b max=	15,62633314

 

Прогнозное значение y_прогн определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x_прогн:

млн. руб.

14) Стандартная ошибка индивидуального прогнозного значения:

С 95% вероятностью определим стандартную ошибку прогноза и доверительный интервал прогноза .

Средняя стандартная ошибка прогноза:

.

Стандартная ошибка прогноза
	для Y	0,023687

Доверительный интервал прогноза:

, где ;

Доверительный интервал прогноза
	Y min=	4,2155	y min=	16425,08
	Y max=	4,2629		18318,18
			y max=

Можно сделать вывод, что уравнение регрессии статистически значимо, расчетные значения F -статистик оказалось значительно больше критического уровня.

Вариация результата на 93,4% объясняется вариацией фактора x.

Связь весьма высокая, прямая.

Качество построенной модели оценивается как хорошее, т.к. не превышает 8 – 10%.

Коэффициент регрессии b значим, коэффициент регрессии C не значим.

 

 

АНАЛИЗ ЛИНЕАРИЗОВАННОЙ МОДЕЛИ часть I

ВЫВОДЫ

R квадрат

0,933661

Ошибка аппроксимации

1,849412

должна быть менее 8-10%

корреляция

0,966261

Fфакт

267,4063

Fтабл

4,38075

ЗНАЧ

Fфакт попадает в область (Fтабл;+бесконечность)

t-статистика С факт

-0,37037

НЕЗНАЧ C

tфакт не попадает в область (-бесконечность;-t табл) и (t табл;+бесконечность)

t-статистика b факт

276,261

ЗНАЧ b

tфакт попадает в область (-бесконечность;-t табл) и (t табл;+бесконечность)

t табл

2,079614

Стандартные ошибки для коэффициентов

для С

0,019121

для b

0,003504

Доверительные интервалы коэффициентов регрессии

С min=

-0,0468

b min=

0,9607

С max=

0,0327

b max=

0,9752

Доходы ХМ АО

Поделиться: