Глава ХI. Основы математической статистики
Основные понятия математической статистики
Математическая статистика занимается изучением закономерностей, которым подчинены массовые случайные явления. Пусть требуется оценить совокупность однородных объектов относительно некоторого качественного или количественного признака. Вся совокупность объектов, подлежащих оценке, называется генеральной совокупностью (ГС). При сплошном контроле обследуют каждый элемент ГС. Однако, сплошной контроль недопустим при больших объемах ГС или в случае его разрушительности. Основным методом математической статистики является выборочный. Выборочной совокупностью (ВС) или просто выборкой называют часть элементов ГС, отобранных для изучения требуемого признака. Объемом совокупности (ГС или ВС) называют число ее элементов. Выборка называется репрезентативной (представительной), если ее элементы относительно изучаемого признака правильно представляют всю ГС, т.е. их качественные характеристики близки. Для обеспечения репрезентативности выборки нужно, чтобы у каждого элемента ГС была одинаковая вероятность попасть в нее.
Пусть из ГС извлечена выборка объемом n. Затем исследуется количественный признак X ее элементов (длины деталей).
Возможные значения х1, х2, …, хn, количественного признака X называют вариантами. Последовательность вариант, записанная в возрастающем порядке, называется вариационным рядом. Величина |xmax - xmin| называется размахом выборки. Если значение x1 величины X наблюдалась n1 раз, значение x2 – n2 раза; значение xi – ni раз, то числа n1, n2, …, ni, … называют частотами, а их отношения к объему выборки 
- относительными частотами соответствующих вариант.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение удобно представлять в табличной форме.
Закон распределения вероятностей – перечень вариант и соответствующих им вероятностей.
Пример. В результате 10 опытов получена выборка 2,2,2,3,4,4,6,6,6,6. Написать для нее статистическое распределение выборки и закон распределения вероятей.
Статистическое распределение
х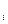 
| ||||
| n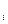
|
Закон распределения
| х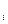
| ||||
| р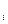
| 0,3 | 0,1 | 0,2 | 0,4 |
Полигоном частот называют ломаную, отрезки которой соединяют точки (xi, ni). Полигоном относительных частот называют ломаную, соединяющую точки (xi, wi).
В случае непрерывного признака или большого числа вариант целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов с шагом h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i – интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 
(плотность частоты). Площадь i-го частичного прямоугольника равна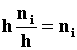 
- сумме частот вариант i – го интервала, а площадь гистограммы частот равна объему выборки. Площадь гистограммы относительных частот равна 1.
Генеральной или выборочной средними называют средние арифметические вариант соответствующих совокупностей:
; 
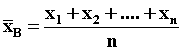. (11.1)
Здесь N, n – объемы соответственно ГС и ВС.
Генеральной или выборочной дисперсиями называют средние арифметические квадратов отклонений вариант от их средних:
; 
. (11.2)
Средним квадратичным отклонением называют квадратный корень из дисперсии:
; 
. (11.3)
Коэффициентом колеблемости случайной величины называют отношения:
; 
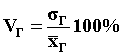. (11.4)
Стандартным отклонением или стандартной ошибкой среднего значения называют величину:
.
Доверительным интервалом для неизвестного параметра a некоторого распределения называется интервал L = (a - ε; a + ε), которому с данной вероятностью (надежностью) γ принадлежат все возможные значения этого параметра. Значение ε находят из формулы 
.
Эмпирическая функция распределения
В главе 10 шла речь о том, что все важнейшие характеристики случайной величины могут быть выражены в терминах ее функции распределения. В задачах математической статистики функция распределения (теоретическая) всегда является неизвестной. Замечательно то, что основываясь на выборке, можно построить хорошее приближение для неизвестной функции распределения F = F (t).
Пусть x = (x 1, …, x n) независимая выборка из неизвестного распределения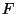 
.
Определение 11.1. Эмпирической функцией распределения 
называется функция :R ® [0; 1], вычисляемая по выборке x = (x 1, …, x n) следующим образом:
то есть, есть отношение числа элементов выборки, не превосходящих 
, к объему выборки.
Замечание 11.1. Слово ``эмпирическая'' в определении 11.1 означает, что функция вычисляется по данным опыта (эмпирическим данным), то есть, по выборке. По этой же причине для этого понятия иногда употребляют термин выборочная функция распределения.
Замечание 11.2. Легко видеть, что есть кусочно постоянная, неубывающая, непрерывная справа функция. Если все xi различны, то в каждой точке xi функция имеет скачок величины 
. Если какие-либо из xi совпадают, то соответствующие скачки суммируются.
Замечание 11.3. Как следует из определения 11.1, значение функции в точке зависит от выборки x = (x 1, …, x n), так что более полное обозначение для могло быть следующим: 
. В этом обозначении переменная является основной, а x 1, …, x n — фиксированные параметры. С другой стороны, x 1, …, x n интерпретируются как реализации независимых одинаково распределенных случайных величин с функцией распределения 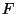. Таким образом, 
есть случайная величина.
Оказывается, что в пределе 
выборочная функция распределения равномерно сходится к теоретической:
|
Этот факт имеет общий характер и называется теоремой Гливенко. Ее доказательство выходит за рамки данного курса.
Гистограмма
Помимо эмпирических функций распределения, наглядное (но, вместе с тем, довольно приближенное) представление о неизвестном распределении можно получить при помощи гистограмм. Пусть x = (x 1, …, x n) — независимая выборка из неизвестного распределения 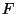. Выберем два числа 
и 
, -¥ < L < R < +¥, такими, чтобы все числа xi попали внутрь интервала (L; R]. Разобъем этот интервал на конечное число меньших интервалов:
где L = r 0 < r 1 < … < r m = R. Обозначим через 
длины интервалов разбиений. Теперь произведем, так называемую, группировку данных (выборки), а именно, для каждого интервала разбиения (r j-1; r j] объединим в группу те xi, которые попали в этот интервал. Пусть n j — число таких элементов выборки:
Определим функцию
График функции h (t)и называется гистограммой.
Таким образом, гистограмма представляет собой график кусочно-постоянной функции, такой, что площадь столбца с основанием, например, (r j-1; r j] равна частоте попадания измерений в этот интервал группировки. Вспоминая материал главы 10, можно заключить, что гистограмма является выборочным аналогом плотности распределения.
При построении гистограмм мы имеем свободу в выборе интервала (L; R], числа интервалов разбиения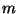 
и самих точек r 1, …, r m-1. Для получения хороших приближений для плотности неизвестного распределения следует всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по выбору этих параметров таковы.
- Значение 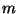должно быть существенно меньше, чем объем выборки
, но вместе с тем не слишком малым, чтобы гистограмма имела достаточно подробный профиль. - Интервалы разбиения следует выбирать так, чтобы каждый из них содержал ``достаточно много'' элементов выборки. Если в группах недостаточно большое число данных, то возможные случайные флуктуации их числа приводят к значительным искажениям реальной картины.
- При больших объемах выборки нередко берут разбиение интервала (L; R]на подинтервалы одинаковой длины.