19.
Момент силы- векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Направление вектора момента силы находим по правилу правого винта. Этот вектор 
и силе и радиус-вектору. 
; M=Fl;
Моме́нт и́мпульса- характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.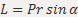 
=pl; Направление вектора L определяется по правилу правого винта.
20.
Момент инерции-произведение массы МТ на квадрат расстояния до оси вращения.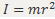 
; [I]=кг*м^2.
Теорема Штейнера-Момент инерции относительно произвольной оси вращения равен сумме момента инерции относительно параллельной оси вращения, проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями.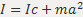 
, а-расстояние между осями.
Применение теоремы Штейнера:Для стержня: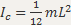 
Найдём момент инерции стержня относительно оси, проходящей через его конец: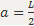 
, 
, 
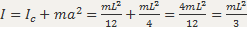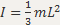
Для диска: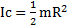 
, а=R,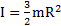 
21.
Работа при вращательном движении: 
; 
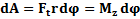; если 
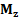=сonst, то 
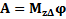-дифференциальное уравнение.
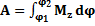-интегральное
22.
Кинетическая энергия вращения: Для каждой МТ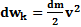 
= 
; 
; 
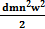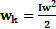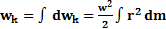
Кинетическая энергия для катящегося тела: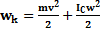 
23.
Основной закон динамики вращательного движения: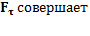 
работу 
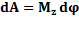, увеличивает кинетическую энергию вращающегося тела на 
. 
; 
; 
; 
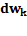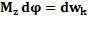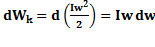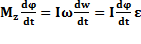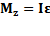. Если 
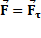, то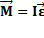 
-основной закон динамики вращательного движения.
24.
Гармонические колебания- происходят по закону синуса или косинуса, формула (Кинематическое уравнение гармонических колебаний):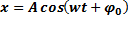 
, х-значение колеблющейся величины в момент времени t.
Характеристики гармонических колебаний: А-амплитуда колебаний;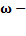 
циклическая частота, 
; 
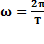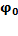-начальная фаза колебаний;
Величина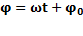 
-это фаза колебаний. Именно она определяет значение ‘х’ в данный момент времени.
Скорость и ускорение при гармонических колебаниях:
Пусть МТ совершает колебания вдоль оси х, тогда: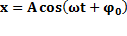 
; 
; 
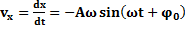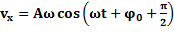. Скорость опережает координату на 
.
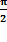Амплитуда скорости-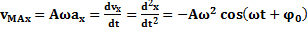 
; 
; 
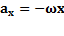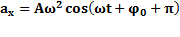. Ускорение опережает координату по фазе на 
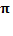рад.
Амплитуда ускорения-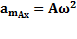 
25.
Пружинный маятник-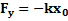 
; 
;
; 
; 
; 
.
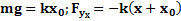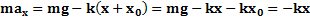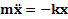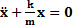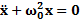Для пружинного маятника: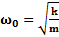 
, 
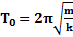
Математический маятник-частный случай физического. Тело подвешено на нити, можно считать МТ.
Для математического маятника: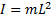 
; 
; 
; 
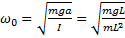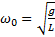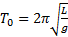
26.
Физический маятник-Это тело, совершающее под действием силы тяжести колебания, вокруг горизонтальной оси, не проходящий через его центр масс.
Потенциальная энергия: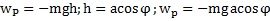 
Кинетическая Энергия: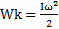 
.
Полная Энергия: 
Для физического маятника: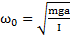 
; 
.
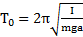27.
Уравнение затухающих колебаний:
Пусть на маятник массой m, кроме квазиупругой силы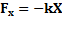 
, действует сила сопротивления 
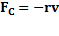, r- коэффициент сопротивления, тогда 
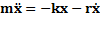. Делим на массу: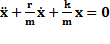 
Обозначим: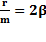 
, 
. 
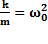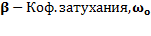-собственная циклическая частота.
Уравнение движения примет вид: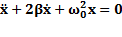 
-Дифференциальное уравнение затухающих колебаний. Его решение: 
- 
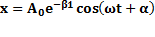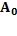-начальная амплитуда, 
-начальная фаза колебаний,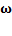 
-циклическая частота затухающих колебаний: 
; 
.
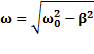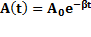1)Время релаксации 
-время, за которое амплитуда колебаний уменьшается в ‘e’ раз 
, 
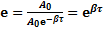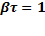или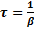 
, 
.
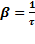2)Логорифмический декремент затуханий-натуральный логорифм отношения амплитуды, взятых через период.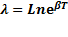 
, 
, 
= 
, 
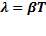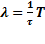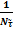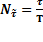-число колебаний за время 
3) Добротность-колебаний системы Q пропорциональна отношению энергии системы в данный момент времени к убыли энергии за период колебаний.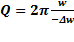 
28.
Вынужденные колебания-происходят под действием периодической внешней силы.
Добавим в уравнение движения периодическую силу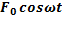 
, 
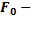амплитуда, 
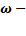циклическая частота внешних воздействий. 
, 
, 
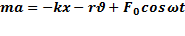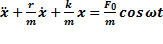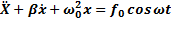-дифференциальное уравнение вынужденного колебания.
Если есть затухания (всегда), то амплитуда колебаний резко возрастает при некоторой частоте внешнего воздействия, уже не равной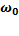 
-это явление называется РЕЗОНАНС.
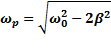
29.