Классификация ДУЧП I (первого порядка)

Df ДУЧП I называется линейным, если неизвестная функция и её частные производные входят в уравнение линейно. Такое ДУ имеет вид:

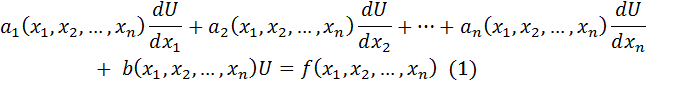
Если функция , то уравнение (1) называется однородным.

В уравнении (1)коэффициенты не содержат искомой функции . Если они, кроме независимых переменных , зависят ещё и от , то такое ДУЧП I называется квазилинейным.

Вопрос 31. Системы ДУ в симметрической форме. Интегрирование линейных и квазилинейных ДУ первого порядка с частными производными. Первые интегралы и интегрируемые комбинации.

Интегрирование линейных и квазилинейных ДУЧП I

a) Интегрирование линейных уравнений

Рассмотрим уравнение вида:

где , а – известные функции независимых переменных , определенных в области , непрерывные и непрерывно дифференцируемые в некоторой окрестности т. и одновременно не обращающиеся в 0.

Будем считать, что в этой точке, а – искомая функция.

Уравнение (1) будем называть линейное однородное ДУЧП I.

Df Решением уравнения (1) называют дифференцируемую функцию от , при подстановке которой в (1) оно становится тождеством. Геометрически такое решение можно интегрировать как поверхность в пространстве
ⁿ⁺¹, т.е. . Такую поверхность называют интегральной.

Очевидным решением уравнения (1) является решение U=C, С – постоянная.

Наряду с уравнением (1) будем рассматривать соответствующую ему систему вида:

где – те же функции, как и в (1).

Система (2) называется системой обыкновенных ДУ в симметрической форме, соответствующей уравнению (1). Систему (2) называют также характеристическим для уравнения (1), а её решения называются характеристиками этого уравнения. В силу условий, налагаемых на коэффициенты уравнения (1), систему (2) можно записать в нормальной форме:

В общем случае система (3) может иметь n-1 независимых решений. Пусть:

…

Каждое из уравнений (4) называется первым интегралом системы (3), а каждая из функций

называется интегралом этой системы.

Связь между решением уравнения (1) и интегралами соответствующей системы в симметрической форме (2) или (3) установим следующими теоремами:

Теорема 1: Если – интеграл системы (2) или (3), то функция является решением уравнения (1).

Доказательство:

Пусть является интегралом системы (3), тогда является первым интегралом этой системы. Это значит, что полный дифференциал данной функции в силу системы (3) равен 0, т.е. . Воспользуемся Df полного дифференциала функции. Имеем:

Подставляя в эту формулу выражения , полученные из системы (3), находим:

, т.к. выражение в скобках тождественно равно 0. ЧТД.

Теорема 2: Если является решением уравнения (1), то – интеграл систем (2), (3). (Доказательство аналогично предыдущему)

Теорема 3 (об общем решении системы (1)): Пусть являются независимыми интегралами системы (2) или (3). Тогда функция 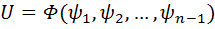является общим решением уравнения (1), где – любая функция имеющая непрерывные производные по . (без доказательств)

b) Интегрирование квазилинейного ДУЧП I.

Запишем такое уравнение вида:

Где – определенные непрерывные функции вместе со своими частными производными в некоторой окрестности т. .

Уравнение (5) отличается от линейного уравнения (1) тем, что коэффициенты от могут зависеть от неизвестной функции U. Интегрирование квазилинейного уравнения (5) можно свести к интегрированию вспомогательного однородного уравнения I порядка вида:

где является неизвестной функцией аргументов

Как указано ранее, интегрирование уравнения (6) сводится к нахождению интегралов в соответствующей системе в симметрической форме, т.е.:

Если являются независимыми интегралами системы (7), то решение функционального ур-ния является общим решением ур-ния (5), т.к. зависит от производной.

Вопрос 32. Характеристики и интегральные поверхности

Укажем связь между характеристиками и интегральными кривыми уравнения:

И системы 2 в симметрической форме. Рассмотрим этот случай на примере ДУ, зависящего от 2ух независимых переменных (12)

Коэффициенты в (12) задают в 3-ёхмерном пр-ве векторное поле.

, где р – точка в , p=(x,y,z).

Если такая т.р лежит на интегральной поверхности S: z=z(x,y), то вектор , направлен по нормам к поверхности S в т. р. Тогда ур-ние (12) можно записать в виде: , причём =0, т.е. векторы ортогональны. Из сказанного следует: вектор лежит в касательной пл-ти к интегральной поверхности. Справедливо обратное:

2)Если поверхности S: z=z(x,y) в каждой своей точке р касается вектора , то S является интегральной поверхностью. Т.к. характеристика и интегральная поверхность, проходящая через точку р, касается вектора , то интегральная поверхность расслаивается на характеристики:

Теорема. Если интегральная поверхность S содержит точку , то она содержит и характеристику, проходящую через эту точку.

Док-во: Рассм. Систему; , где х=z(x,y) и поставим задачу Коши: . Пусть функции x(t) и y(t) – решения этой задачи. Кривая Г, определённая параметрически: Г: лежит на интегральной поверхности. Покажем, что Г явл. характеристикой: Имеем 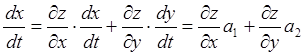, т.к. ф-ция z=z(x,y) – решение (12) ч.т.д.

Пример.

Характеристики этой системы имеют 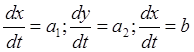. Откуда получаем, что характеристиками являются кривые: , Получим, что такие характеристики образуют семейство прямых, параллельных вектору , а это значит что интегральными явл. цилиндрические пов-ти, образующие которых параллельны вектору . 1-ые интегралы: =>

общее решение имеет вид Ф()=0

Вопрос 33. Задача Коши для лин-ых и квазилинейных ДУ 1-го порядка с частными производными

Пусть дано уравнение (1). Зададим для этого ур-ния начальные условия (8))т.е. решим задачу Коши для этого уравнения. Пусть - система независимых интегралов (система характеристик для системы (2) в симметрической форме), тогда общее решение уравнения (1), как указывалось ранее имеет вид: .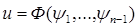

И для выполнения начального условия (8) ф-ции Ф надо подобрать так, чтобы выполнялось равенство: .

Из данного равенства образуем систему функциональных уравнений: (9)

Разрешая уравнение системы (9) через . Получим (10), где

Пусть далее Ф( = . При таком определении функции Ф равенство u=Ф(). Функция и является решением уравнения (1), которая удовлетворяет начальному условию (8), т.е. u=

Исходя из изложенного выше решение задачи Коши для уравнения (1) с начальными условиями (8) производится по следующей схеме.

1) Находим независимые интегралы системы в симметрической форме

2) Составляем систему функциональных уравнений (9), которые разрешаем относительно

3) Строим ф-ции Ф по ф-лам (10)

4) Записываем искомое решение по ф-ле (11)

Вопрос 34. Линейные и нелинейные волны

Рассмотрим поведение з.Коши для линейных и квазилинейных ур-ний, отметим, что эти решения существенно различны, не смотря на то, что по виду такие ур-ния похожи друг на друга. Рассм. Линейное ур-ние: (1), где С-const, а так же квазилинейное ур-ние (2).

Зададим для этих ур-ний одни и те же начальные условия: (3), где f(x) – гладкая =0 вне некоторого отрезка ф-ция. Любое решение ур-ния (1) имеет вид: u=Ф(x-Ct) (4). Решение з. Коши для этого ур-ния имеет вид: u(x,t)=f(x-Ct) (5). Постоянная С в этом ур-нии имеет размерность скорости, т.е. является скоростью распространения возмещений. График ф-ции получается из графика ф-ции f(x) сдвигом на расстояние Ct => ф-ция и геометрически и физически представляет волну, бегущую на право со скоростью С. Получим, что решение з. Коши для ур-ния (1) явл. непрерывая, бегущая волна. Аналогичный результат, когда С(x,t) – нерешенная. Любое решение ур-ния (2) даётся ф-лой: Ф(u,x-tu)=0. Будем считать, что это решение разрешимо относительно u т.е. u=F(). Проведём качественную картину распространения волны в этом случае: значение u - скорость движения волны в т.С . В начальный момент при t=0 эта скорость будет макс-ой в точке р на гребне волны. В последующие моменты времени точки на профиле волны, лежащие левее вершины р будут отставать от р, а точка р будет «догонять» точки профеля лежащие правее => Задний фронт волны будет становиться более крутым. Наконец, в некоторый момент на переднем фронте появится точка с вертикальной касательной. В последующем, при увеличении времени ф-ция u(x,t) станет неоднозначной. Неоднозначная ф-ция не имеет физического смысла для некоторых задач, например в задачах газовой динамики. Физические соображения приводят к необходимости рассмотрения при разрывного решения ур-ния (график на рис. Выше) Положение разрыва определяется по правилу площадей: заштрихованные площади равны. Такое разрывное решение ур-ния (2) наз. Ударной волной.