Df Положительно определенная в окрестности U т. – u 
= 
функция V(
) называется функцией Ляпунова системы (1), если V′ (
) ≤0, 
U.
Здесь символ V′ () называется производной функции V() в силу системы (1). Это значит, что V′ ()= 
Теоремы Ляпунова об устойчивости, асимптотической устойчивости и неустойчивости.
Пункт А. Теорема Ляпунова об устойчивости.
Теорема. Если для системы(1) 
в области U, т.е. в окрестности положения равновесия знакоопределенная функция V(
), производная которой по времени V′ (
) взятая в силы системы(1) является знакопостоянной функцией знака противоположного знаку функции V(
), то положение равновесия 
устойчиво в смысле Ляпунова (утойчиво по Ляпунову).
Другая формулировка теоремы Ляпунова об устойчивости. Если в некоторой окрестности U положение равновесия 
функция Ляпунова V(), то это положение равновесия устойчиво по Ляпунову.
Доказательство: Пусть состояние равновесия является начало координат, т.е. т. 
. Выберем число 
> 0, так чтобы шар K 
, такой что | 
|< 
лежал в окрестности U т... 
=О
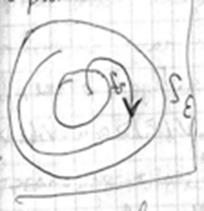
Пусть S 
является границей шара K 
, т.е. это сфера радиуса 
или | |= 
, т.к. S 
- замкнутое ограниченное мн. функция V() – непрерывна в нем и положительна на S 
(т.е. V() >0 на S ), то минимальное значение функции V(
) =K>0.
Рассмотрим шар K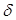 
, такой что | 
| 
и пусть этот шар содержится в U. Т.к. V(
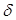)=0, то величину >0 можно выбрать так, чтобы выполнялось неравенство V() <K при K 
Такой выбор 
можно сделать в силу непрерывности функции V(
). Покажем, что если | 
|< 
, то |x(t, 
)|< 
для любого t 
[0;∞). Ч.Т.Д,
Т.к. V′ () 
0, следовательно V() – функция Ляпунова в U и V(
<K., то V()<K, V [0; ∞).
Причем, последнее неравенство выполняется??? фазовой траектории 
= 
(t, ), а это значит, что траектория, которая начинается в шаре K не может пересечь границы K 
, т. к. V()<K на траектории и V(
)=K на S 
.
Пункт Б Теорема Ляпунова об асимптотической устойчивости.
Теорема. Если для системы (1) 
знакоопределенная функция V(
) полная производная которой по времени найдена в силу системы (1) является также знакоопределенной, знакопротивоположной с V(), то положение равновесия асимптотически устойчиво(устойчиво по Ляпунову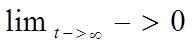 
).
Другая формулировка: пусть в некоторой окрестности U положение равновесия 
функция Ляпунова V(
), такая что V′ (
) в силу системы (1) является отрицательно-определенной в U, тогда положения равновесия 
ассимптотически устойчивой.
Без доказательства.
Пункт В. Теорема Ляпунова о неустойчивости.
Если функция V(), имеющая знакоопределенную V′ () и такая, что в V окрестности U т. – и 
, функция V′ () не является знакопостоянной, знакопротивоположно с V(), то положение равновесия не устойчиво.
Теорема Читаева о неустойчивости. Пусть функция V(
) непрерывно диффиренцируема в области U1 
U, V()>0 и V′ (
) >0, где 
U1и кроме того V(
)=0 в тех точках области U1, которые лежат внутри области U и явл. граничными для области U1, тогда положение равновесия 
не устойчиво.
Вопрос 27. Рассмотрим линейную однородную систему записанную в векторной форме 
(1),где матрица А образована из пост действительных или комплексных чисем. Очевидно (1) имеет состояние равновесия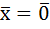 
. Для дальнейшего рассуждения сформулируем теорему о приведении м А к почти диагональному виду.
Т. Всякую квадратную матрицу порядка n можно привести к почти диаг виду, т.е. существует м. Т такая, что 
АТ=Л+ 
, где Л-диаг м., элементами которой явл все собственные значения м. А, а ядля элем 
м. имеет место оценка 
< 
, где положительное число 
можно выбрать сколь угодно малым
Т.Положение равновесия 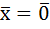сист (1) асимптотически устойчиво тогда и только тогда, когда действительные части всех собственных значений м.А явл. отрицательными.
След1: Если среди корней характеристического уравнения есть хотя бы один с положительной действительной частью, то нулевое решение системы (1) не устойчиво.
След2:Если характеристическое уравн сист (1) не имеет корней с положительной действительной частью, но имеется ряд корней с нулевой положительной частью, то может иметь место нач. устойчивость (но не асимптотическая) так и неустойчивость нулевого решения этой системы.
Критерий Рауса-Гурвица:
Дано уравнение (1) записано характеристическое ур. (2) 
= 
+ 
+..+ 
+ 
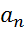=0
Будем считать, что коэф- действительные числа. Из коэф мн-на (2) составим матрицу:
А= 
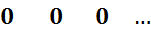
Члены с инд. > чем n и < 0 =0
Образуем диаг. Определ из диагональной матрицы:
= 
= 
…
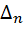=detA, т.к. последняя строка все нули кроме 
, то 
= 
Т(критерий Рауса-Гурвица)
Для того, чтобы все корни ур.(2) имели отрицательные действительные части необходимо и достаточно, чтобы выполнялись неравенства:
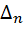>0 k=1,n
Пример для квадратного уравн 
+ 
+ 
=0
Этот критерий имеет вид 
>0,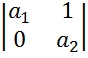 
>0 следовательно 
Пример для уравн 3ого порядка 
+ 
+ 
=0
>0 
, >0, >0, 
Вопрос 28. Рассмотрим сист. 
(1), 
- дважды непрер-диф в некоторой окр. U т. 
. Разложим вектор ф-ции 
по ф-ле Тейлора = 
()(
)+ 
(2)
Если т 
, 
достаточно близки, т.е.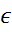 
U т (), то 
()()+
Отбросив в (2) не лин. Члены получим систему 
(3), где 
, А=f ()
Сист (3) наз линеаризованной для сист (1) в окр состояния т
Переход от не линейной системы (1) к лин. Системе (3) наз линеаризацией сист (1). При этом линеаризов. сист- это система линейная с пост коэф.Эта система интегрируется и поэтому устойчивость положения равновесия 
легко находится.
Покажем, что по структуре положения равновесия очень часто можно судить судить об устойчивости линейных ситсем вида (1)
Т Ляпунова об устойчивости по лин приближению:
Если положение равновесия линеаризироной системы асимптотически устойчиво, то положение равновесия не линейной системы также асимптотически устойчиво.
Неустойчивость по линейному приближению:
Т. Пусть дважды непрер диф в некоторой окрестности положения равновесия ,если м. Якоби имеет собственные значения с положительной действительной частью, то положение равновесия не устойчиво.
Вопрос 29. Предположим, что при линеаризации получим однородную лин сист вида
, где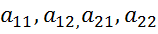 
-действительные числа
Пусть x= 
, y=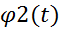 
действительное решение системы, тогда ур. x= 
, y= 
определена кривой на плоскости XOY, эта кривая наз. Фазовой траекторией системы (1). А картина, которая образует фазовую траекторию системы (1) наз. фаз. портретом этой сист. Одной из фазовых траекторий сист (1) 
, 
следует,что фазовая траектория система явл точкой с коорд (0,0). Такая точка наз точкой покоя или состоянием равновелия сист(1). Как известно сист. (1) легко интегрируется а следовательно можно построить фазовый портрет этой системы, который опред в зависимости от знач корней характер уравн. Пусть 
, 
явл корнями характер уравн вида 
=0 корни такого уравн наз собственными значениями матрицы А. Поскольку коэф при неизвестных сист (1) действительные числа, поэтому возможны 2а варианта:
1) Корни , -действит
2) , -корни сопряж
Пусть оба корня действит: тогда собственные вектора можно взять действительными, а тогда всякое решение системы имеет вид x(t)= 
+ 
(2), 
- произвольн пост, а x(t) имеет координаты (x(t), y(t)). Векторы 
образуют базис на плоскости. Пусть 
, 
координаты вектора x(t) в этом базисе, т.е. 
, 
(3)
Рассмотрим несколько случаев зависящих от знака корней характер уравн:
1) , -действит одного знака <0
Если 
, 
то фазовой траекторией явл ось 
В результате получим портрет, такое сост равновесия наз устойчивым узлом. α= 
следует, что фазовые траектории имеют вид парабол
2) Пусть , >0. Фазовый портрет такой же как описано выше, только стрелки в другом направлении.Такое положение равновесия наз неустойчивым узлом
3) 
, <0. Если 
то имеем 
, 
= 
, при t 
∞, а если 
, то имеем 
, 
∞, при t 
∞. Еще два луча получ, если 
,
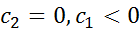. В результате траекторией системы (1) явл 4е луча. 2а из которых примыкают к т (0,0) при t ∞,а 2а других выходят из этой точки, при t ∞.Или можно сказать входят в нач координат при t 
∞. 2а луча наз. Сепаратрисами седла, т.к. положение равновесия в этом случ наз седлом. Если , и траектория имеет вид гипербалоида. Такое сост наз седлом.
Положение седло всегда неустойчиво.
4) , - компл корни
, тогда всякое реш сист (1) имеет вид (2), а всякое действительное решение сист (1) имеет вид 
+ 
(4)
Пусть 
, 
= 
, c=a+bi, 
Будем считать, что 
, 
-действит, тогда 
.Если оба корня чисто мнимые, т.е. 
, 
, следует, что фазовая траектория явл элиплом, Направление обхода зависит от знака 
.Если 
, то обход против часовой стрелки:
Нач координат явл устойчивым полож равновесия, но не ассимптотич.
Пусть 
, то траектория сист (1) явл спиралями, коротые закругляются в нач координат при t ∞.Такое положение равновелия наз устойчивый фокус, если 
, только направл движ меняется на противоположное. Такое положение равновесия наз неустойчивым фокусом.
Вопрос 30. Некоторые задачи, приводящие к уравнениям первого порядка с частными производными.
a) Уравнение поверхностей
Рассмотрим в некотором пространстве поверхность 
, образованную вращением около оси 
кривой 
, расположенной в плоскости 
. Уравнение этой поверхности имеет вид 
(1), где 
– достаточно гладкая функция. Продифференцируем (1) по 
и по 
. Получим:
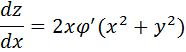
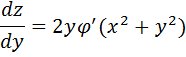
или 
(2)
Получим уравнение, содержащее 4 производные первого порядка относительно неизвестной функции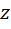 
. Графиком решения является поверхность 
в трехмерном пространстве 
, и эта поверхность называется интегральной поверхностью уравнения (2).
b) Рассмотрим функцию вида:
, где 
- постоянная, 
- время, - пространственная координата.
Её график в момент времени получается из графика функции в момент времени 
со сдвигом на расстояние 
вдоль 
есть волна, бегущая вдоль 
со скоростью . Т.к. 
и 
, то функция 
удовлетворяет ДУЧП:
