Геометрическая интерпретация ДУ 1порядка
Такие отрезки наз. направлениями данного ДУ. ДУ  определяет в области поле направлений. Пусть
определяет в области поле направлений. Пусть 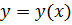 есть интегральная кривая ДУ
есть интегральная кривая ДУ  . Если эта кривая проходит через т.-у
. Если эта кривая проходит через т.-у 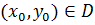 , то очевидно
, то очевидно  и
и  . Следовательно, интегральная кривая в т.-е
. Следовательно, интегральная кривая в т.-е  касается направления уравнения, и наоборот, если кривая
касается направления уравнения, и наоборот, если кривая 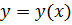 находится в области D и в каждой т.-е
находится в области D и в каждой т.-е  она касается направления данного уравнения, то
она касается направления данного уравнения, то  , а значит,
, а значит,  явл. интегральной кривой этого ур-ния. Поэтому проинтегрировать ДУ
явл. интегральной кривой этого ур-ния. Поэтому проинтегрировать ДУ  в области D, значит найти в этой области все кривые, которые в каждой т.-е касаются направления уравнения.
в области D, значит найти в этой области все кривые, которые в каждой т.-е касаются направления уравнения.
Вопрос 3. Обратная задача интегрирования ДУ. Интегрируемость в квадратурах в замкнутом виде.
Найти ДУ для которого ур-ние  определяет общее решение. Дифференцируем его:
определяет общее решение. Дифференцируем его: 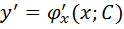 ;
; 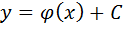
Теорема о неявном переходе:  и
и  -искомое ДУ.
-искомое ДУ.
Процесс нахождения решения ДУ наз. интегрированием этого ДУ. Если при этом удается выразить все решения в элементарных ф-циях, то говорят, что ур-ние проинтегрировано в элементарных ф-циях. Если ур-ние не интегрируется в элементарных ф-циях, но все его решения выражаются через неопределенные интегралы от элементарных ф-ций, то говорят, что уравнение проинтегрировано в квадратурах. Квадратурой наз. операция взятия неопределённого интеграла.
Если уравнение удается проинтегрировать в элементарных ф-циях или в квадратурах, то говорят, что оно интегрируемо в конечном виде.
Вопрос 4. ДУ с разделяющимися переменными. ДУ  , которое можно записать в виде:
, которое можно записать в виде: 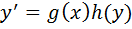 , где g(x) и h(x)-ф-ции, определенные на интервалах (a,b) и (c,d) соответственно, наз. уравнением с разделяющимися переменными.
, где g(x) и h(x)-ф-ции, определенные на интервалах (a,b) и (c,d) соответственно, наз. уравнением с разделяющимися переменными.
Ур-ние c разделяющимися переменными 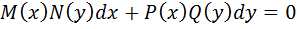 где
где  относительно своих аргументов.
относительно своих аргументов. 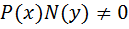
ДУ с разделёнными переменными 
Если ф-ции g(x) и h(y) непрерывны на интервалах (a,b) и (c,d) соответственно и при этом  для каждого
для каждого 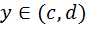 , то интеграл ДУ с разделяющимися переменными вычисляется по ф-е:
, то интеграл ДУ с разделяющимися переменными вычисляется по ф-е: 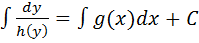 , где С-произвольная постоянная.
, где С-произвольная постоянная.
Теорема( 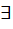 и! решения задачи Коши) Если ф-ции g(x)и h(y)непрерывны на интервалах (a,b)и(c,d) соответственно и при этом
и! решения задачи Коши) Если ф-ции g(x)и h(y)непрерывны на интервалах (a,b)и(c,d) соответственно и при этом  для любого
для любого 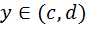 , а также если
, а также если  ,
,  , то задача Коши
, то задача Коши  имеет только одно решение.
имеет только одно решение.
Уравнение вида 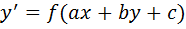 приводятся к уравнению с разделяющимися переменными заменой
приводятся к уравнению с разделяющимися переменными заменой  , с=const.
, с=const.
Вопрос 5. Однородные уравнения и уравнения, приводящиеся к ним. Геометрические свойства семейства интегральных кривых.
ДУ  наз. однородным, если в нем ф-ции M(x,y) и N(x,y), определенные в области D, явл. однородными одной и той же степени. Это уравнение приводиться к виду
наз. однородным, если в нем ф-ции M(x,y) и N(x,y), определенные в области D, явл. однородными одной и той же степени. Это уравнение приводиться к виду  .
.
Как решать:
а)замена переменных y=ux, которая приводит к уравнению с разделяющимися переменными вида 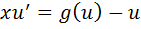 , где
, где 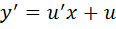 .
.
в)замена 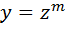 , где m вычисляется после замены, т.к. степени всех его членов должны быть равны между собой.
, где m вычисляется после замены, т.к. степени всех его членов должны быть равны между собой.
Теорема(  и! решения задачи Коши) Если ф-ция g(x) непрерывна на интервале (a,b)и удовлетворяет условию
и! решения задачи Коши) Если ф-ция g(x) непрерывна на интервале (a,b)и удовлетворяет условию  , то задача Коши
, то задача Коши  ,
, 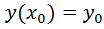 , где
, где  , имеет только одно решение.
, имеет только одно решение.
Уравнения, приводящиеся к однородным.
 -не явл. однородным
-не явл. однородным 
Потребуем 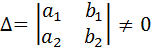 (1), для системы
(1), для системы 
 решение. Пусть
решение. Пусть  -решение. Введём замену
-решение. Введём замену  ,где
,где  - числа, т.к.
- числа, т.к.  -числа. Х-старая независимая переменная, а
-числа. Х-старая независимая переменная, а 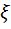 - новая. У-старая искомая ф-ция, а -новая. Подставим замену в начальное уравнение:
- новая. У-старая искомая ф-ция, а -новая. Подставим замену в начальное уравнение: 
Пусть(1) не выполняется: а) 
б) 
Замечание. Ур-ние  , где f-некоторая ф-ция, всегда могут быть проинтегрированы в квадратурах.
, где f-некоторая ф-ция, всегда могут быть проинтегрированы в квадратурах.